Diskussion:Corioliskraft/Archiv/1
Einfluss auf Kranlasten
Den Abschnitt mit dem Kran halte ich als Physiker für falsch. Erstens ist die radiale Geschwindigkeit des Kranauslegers sehr klein (etwa 1m/s), zweitens hängt es natürlich von der Orientierung des Krans ab (maximal in N/S Richtung, verschwindend in O/W Richtung. Jedes Lüftchen dürfte den Effekt überdecken. --Schweikhardt
- Ich glaube, damit ist der Kran selbst gemeint, der sich dreht. Wenn der Kranführer zusätzlich den Ausleger zum Beispiel nach innen bewegt, wirkt eine Corioliskraft, die das hängende Objekt in Drehrichtung auslenkt. Dies erstaunt einen unerfahrenen Kranführer wahrscheinlich schon. Die Erdrotation spielt hier natürlich keine Rolle, ebensowenig wie die geografische Orientierung. --Hubi 08:39, 23. Mär 2005 (CET)
- Da empfiehlt sich meines erachtens das Nachrechnen und ich befürchte auch das die Corioliskraft auf derartige Dinge einen verschwindend geringen Einfluss hat. Siehe das berühmte Badewannenabflussbeispiel. Ein massiver Kran bei geringen Geschwindigkeiten und ein Wind mit in großen Höhenlagen weit über 100 km/h sind gaaaannnz andere Größenordnungen. Ich würde mich da strickt an abstrackte Modelle beim Erklären oder Anwendungsbeispiele mit Winden halten. Alles ander führt nur zu Missverständnissen. Zeit hatte ich für den Artikel noch nicht, aber ein Leser sollte ihn eigentlich mit der Erkenntnis verlassen können, dass man mit der Corioliskraft nicht erklären kann, wie/warum sich der Abflusswirbel dreht oder wo der Äquator liegt. Über letzteres könnte man auch noch etwas schreiben, denn es gibt tatsächlich Leute, die mit einem (gezinkten) Abfluss den Äquator auf ihr Grundstück genau bestimmen wollen und dabei (sic!) auch regelmäßig fürs Fernsehen gefilmt werden. --Saperaud (Disk.) 12:45, 23. Mär 2005 (CET)
- PS: Wäre es nicht besser die Corioliskraft mit der Winkelgeschwindigkeit zu definieren anstatt mit de Kreisfrequenz? Dumm ist auch das beide die gleichen Formelzeichen haben. Kennt jemand vielleicht ein anderes nutzbares Formelzeichen für die Kreisfrequenz um die Verwechslungsgefahr einzuschränken? --Saperaud (Disk.) 13:08, 23. Mär 2005 (CET)
- Wenn der Kran sich in 30 s ganz rum drehen kann und der Ausleger sich mit 1 m/s bewegen lässt, so ist die Coriolisbeschleunigung 2*2π/30s*(1 m/s), also ungefähr 0,42 m/s2. Mit der Erdbeschleunigung von 9,81 m/s ergibt das eine Auslenkung der hängenden Last von 360°/2π*arctan(0,42/9,81)=2,4 Grad (wenn ich nicht irre, bin leider raus aus dem Berechnen von solchen Aufgaben). Das dürfte kaum genügen, also muss das Kranbeispiel raus. N/S und O/W oben haben natürlich weiterhin nichts mit dem Kran zu tun. --Hubi 20:08, 23. Mär 2005 (CET)
- Allerdings kann mE bei 2,4 Grad nicht gerade von verschwindend geringem Einfluss gesprochen werden. Das ist nahe an der Grenze, bei der man's in der Praxis wirklich berücksichtigen muss. --Hubi 07:59, 24. Mär 2005 (CET)
- Winkelgeschwindigkeit und Kreisfrequenz sind meines Erachtens doch identisch, solange der Winkel im Bogenmaß angegeben wird?! Eine ganze Umdrehung entspricht im Bogenmass Δφ=2π (Umfang des Einheitskreises), wird hierzu die Zeit t benötigt, so ist die Winkelgeschwindigkeit ω=Δφ/t = 2π/t. Für die Kreisfrequenz erhält man mit f=1/t das Ergebnis ω=2πf=2π/t. Die ω's sind also identisch, dasselbe Formelzeichen also gerechtfertigt! --Hubi 08:12, 24. Mär 2005 (CET)
Nochn Link
Folgender Link enthält einige sehr ausführliche und intersannte Sichtweisen auf die Corioliskraft: [1]. Wenn's interessant genug erscheint könnte man ihn ja verlinken und somit recht unwegredbar einem der verbreitesten Irrtümer in Bezug auf die Wirkung der Corioliskraft Paroli bieten. --Saperaud 20:29, 16. Dez 2004 (CET)
Richtung der Wirbelstürme
Hallo,
ich habe mal eine Frage. Ist das sicher, dass der Wirbelsturm sich auf der Nordhalbkugel gegen den Uhrzeigersinn dreht? Ich dachte die Luftmassen bewegen sich vom Äquator Richtung Norden, so dass in den oberen Gefilden auf Grund der Coriolis Kraft Richtung Osten die Luft sich eher dann im Uhrzeigersinn dreht. (siehe u.a. Jetstream. Oder wo ist mein Denkfehler? --Epikur 02:11, 23. Sep 2004 (CEST)
- Wirbelstürme sind Tiefdruckgebiete, die Luft strömt von der Umgebung Richtung Zentrum des Wirbelsturms. Dabei wird es auf der Nordhalbkugel nach rechts - also im Uhrzeigersinn - abgelenkt, dadurch bewegt sich die Luft rechts am Zentrum vorbei, wird aber durch den Unterdruck Richtung Zentrum gezogen, und der ganze Wirbelsturm dreht sich also im Gegenuhrzeigersinn. 193.171.121.30 16:06, 4. Okt 2004 (CEST)
Das verstehe ich nicht. Nach Lektüre des Artikels hielt ich für einleuchtend, dass Bewegungen auf der Nordhalbkugel eine Scheinrotation gegen den Uhrzeigersinn vollführen. Aber: Sind die Kreisel auf dem Globusbild dann nicht falsch herum? wb 22.09.05
Im Text steht was von wegen Luft strömt unten in ein Tief ein und oben aus einem Hoch raus, das spielt doch gar keine Rolle, oder? mn 19. Feb. 2006
Ich bin auch der Meinung, das zumindest eine Bewegung die vom Äquator in Richtung Nordpol führt scheinbar nach links und NICHT nach rechts abgelenkt wird. Vielleicht sollte man bei dem Bild für die Luftmassen einen entsprechenden Kommentar bringen der nochmal deutlich darauf hinweist... bei uns wurde das Bild nämlich in einer VL gebracht - und das verwirrte mich beim Lernen total! 23. Juli 2006
Bewegung entlang des Äquators
Moin,
als Gelegensheitsgleitschirmflieger tauchte bei der Meteorologie folgende Frage auf:
Wirkt die C- Kraft, wenn das Objekt sich auf der Erdobefläche ENTLANG des Äquators (also mit konstantem Radius entlang der Kreibahn in Ost / West Richtung) bewegt?
Meines Erachtens wirkt die C- Kraft / der Effekt bei gegebener Masse, Geschwindigkeit, Winkelgesch. nur durch Veränderung des Radius.
Ich konnte hierzu keine befriedigente Antwort finden und würde mich über eine Antwort/Links auf reom@gmx.de freuen.
Grüße, Robert
- Ich antworte lieber hier: siehe Artikel. Entscheidend ist ob man sich auf die Drehachse zu, oder von ihr weg bewegt. In diesem Fall wirkt sie nicht (man kann auch mal was in die Gleichung einsetzen, die steht da nicht zum Spaß). --Saperaud ☺ 17:08, 12. Jun 2005 (CEST)
Danke, das war mir bekannt. Ich muss dies nur einem Gleitschirmlehrer BELEGEN! Insbesondere, da er nicht von einem idealen Körper ausgeht, sondern mit den durch die C- Kraft bewegten Luftmassen agumentiert. Mein Versuch, ihm die Formel und deren Variablen darzulegen, war nicht erfolgreich:-)
Hierzu benötige ich Quellen o.ä. Ich würde mich über die Unterstützung freuen.
Grüße, Robert
- Die Grafik, eine Drehteller-Spielplatz-Analogie oder das was Herr Lesch dazu sagt sind im Artikel (ein Vergleich mit dem englischen Artikel lohnt auch fast immer). Zum suchen habe ich keine Zeit, ich würde aber bei Google anfangen. Zu belegen hätte dein Lehrer etwas wenn er behauptet es gäbe die Corioliskraft nicht oder sie wäre am Äquator besonders stark. Du musst das höchstens erklären. Oft wird die Corioliskraft dabei mit der Zentrifugalkraft verwechselt, was man auch ausschließen muss. Das mit den Luftmassen verstehe ich nicht. Es ist doch das wichtigste Anwendungsfeld der Corioliskraft, was gibt es da zu argumentieren bzw. gegen oder für was argumentiert er da? Was meinst mit einem idealen Körper? Bei Winden empfehle ich noch die Artikel Gradientkraft und Geostrophischer Wind zu lesen bzw. sich zu diesen zu informieren. --Saperaud ☺ 21:58, 13. Jun 2005 (CEST)
Mit einer Suche bei Google hatte ich angefangen :-) Die Diskussion hing sich bei der Aussage auf, dass die C - Kraft auch auf einen Körper wirkt, der sich entlang des Ä. bewegt (und eine Ablenkung in N oder S- Richtung bewirkt?! Die wollte ich entkräften. Bei diesen "Stammtisch"-Diskussionen benötigt man aber "Beweise" :-) Meine Ausführungen zu der Formel und der Abhängigkeit der C - Kraft vom Radius wurde nicht akzeptiert :-( Also suche ich die explizite Aussage, dass die C - Kraft auf einen Körper, der sich entlang des Ä. bewegt NICHT wirkt.
M.W. ist ein ideale Körper ein Massepunkt ohne räumliche Ausdehung.
Grüße, Robert
- Ich dachte erst an ein Abfragegespräch nach dem Motto "der Lehrer stellt sich dumm". Erstens die Corioliskraft wirkt nicht, diesen Sprachgebrauch dringend vermeiden. Es gibt da keine Wirkung bzw. Wechselwirkung, sondern nur einen Effekt der eben bestimmte Ursachen hat. Die Corioliskraft=besser Coriolis-Effekt ist keine Kraft die einem vom Weg abringt, sondern ein Effekt innerhalb eines rotierenden Systems der dies macht und lediglich wie eine Kraft erscheint. Gehe auf den nächsten Spielplatz, setze dich in so ein Drehdingens, und dann laufe während sich das Ding dreht einmal im konstanten Abstand zur Drehachse (also in Kreisbahn) und einmal auf diese zu. Die Fliehkraft weggedacht ergibt die Corioliskraft. Der Effekt: wenn du dir die Stelle makierst von der du losgehst und ebenfalls die Stelle zu der du in gerader Linie hinwillst, so wird der Weg den du am Ende nimmst eben nicht gerade sein, sondern gebogen. Mit abstrakteren Begründungen scheint man da eh nichts ausrichten zu können. --Saperaud ☺ 16:47, 14. Jun 2005 (CEST)
- PS: Was mir gerade noch einfällt. Frage ihn mal weshalb bei es am Äquator zyklostrophische Winde (Gleichgewicht zwischen Durckgradient- und Zentrifugalkraft) gibt. Diese basieren darauf das die Corioliskraft dort schwach ist. Eigentlich basiert die ganze atmosphärische Zirkulation zu einem guten Teil hierauf, ergo was unterrichtet dieser Mensch nochmal? --Saperaud ☺ 16:52, 14. Jun 2005 (CEST)
Hm, mal ganz naiv gefragt: In welche Richtung soll diese Kraft denn zeigen?
- nach Norden oder Süden: geht aus Symmetriegründen nicht
- nach Westen oder Osten: geht wegen Energieerhaltung nicht
- nach oben oder unten: nennt sich Zentrifugalkraft, nicht Corioliskraft
--Gunther 17:01, 14. Jun 2005 (CEST)
- Ich habe mir mal erlaubt, die Zwischenüberschrift wieder rauszuwerfen, das war nämlich als elementares Argument für die oben aufgeworfene Frage gedacht. (Von daher passt Deine Antwort auch nicht.)--Gunther 17:26, 14. Jun 2005 (CEST)
Hallo,
das hier eine Scheinkraft vorliegt und nicht die Wirkung einer Kraft ist unstrittig. Bitte entschuldigt die unklaren Ausdrucksweise.
Das Beispiel mit dem Kinderspielplatz ist gut, ergibt aber keine eindeutige Klärung.
Das der C - Effekt am Ä. schwach ist, wird der kleineren Radiusänderung und somit kleineren Änderung des Abstandes bei einer Bewegung in Richtung Norden (Süden) hin zur Erdachse zugeschieben.
Die (m.E. falsche) Aussage lautet: Bei einem Körper, der sich entlang des Ä. in Richtung Osten (Westen) bewegt, tritt der C - Effekt in Richtung Süden ( Norden) auf.
Diese möcht ich gern anschaulich einem Nichtmathematiker widerlegen.
Grüße, Robert
- Siehe oben: Die Situation ist spiegelsymmetrisch an der Äquatorebene, deshalb muss auch die Kraft symmetrisch sein. Aber diese Spiegelung vertauscht gerade Norden und Süden, also kann die Kraft weder nach Norden noch nach Süden zeigen. Ist das zu mathematisch?--Gunther 18:25, 14. Jun 2005 (CEST)
Hallo Gunther,
ja, leider:-( Meine letzte Mathestunde.....
Ich würde gern eine genauere Erklärung erhalten, warum die Spiegelsymmetrie eine Kraft in Richtung N odr S ausschließt.
Die in dem Artikle genannte Formel bedingt m.E. ein Geschindigkeit des Körpers in Richtung (oder weg von) der Drehachse. Bewegt sich der Körper aber auf der Kreisbahn ist diese = Null, d.h. F(c) = Null und somit tritt der C - Effekt nicht auf.
Wie erkläre ich aber einem Hobbymeteorologen, das dies mathematische Lösung auch in der (komplexen) Natur so eintritt.
Grüße, Robert
- Hm, es gibt gewissermaßen keinen wesentlichen Unterschied zwischen Nord und Süd in dieser Situation. Mit derselben Berechtigung, mit der eine Kraft nach Norden auftritt, müsste auch eine Kraft nach Süden auftreten. Anders gesagt: Wenn Du auf dem Äquator entlangfährst, dann ist rechts und links von Dir genau dasselbe, nämlich jeweils eine halbe Erdkugel. Aber die Natur kann nicht zwischen links und rechts unterscheiden (in der modernen Physik ist dieser Satz nicht korrekt, aber das spielt hier keine Rolle).--Gunther 19:35, 14. Jun 2005 (CEST)
- Tja ehrlich gesagt läuft das auf die Gegenfrage hinaus: was spricht dafür/wie kann man beweisen das es anders ist? Also entweder Mathematik, ein gutes Vorstellungs- und Abstraktionsvermögen vom Spielplatz auf den Äquator oder eben Messungen machen. Im englischen Artikel steht auch noch ne Menge. --Saperaud ☺ 19:41, 14. Jun 2005 (CEST)
Ha, jetzt habe ich verstanden, warum am Ä. aufgrund der Symmetrie kein C - Effekt in N oder S - Richtung auftreten kann: Die Spiegelsymmetrie schßließt das aus.
Nun kann ich das aber immernoch nicht einem Hobbymeteorologen erklären:-( Trotzdem Danke fü die Antworten, Robert
Eine kleine Anmerkung zur Corioliskraft am Äquator bei Bewegung von Ost nach West: Weil die C.Kraft durch ein Kreuzprodukt aus dem Winkelgeschwindigkeitsvektor und dem Geschwindigkeitsvektor beschrieben wird, steht sie auf diesen beiden Vektoren stets senkrecht. Für eine Ost - West Bewegung am Äquator bedeutet dies, dass die Corioliskraft bei Berücksichtigung der Vorzeichen genau zum Erdmittelpunkt hin zeigt. Daher führt sie zu keiner Ablenkung in einer der Himmelsrichtungen. Liebe Grüße, Andreas
Übersetzung
Die Bilder aus dem englischen Artikel sind alle bei den Commons, es müsste also nur noch der Text übersetzt, angepasst und vielleicht etwas erweitert werden. Freiwillige vor. --Saperaud ☺ 18:57, 28. Jul 2005 (CEST)
Fehler in der Abbildung?
Müssten die Pfeile nicht genau anders herum gerichtet sein? Also auf der Nordhalbkugel gegen den Uhrzeigersinn? -- sk 09:50, 18. Okt 2005 (CEST)
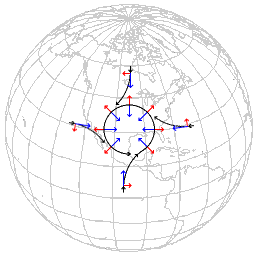
- Das Bild ist schon korrekt. Entscheidend ist die Bemerkung »bei Abwesenheit anderer Kräfte«. Bei Hoch- und Tiefdruckgebieten spielt daneben der Druckgradient eine wichtige Rolle. Das ist auch im Bild drüber dargestellt, aber es hat eine Erläuterung gefehlt, die ich nun ergänzt hab. --.x 15:58, 24. Okt 2005 (CEST)
Hallo, mir ist vollkommen unverständlich aus welchem Grund die C-Kraft bei einer Bewegung nicht nur entlang des Äquators, sondern überhaut in jeder anderen Breite (von Ost nach Süd, oder umkehrt), also parallel zum Äquator auftreten sollte, wie hier aus der Zeichnung hervorgeht ??!! Ich dachte die C-Kraft tritt nur bei Bewegungen zu, oder von den Polen auf. Kann mir das bitte jemand erklären ? Ilja
- Schreib um welche Textpassage es dir geht und widerspreche dir bitte nicht selbst. --Saperaud ☺ 08:50, 7. Nov 2005 (CET)
Mir geht es genau wie Ilja. Wenn ich im Folgenden einen Denkfehler machen sollte, so bitte ich darum, ihn begründet zu korrigieren. Anhand der Abbildung mit dem einzelnen Luftwirbel möchte ich meine Gedanken darlegen:
Es sind dort vier Winde dargestellt, die alle in das sich drehende System einfließen. Der erste strömt von Norden her und würde sich auch geradlinig weiter nach Süden bewegen, wenn er nicht von der Corioliskraft abgelenkt werden würde, die ihn eine Wendung nach rechts vollziehen lässt (der Pfeil deht nach links). Bis hierher stimme ich mit der Darstellung volkommen überein. Die Corioliskraft kommt durch die Drehung der Erde zustande, denn die Luft, die von Norden nach Süden strömt, kann der Drehung der Erde aufgrund ihrer eigenen "Bewegungsträgheit" nicht folgen, sodass es von der Erde aus gesehen so scheint, als ob die Luft nach rechts abdrehen würde. Die Ablenkung erfolgt also auf der Abbildung entgegen der Drehrichtung der Erde! Doch nun der zu Luft, die aus Westen und aus Osten kommt:
Sie weht parallel zum Äquator und "parallel" zur Drehrichtung der Erde. Wieso sollte sie ebenfalls von der Coriolis Kraft nach rechts abgelenkt werden?? Hier hört meine Vorstellungskraft auf. Sie weht doch nicht quer zur Erddrehung, müsste also auch von der Erde aus gesehen geradeaus wehen.
Nun der Wind aus Süden: Auch er müsste doch scheinbar entgegen der Drehrichtung der Erde abgelenkt werden, also nach LINKS.Dies hat sich mir bestätigt, als ich mit Kreide einen geraden Strich, der einen Wind darstellen sollte, von Süden nach Norden auf einen Globus zeichnete, den ich währenddessen drehte. Der Strich änderte keineswegs seine Ablenkungsrichtung, nachdem er den Äquator überquert hatte.Auf der Abbildung dreht sich der Wind allerdings nach rechts. Warum aber um alles in der Welt? Warum erhält jede Bewegung eine Ablenkung nach RECHTS?, auch die parallel zum Äquator? Über Aufklärung wäre ich sehr froh! Danke. Jonathan, 19.11.05
- Schau dir mal eine Karte mit dem Äquator an und vergleiche das mit den rechts abgebildeten Kontinenten. Das ganze Schema spielt sich auf der Nordhalbkugel ab, ungefähr beim nördlichen Wendekreis. --Saperaud ☺ 15:14, 24. Nov 2005 (CET)
Drehung der Nabelschnur
Die Nabelschnur ist in sich verdreht, im Allgemeinen nach links (von der Mutter bzw. der Plazenta aus gesehen) mit einer durchschnittlichen Anzahl von 2,1 Umdrehungen pro 10 cm. Es ist unklar, ob diese Nabelschnurdrehung bei Schwangerschaften der südlichen Hemisphäre umgekehrt verläuft, d.h. ob die Corioliskraft auch hier eine Rolle spielt (siehe hier). Weiss jemand näheres? -- Peter Sinn 13:09, 18. Dez 2005 (CET)
Nicht alles, was gedreht ist, liegt an der Corioliskraft. Oder sind Korkenzieher im Süden andersrum? Oder gar die Doppelhelix im Erbgut? Sind Flugzeuge genagelt, weil sich Schrauben beim Überqueren des Äquators rausdrehen würden? ;-)*kopfschüttel* DerSchim 10:42, 19. Dez 2005 (CET)
Soll das witzig sein? Das ist Proletengeschwafel auf Trinkhallenniveau. Der Fetus ist freischwebend in der Fruchthöhle aufgehängt, also warum soll die Corioliskraft nicht wirken? -- 23:53, 19. Dez 2005 (CET)Das sind absolute Spekulationen ins Blaue, noch ohne Beleg (d. h. absoluter Quatsch). Bei den vielen Störungen spielt eine Kraft wie die Corioliskraft überhaupt gar keine Rolle. Sowas ist absolut sinnfrei und lohnt keiner weiteren Erörterung. Hab mal alles durchgestrichen, hat's nicht anders verdient --Hubi 07:44, 20. Dez 2005 (CET)
Einfachere Erklärung, wie der Coriolis-Effekt entsteht
Die derzeitige Erklärung, wie der Coriolis-Effekt in der Atmosphäre entsteht und sich auswirkt, möchte ich gerne ändern. Ich schlage vor, den zweiten Absatz unter dem Titel Corioliskraft in der Atmosphäre durch die folgende, in meinen Augen einfachere und anschaulichere Erklärung zu ersetzen, und ihn dann an als ersten Absatz zu nehmen. Die Quelle ist [2], den ersten Absatz habe ich etwas abgeändert.
Wie schon erwähnt, entsteht der Coriolis-Effekt durch die Rotation der Erde. Je näher man gegen den Äquator kommt, desto schneller bewegt sich ein Punkt an der Oberfläche. Wenn nun ein Luftpaket seine geografische Breite verlässt, behält es seine Geschwindigkeit bei. Wenn es also beispielsweise vom Äquator nach Norden strömt, kommt es in Breiten, die sich langsamer bewegen als seine Herkunftsregion. Das Luftpaket bewegt sich hier dann schneller als die Erde unter ihm, es wird also scheinbar nach Osten abgelenkt. Strömt aber ein Paket auf der Nordhalbkugel von Norden nach Süden, dann gelangt es in „schnellere“ Breiten. Jetzt dreht sich der Boden schneller als das Luftpaket, und geschieht eine Ablenkung nach Westen. Auf der Südhalbkugel ist es aber anders herum.
Die Coriolis-Kraft lenkt also Strömungen:
- auf der Nordhalbkugel nach rechts und
- auf der Südhalbkugel nach links ab.
Grafik [3] würde hier eingefügt.
Sie wirkt aber nur bei grossräumigen Strömungen, wo sehr grosse Massen im Spiel sind. Bei den regionalen Windsystemen ist sie beispielsweise zu vernachlässigen.
Die Corioliskraft bewirkt auch die zyklonale Drehung von Tiefdruckgebieten und die antizyklonale Drehung von Hochdruckgebieten. Tiefdruckgebiete drehen sich auf der Nordhalbkugel linksherum, weil die Coriolis-Kraft bewegende Luft nach rechts ablenkt. Dieses Paradoxon erklärt die folgende Grafik.
Grafik [4] würde hier eingefügt.
Die Luft müsste eigentlich entlang des Druckgradienten direkt in das Tiefdruckgebiet strömen. Da sie aber auf der Nordhalbkugel durch die Coriolis-Kraft nach rechts abgelenkt wird, strömt sie am Tief „vorbei“ (1). An allen Stellen um das Tief herum (2 und 3) wirkt der Druckgradient direkt zum Zentrum der Zyklone. Da aber auch hier die Luftströmung durch die Coriolis-Kraft abgelenkt wird, erreicht sie nicht das Tief. Somit bewegt sich die Luft um das Tief also insgesamt (4) gegen den Uhrzeigersinn (Linksdrehung).
Die aus Hochdruckgebieten ausströmende Luft wird auf der Nordhalbkugel nach rechts abgelenkt. Sie drehen sich also rechts herum (im Uhrzeigersinn).
Da auf der Südhalbkugel Strömungen durch die Coriolis-Kraft nach links abgelenkt werden, gelten die soeben beschriebenen Vorgänge anders herum: Tiefdruckgebiete drehen sich auf der Südhalbkugel im Uhrzeigersinn, Hochdruckgebiete gegen den Uhrzeigersinn.
- Dies ist eine (leider häufige) falsche Erklärung der Corioliskraft! Der von dir beschriebene Effekt wäre durch die Massenträgheit verursacht. Die Ursache der Corioliskraft ist aber die Erhaltung des Drehimpuls. Ausserdem ist in deiner Erklärung die Reibung im Spiel. In der Animation mit der sich bewegenden Kugel bewegt sich der Körper ohne Reibung nach aussen. Ausserdem würde bei dieser Erklärung der nach Norden fahrende Zug nicht nach Osten gedrückt werden, da er ja immer mit der Erde verbunden ist.
- Die Corioliskraft lässt sich einfacher verstehen, wenn man sich eine Pirouette vorstellt. Jeder weiss, wenn die Eiskunstläuferin ihre Arme nach aussen nimmt, wird sie langsamer. Der Drehimpuls muss konstant bleiben. Bei der Scheibe mit der konstanten Drehgeschwindigkeit, bzw. der sich (mehr oder weniger) konstant drehenden Erde muss die Masse die nach aussen bewegt deshalb langsamer werden. Innerhalb des Bezugsystems wird sie abgelenkt. Wernfried 16:51, 25. Mär 2006 (CET)
Auf die Frage, WAS die Corioliskraft IST; (ohne auf die Effekte, Wirkungen etc eingehen zu wollen) mal noch ein Versuch, das verständlich zu machen: Ein Körper rotiert mit konstanter Geschwindigkeit (nämlich genau sooo schnell, wie das Bezugssystem, in diesem Fall die Erde sich dreht) auf der Äquatorlaufbahn. Wird dieser Körper nun (warum auch immer) nach Norden oder Süden (genau in Richtung des Pols) beschleunigt/ bewegt, so verringert sich der Radius seiner Laufbahn bei gleichbleibender Bewegungsenergie (gleichem Impuls?) und er wird schneller. (Pirouetteneffekt). Umgekehrt (wie beim Kugelbeispiel:) Ein Körper wird aus der Nähe eines Pols zum Äquator beschleunigt. Da der Radius größer wird, verringert sich die Drehgeschwindigkeit, sodass die Erddrehung immer schneller wird in Bezug auf die Rotation des Körpers. Und jetzt der Punkt: Ein außenstehender Beobachter betrachtet das rotierende Bezugssystem (die sich drehende Erde) mit dem bewegten Körper darauf, sieht den Körper sich in der gekrümmten Bahn bewegen, sieht den sich verändernden Radius usw und denkt sich nichts dabei. Für einen sich auf dem Bezugssystem befindenden Beobachter scheint es aber, als würde sich der Körper wie von Geisterhand von ihm weg bzw. auf ihn zu bewegen (jenachdem, ob der Körper vom Pol oder vom Äquator kommt). Für eine solche Bewegung bedarf es aber aus Sicht eines solchen Beobachters einer den Körper beschleunigenden Kraft, die de fakto nicht vorhanden ist. Daher ist die Cor.- Kraft eine Scheinkraft. ...Stimmt das?
- Eigentlich muss die absolute Geschwindigkeit der Bewegung (und nicht nur die Winkelgeschwindigkeit) steigen, weil die Tagngentialkomponente der Geschwindigkeit erhalten bleibt (der Körper will sich eigentlich mit konstanter Geschwindigkeit gerade weiterbewegen, wird aber von einer Kraft dazu gezwungen, sich auf der Oberfläche der Kugel zu bewegen). -MrBurns 16:19, 14. Feb. 2007 (CET)
Wasserstrudel in der Badewanne
Hallo, zum Thema Bedewannenstrudel gibt es einen sehr interessanten Artikel hier: http://www.wissenschaft-online.de/abo/spektrum/archiv/5296 Der klärt auf über die etwas widersprüchlichen Aussagen zur Frage, ob die Corioliskraft jetzt Verursacher der Strudel ist oder nicht auf. Kurz gesagt: Sie ist Verursacher, aber nicht direkt. Sie verursacht eine Ablenkung der Wasserteilchen auf dem Weg zum Ablauf hin, wodurch sich im Ablauf selbst eine Drehbewegung bildet, die aufgrund der Drehimpulserhaltung deutlich schneller ist, als erwartet. Ich finde, die beiden Erklärungen auf dieser Seite und auf der Seite Strudel (Physik) erklären dies nicht eindeutig und widersprechen sich zudem ein bißchen. Bevor ich da was ändere, hätte ich gerne noch eine zweite Meinung. Gruß, -- Flatlander3004 09:11, 28. Apr 2006 (CEST)
Da stimme ich dir zu, im Artikel sieht es so aus als waere es Zufall oder Geisterhand die den Strudel in entsprechende richtung strudeln laesst. -- Delete
- Man kann es sich auch so vorstellen: in einer Badewanne ist das Wasser im nördlichen Badewannenbereich der Drehachse der Erde näher als das Wasser im südlichen Bereich der Badewanne (gilt auf der Nordhalbkugel). Erfährt jetzt Wasser, das zunächst in Ruhe (!) ist, eine Bewegung in Nord-Süd-Richtung (und dies ist spätestens beim Öffnen des Abflusses der Fall), wird der Coriolis-Effekt sichtbar (von Coriolis-Kraft sollte man m.E. gar nicht reden).
- Das heißt, auf der sich nach Osten drehenden Erde werden nach Süden, und damit auch nach 'außen' (d.h. von der Erddrehachse weg, Richtung Weltraum) wandernde Wasserteilchen langsamer als die Erddrehung (wie z.B. auch beim Ausstrecken der Arme eines Eisläufers bei einer Pirouette diese langsamer werden), d.h. es ist eine Ablenkung des Wassers nach Westen zu beobachten.
- Die nach Norden (und damit auch in Richtung der Erddrehachse) wandernden Wasserteilchen werden schneller als die Erddrehung (entspricht dem Effekt beim Anziehen der Arme eines Eisläufers bei einer Pirouette), also nach Osten abgelenkt, so dass sich die Bewegung des Wassers gegen den Uhrzeigersinn (um den Abfluss herum) bildet.
- Ist dieser Mechanismus erst einmal in Gang gesetzt, gilt, wie es oben korrekt heißt: im Ablauf selbst bildet sich eine Drehbewegung, die aufgrund der Drehimpulserhaltung recht schnell wird.
- Gruß, Hpt 19:48, 11. Nov. 2006 (CET)
- Nunja, es gibt wohl kein Wissenschaftsmagazin, dass das noch nicht behandelt hat. :-) Es gab auch mal einen Disput zwischen Armin (von der "Maus" und Christoph Drösser ("Stimmt's" in der ZEIT), wo letzterer den ersteren "erstaunliche Beratungsresistenz" vorgeworfen hat. Allerdings ist es wohl so wie bei Radio Eriwan (wenn ich die Quelle noch wüsste, würde ich sie angeben): "Im Prinzip schon, aber erst wenn der Abfluss einen Durchmesser größer 10 Meter hat". Ähnliches Problem wie bei der Mindestlänge eines Foucaultschen Pendels. <eg>--80.136.155.131 18:50, 15. Feb. 2007 (CET)
Im Artikel steht korrekt, dass die Wasserstrudel in der Regel von allem anderen ((auch winzige) Unebenheiten in der Wanne fehlen noch) abhängt, aber nicht von der Lage nördlich oder südlich des Äquators. Aber ich erinnere mich an einen Fernsehbeitrag vor vielen, vielen Jahren (könnte noch in den 60ern, spätestens 70ern gewesen sein), wo ein englischer (oder australischer) Forscher einen riesigen, runden Wassertank gebaut hat, den er nach allen Regeln der Kunst gleichmäßig und eben ausgeführt hat, und in dessen Mitte ein kleines Abflussloch war. Diesen Tank hat er dann zuerst in England und dann in Australien aufgestellt, und der Strudel drehte sich vollkommen nach Theorie wie die jeweiligen Tiefdruckgebiete. Es wurde aber keine Abschätzung vorgenommen, ob da immer noch bestehende Rauigkeiten oder sonstige Unebenheiten oder Verformungen durch den Transport mehr Einfluss gehabt haben können als die Geografie. --PeterFrankfurt 01:23, 10. Dez. 2007 (CET)
Bildwarnung
Die unten genannten Bilder, die in diesem Artikel verwendet werden, sind auf Commons gelöscht oder zur Löschung vorgeschlagen worden. Bitte entferne die Bilder gegebenenfalls aus dem Artikel oder beteilige dich an der betreffenden Diskussion auf Commons. Diese Nachricht wurde automatisch von CommonsTicker erzeugt.
- Sanbec setzt Lösch-Marker Duplicate für Image:Corioliskraftanimation.gif
- duplicate, the other version uploaded much before (diff);
-- DuesenBot 20:19, 16. Sep 2006 (CEST)
Ursache der Corioliskraft
Vielleicht überseh ich da ja etwas, aber warum soll die Corioliskraft durch die Drehimpulserhaltung erzeugt werden? M.E. hat das damit doch garnichts zu tun (auch wenn gewisse Phänomene damit etwas zu tun haben), sie entsteht ja nur dadurch, dass wir das Bezugssystem wechseln. D.h. sie ist in der fortwährenden Drehung des Bezugssystems gegenüber des Inertialsystems begründet. --87.78.134.207 14:51, 1. Dez. 2006 (CET)
