Sinus hyperbolicus und Kosinus hyperbolicus

Eine Gerade durch den Nullpunkt schneidet die Hyperbel $x^{2}-y^{2}=1$ im Punkt $(\cosh \,A,\sinh \,A)$, wobei $A$ für die Fläche zwischen der Geraden, ihrem Spiegelbild bezogen auf die $x$-Achse und der Hyperbel steht. (Siehe auch die animierte Version mit Vergleich zu den Trigonometrischen (zirkulären) Funktionen.) Die Hyperbel wird auch als Einheitshyperbel bezeichnet.

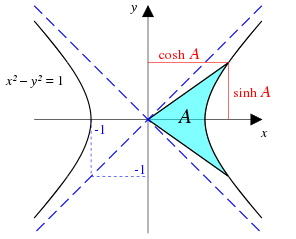
Sinus hyperbolicus und Kosinus hyperbolicus sind mathematische Hyperbelfunktionen, auch Hyperbelsinus bzw. Hyperbelkosinus genannt; sie tragen die Symbole $\sinh$ bzw. $\cosh$, in älteren Quellen auch ${\mathfrak {Sin}}$ und ${\mathfrak {Cos}}.$ Der Kosinus hyperbolicus beschreibt unter anderem den Verlauf eines an zwei Punkten aufgehängten Seils. Sein Graph wird deshalb auch als Katenoide (Kettenlinie) bezeichnet.

Definitionen

• Sinus hyperbolicus

$\sinh x={\frac {1}{2}}\left(e^{x}-e^{-x}\right)=-i\,\sin(i\,x)$

• Kosinus hyperbolicus

$\cosh x={\frac {1}{2}}\left(e^{x}+e^{-x}\right)=\cos(i\,x)$

Die Funktionen sinh und cosh sind also der ungerade bzw. gerade Anteil der Exponentialfunktion ($\exp x=\cosh x+\sinh x$).

Eigenschaften

Sinus hyperbolicus (rot) und Kosinus hyperbolicus (blau) für reelle x.

	Sinus hyperbolicus	Kosinus hyperbolicus
Definitionsbereich	$-\infty <x<+\infty$	$-\infty <x<+\infty$
Wertebereich	$-\infty <f(x)<+\infty$	$1\leq f(x)<+\infty$
Periodizität	keine	keine
Monotonie	streng monoton steigend	$-\infty <x\leq 0$ streng monoton fallend $0\leq x<\infty$ streng monoton steigend
Symmetrien	Punktsymmetrie zum Ursprung	Achsensymmetrie zur Ordinate
Asymptotische Funktionen	$a_{1}(x)={\frac {1}{2}}e^{x},\quad x\to \infty$	$a_{1}(x)={\frac {1}{2}}e^{x},\quad x\to \infty$
	$a_{2}(x)=-{\frac {1}{2}}e^{-x},\quad x\to -\infty$	$a_{2}(x)={\frac {1}{2}}e^{-x},\quad x\to -\infty$
Nullstellen	$x=0$	keine
Sprungstellen	keine	keine
Polstellen	keine	keine
Extrema	keine	Minimum bei $x=0$
Wendestellen	$x=0$	keine

Spezielle Werte

$\sinh(\ln \Phi )={\tfrac {1}{2}}$ mit dem goldenen Schnitt $\Phi$

Uneigentliches Integral

Für den Kosinus hyperbolicus gilt insbesondere:

$\int \limits _{-\infty }^{\infty }{\frac {\mathrm {d} x}{\cosh x}}=\pi .$

Umkehrfunktionen

Der Sinus hyperbolicus bildet $\mathbb {R}$ bijektiv auf $\mathbb {R}$ ab und hat deshalb eine Umkehrfunktion, die man Areasinus hyperbolicus nennt.

Der Kosinus hyperbolicus bildet das Intervall $[0,+\infty [$ bijektiv auf das Intervall $[1,+\infty [$ und lässt sich eingeschränkt auf $[0,+\infty [$ also invertieren. Die Umkehrfunktion davon nennt man Areakosinus hyperbolicus

Beide Umkehrfunktionen, Areasinus hyperbolicus und Areakosinus hyperbolicus, lassen sich folgendermaßen mit Hilfe von elementareren Funktionen berechnen:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \operatorname{arsinh} x = \ln\left(x+\sqrt{x^2+1}\right)\ } .

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \operatorname{arcosh} x = \ln\left(x+\sqrt{x^2-1}\right)\ } .

Ableitungen

Die Ableitung des Sinus hyperbolicus ist der Kosinus hyperbolicus und die Ableitung des Kosinus hyperbolicus ist der Sinus hyperbolicus:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \frac{\mathrm{d}}{\mathrm{d}x} \sinh x & = \cosh x\\ \frac{\mathrm{d}}{\mathrm{d}x} \cosh x & = \sinh x \end{align} }

Stammfunktionen

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \int \sinh x \, \mathrm dx &= \cosh x + C\\ \int \cosh x \, \mathrm dx &= \sinh x + C \end{align} }

Zusammenhänge (zwischen den beiden Funktionen und anderen)

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \cosh^2 x \!\; - \sinh^2 x = 1}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \cosh x \,\; + \sinh x \,\,= e^{x}} (Eulersche Identität)

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \cosh x \,\; - \sinh x \,\,= e^{-x}}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \cosh({\rm arsinh}(x)) = \sqrt{x^2 + 1} }

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sinh({\rm arcosh}(x)) = \sqrt{x^2 - 1} } (Hyperbelgleichung)

Additionstheoreme

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \sinh(x\pm y) &= \sinh x \cosh y \pm \cosh x \sinh y\\ \cosh(x\pm y) &= \cosh x \cosh y \pm \sinh x \sinh y \end{align} }

insbesondere gilt für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y := x} :

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \sinh 2x &= 2\cdot\sinh x \cosh x\ \\ \cosh 2x &= \cosh^2 x + \sinh^2 x = 2\cdot \cosh^2 x - 1 = 2\cdot \sinh^2 x + 1 \end{align} }

und für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle y := 2x} :

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \sinh 3x &= 4\cdot \sinh^3 x +3 \sinh x\ \\ \cosh 3x &= 4\cdot \cosh^3 x -3 \cosh x \end{align} }

Summenformeln

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \sinh x \pm \sinh y & = 2 \sinh \frac{x\pm y}2 \cosh\frac{x\mp y}2 \\ \cosh x + \cosh y & = 2 \cosh \frac{x + y}2 \cosh\frac{x-y}2 \\ \cosh x - \cosh y & = 2 \sinh \frac{x + y}2 \sinh\frac{x-y}2 \end{align} }

Potenzen

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \sinh^2 x = \frac{1}{2} \Big(\cosh (2x) - 1 \Big) \\ \cosh^2 x = \frac{1}{2} \Big(\cosh (2x) + 1 \Big) \end{align} }

Reihenentwicklungen

Die Taylorreihe des Sinus hyperbolicus bzw. Kosinus hyperbolicus mit dem Entwicklungspunkt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x=0} lautet:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \sinh x &= \sum_{n=0}^\infty \frac{x^{2n+1}}{(2n+1)!} = x+ \frac{x^3}{3!} + \frac {x^5}{5!} + \dotsb\\ \cosh x &= \sum_{n=0}^\infty \frac{x^{2n}} {(2n)!} = 1 + \frac{x^2}{2!} + \frac{x^4}{4!} + \dotsb \end{align} }

Produktentwicklungen

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} &\sinh x = x\cdot \prod_{k=1}^\infty \left(1+\frac{x^2}{(k\pi)^2}\right) \\ &\cosh x = \prod_{k=1}^\infty \left( 1 + \frac{4 x^2} {(2k - 1)^2 \pi^2} \right) \end{align} }

Multiplikationsformeln

Sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n\in\N} . Dann gilt für alle komplexen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle z} :

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} &\sinh z = {\left(\frac{2}{i}\right)}^{\!\!n-1} \, \prod\limits_{k=0}^{n-1} \sinh{\frac{z+k\,\pi\,i}{n}}\\ &\cosh z = 2^{n-1} \prod\limits_{k=0}^{n-1} \cosh{\frac{z+\left(k-\frac{n-1}{2}\right)\,\pi\,i}{n}} \end{align} }

Komplexe Argumente

Mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x,y \in \mathbb{R}} gilt:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \sinh(x+i\,y) &= \cos y \, \sinh x + i \sin y \, \cosh x\\ \cosh(x+i\,y) &= \cos y \, \cosh x + i \sin y \, \sinh x\\ \sin(x+i\,y) &= \sin x \, \cosh y + i \cos x \, \sinh y\\ \cos(x+i\,y) &= \cos x \, \cosh y - i \sin x \, \sinh y\\ \end{align} }

So folgen beispielsweise die dritte und die vierte Gleichung auf folgende Weise:

Mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle z = x+i\,y} gilt

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \exp(iz) &= \cos(x+i\,y) + i \sin(x+i\,y)\\ &= \exp(i \, (x+i\,y))\\ &= \exp(i \, x) \, \exp(i \, (i\,y))\\ &=(\cos x \, \cos(i\,y)- \sin x \, \sin(i\,y))+i \, ( \cos x \, \sin(i\,y) + \sin x \, \cos(i\,y) )\\ &=(\cos x \, \cosh y - i \sin x \, \sinh y)+i \, ( \sin x \, \cosh y + i \cos x \, \sinh y )\\ \end{align} }

Durch Koeffizientenvergleich folgt:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \cos(x+i\,y) &= \cos x \, \cosh y - i \sin x \, \sinh y \\ \sin(x+i\,y) &= \sin x \, \cosh y + i \cos x \, \sinh y \\ \end{align} }

Anwendungen

Lösung einer Differentialgleichung

Die Funktion

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f(x)=a \cdot \sinh x+b \cdot \cosh x} mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a,b \in \mathbb{R}}

löst die Differentialgleichung

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f''(x) - f(x) = 0\ } .

Kettenlinie

Ein homogenes Seil, das nur aufgrund seiner Eigenlast durchhängt, kann durch eine Kosinus-hyperbolicus-Funktion beschrieben werden. Eine derartige Kurve nennt man auch Kettenlinie, Kettenkurve oder Katenoide.

Lorentz-Transformation

Mit Hilfe der Rapidität Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda} kann man die Transformationsmatrix für eine spezielle Lorentztransformation (auch Lorentz-Boost) in x-Richtung folgendermaßen darstellen (für Transformationen in andere Richtungen ergeben sich ähnliche Matrizen):

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle L = \begin{pmatrix} \cosh \lambda & -\sinh \lambda & 0 & 0\\ -\sinh \lambda & \cosh \lambda & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix} }

Man sieht eine große Ähnlichkeit zu Drehmatrizen; man erkennt so also gut die Analogie zwischen speziellen Lorentztransformationen in der vierdimensionalen Raumzeit und Drehungen im dreidimensionalen Raum.

Kosmologie

Der Sinus hyperbolicus tritt auch in der Kosmologie auf. Die zeitliche Entwicklung des Skalenfaktors in einem flachen Universum, das im Wesentlichen nur Materie und Dunkle Energie enthält (was ein gutes Modell für unser tatsächliches Universum ist), wird beschrieben durch

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a(t) = \left(\sqrt{\frac{1-\Omega_{\Lambda,0}}{\Omega_{\Lambda,0}}} \sinh\left(\frac{t}{t_\mathrm{ch}}\right)\right)^{2/3}} ,

wobei

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t_\mathrm{ch} = \frac{2}{3 \sqrt{\Omega_{\Lambda,0}} H_0}}

eine charakteristische Zeitskala ist. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle H_0} ist dabei der heutige Wert des Hubble-Parameters, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Omega_{\Lambda,0}} der Dichteparameter für die Dunkle Energie. Die Herleitung dieses Ergebnisses findet man bei den Friedmann-Gleichungen. Bei der Zeitabhängigkeit des Dichteparameters der Materie tritt dagegen der Kosinus hyperbolicus auf:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Omega_M(t) = \cosh^{-2}\left(\frac{t}{t_\mathrm{ch}}\right) } .

Siehe auch

• Areasinus hyperbolicus und Areakosinus hyperbolicus
• Trigonometrische Funktionen
• Kreis- und Hyperbelfunktionen.

Weblinks

• Eric W. Weisstein: Hyperbolic Sine und Hyperbolic Cosine auf MathWorld (engl.)

Einzelnachweise

Trigonometrische Funktion

Primäre trigonometrische Funktionen
Sinus und Kosinus | Tangens und Kotangens | Sekans und Kosekans 

Umkehrfunktionen (Arkusfunktionen)
Arkussinus und Arkuskosinus | Arkustangens und Arkuskotangens | Arkussekans und Arkuskosekans 

Hyperbelfunktionen
Sinus hyperbolicus und Kosinus hyperbolicus | Tangens hyperbolicus und Kotangens hyperbolicus | Sekans hyperbolicus und Kosekans hyperbolicus 

Areafunktionen
Areasinus hyperbolicus und Areakosinus hyperbolicus | Areatangens hyperbolicus und Areakotangens hyperbolicus | Areasekans hyperbolicus und Areakosekans hyperbolicus