Datei:Kerr-surfaces.png
aus Wikipedia, der freien Enzyklopädie
Kerr-surfaces.png (800 × 588 Pixel, Dateigröße: 60 KB, MIME-Typ: image/png)
![]()
Diese Datei und die Informationen unter dem roten Trennstrich werden aus dem zentralen Medienarchiv Wikimedia Commons eingebunden.
Inhaltsverzeichnis
Beschreibung
| BeschreibungKerr-surfaces.png |
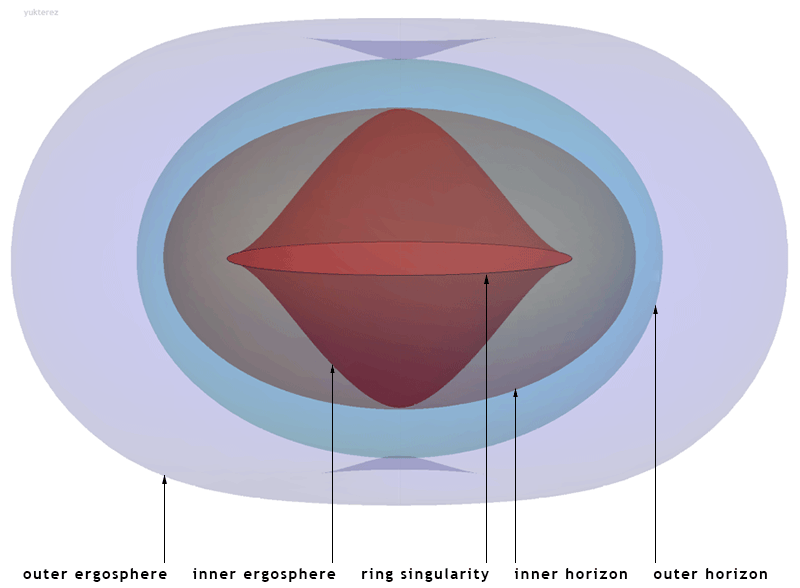
English: Event horizons and ergospheres of a rotating black hole (spin parameter a=Jc/G/M²=0.99); the ring-singularity is located at the equatorial kink of the inner ergosphere at R=a.
Deutsch: Ereignishorizonte und Ergosphären eines mit dem Spinparameter a=Jc/G/M²=0.99 rotierenden schwarzen Lochs. Die Ringsingularität liegt an der äquatorialen Ausbuchtung der inneren Ergosphäre bei R=a. |
| Datum | |
| Quelle | Eigenes Werk (source) |
| Urheber | Yukterez (Simon Tyran, Vienna) |
| Andere Versionen |
  |

|
Dieses Bild des Typs Png sollte als Vektorgrafik im SVG-Format neu erstellt werden. Vektorformate haben zahlreiche Vorteile; weitere Information unter Commons:Media for cleanup. Wenn dir eine SVG-Version dieses Bildes vorliegt, so lade diese bitte hoch. Nach dem Hochladen der Datei ist diese Vorlage auf der aktuellen Bildbeschreibungsseite durch die Vorlage {{Vector version available}}, oder kürzer {{Vva}}, zu ersetzen. Es ist empfohlen die neue SVG-Datei „Kerr-surfaces.svg“ zu nennen – dann benötigt die Vorlage vector version available (bzw. vva) keinen Parameter.
|
Code
rE=1+Sqrt[1-a^2 Cos[θ]^2]; RE[A_]:={Sqrt[rE^2+A^2] Sin[θ]Cos[φ],Sqrt[rE^2+A^2] Sin[θ]Sin[φ],rE Cos[θ]}; (* outer ergosphere *)
rG=1-Sqrt[1-a^2 Cos[θ]^2]; RG[A_]:={Sqrt[rG^2+A^2] Sin[θ]Cos[φ],Sqrt[rG^2+A^2] Sin[θ]Sin[φ],rG Cos[θ]}; (* inner ergosphere *)
rA=1+Sqrt[1-a^2]; RA[A_]:={Sqrt[rA^2+A^2] Sin[θ]Cos[φ],Sqrt[rA^2+A^2] Sin[θ]Sin[φ],rA Cos[θ]}; (* outer horizon *)
rI=1-Sqrt[1-a^2]; RI[A_]:={Sqrt[rI^2+A^2] Sin[θ]Cos[φ],Sqrt[rI^2+A^2] Sin[θ]Sin[φ],rI Cos[θ]}; (* inner horizon *)
p[f_, c_]:=ParametricPlot3D[f, {φ, 0, 2 π}, {θ, 0, π}, PlotStyle -> Directive[c, Opacity[0.15]]] (* plotfunction *)
Do[Print[Show[p[RE[a], Blue], p[RA[a], Cyan], p[RI[a], Orange], p[RG[a], Red]], {a,0,1,0.1}]] (* cartesian, x,y,z *)
Do[Print[Show[p[RE[0], Blue], p[RA[0], Cyan], p[RI[0], Orange], p[RG[0], Red]], {a,0,1,0.1}]] (* pseudospherical, r,θ,Ф *)
Comparison
- Boyer-Lindquist: doi:10.1139/p81-086 Nigel Sharp: On embeddings of the Kerr geometry; page 3, figure 3
- Kerr-Schild: Matt Visser: The Kerr spacetime, A brief introduction; page 35, figure 3
- Source: kerr.yukterez.net / kerr.newman.yukterez.net
Lizenz
Ich, der Urheber dieses Werkes, veröffentliche es unter der folgenden Lizenz:
Diese Datei ist lizenziert unter der Creative-Commons-Lizenz „Namensnennung – Weitergabe unter gleichen Bedingungen 4.0 international“.
- Dieses Werk darf von dir
- verbreitet werden – vervielfältigt, verbreitet und öffentlich zugänglich gemacht werden
- neu zusammengestellt werden – abgewandelt und bearbeitet werden
- Zu den folgenden Bedingungen:
- Namensnennung – Du musst angemessene Urheber- und Rechteangaben machen, einen Link zur Lizenz beifügen und angeben, ob Änderungen vorgenommen wurden. Diese Angaben dürfen in jeder angemessenen Art und Weise gemacht werden, allerdings nicht so, dass der Eindruck entsteht, der Lizenzgeber unterstütze gerade dich oder deine Nutzung besonders.
- Weitergabe unter gleichen Bedingungen – Wenn du das Material wiedermischst, transformierst oder darauf aufbaust, musst du deine Beiträge unter der gleichen oder einer kompatiblen Lizenz wie das Original verbreiten.
Kurzbeschreibungen
Horizonte und Ergosphären eines rotierenden schwarzen Lochs
Horizon- and ergosurfaces of a rotating black hole
In dieser Datei abgebildete Objekte
Motiv
Einige Werte ohne einen Wikidata-Eintrag
25. Juni 2017
61.227 Byte
588 Pixel
800 Pixel
image/png
df5780df94d1245cf657e8a89dec646c7abc5bbe
Dateiversionen
Klicke auf einen Zeitpunkt, um diese Version zu laden.
| Version vom | Vorschaubild | Maße | Benutzer | Kommentar | |
|---|---|---|---|---|---|
| aktuell | 02:48, 29. Aug. 2021 |  | 800 × 588 (60 KB) | wikimediacommons>Yukterez | pointing the arrows to the outer edges of the surfaces to avoid 2D/3D confusions |
Dateiverwendung
Die folgende Seite verwendet diese Datei:
Metadaten
Diese Datei enthält weitere Informationen (beispielsweise Exif-Metadaten), die in der Regel von der Digitalkamera oder dem verwendeten Scanner stammen. Durch nachträgliche Bearbeitung der Originaldatei können einige Details verändert worden sein.
| Software |
|
|---|
Abgerufen von „https://de.wikiup.org/wiki/Datei:Kerr-surfaces.png“