Diskussion:Lagrange-Punkte/Archiv/1
Weblinks
- http://www.wappswelt.de/tnp/nineplanets/help.html => Lagrange
- http://www.winkler-berlin.de/Deutsch/Dorbit.htm
Versionsgeschichte von Punkt L1
* (Aktuell) (Letzte) . . 17:35, 21. Mai 2004 . . Terabyte * (Aktuell) (Letzte) . . 11:05, 19. Mai 2004 . . Terabyte * (Aktuell) (Letzte) . . 11:04, 26. Nov 2003 . . Geof * (Aktuell) (Letzte) . . 10:54, 26. Nov 2003 . . Geof
- Wenn ich das richtig sehe, stand das alles schon drin. Hat sich damit wohl erübrigt. --Wolfgangbeyer 21:33, 21. Mai 2004 (CEST)
- Der zweite Link www.winkler-berlin.de ist tot. Ist die Seite umgezogen, nur temporär nicht erreichbar oder ganz verschwunden? TTL 14:25, 4. Feb. 2007 (CET)
- Ok, den Link hat inzwischen jemand entfernt. War auch eben weiterhin nicht erreichbar. TTL 14:34, 18. Feb. 2007 (CET)
Hallo anonymer Mitautor,
Ich habe deine Änderungen mit meinen umfrangreichen Änderungen überschrieben, da ich entweder unklare Sätze (wie in der Einleitung) schon selber in der Zwischenzeit verbessert habe oder deine Änderungen nicht ganz korrekt waren (wie der Name des James Webb Space Telescope das früher Next Generation Space Telescope hieß, wie auch dem Wikipediaartikel dazu entnommen werden kann) oder ich nicht so gut fand (wie den Begriff Sonnensatellit, statt Sonnenbeobachtungssatellit.)
Ich bin mir sicher, dass einige meiner umfangreichen Änderungen noch ein wenig Polierarbeit durch andere benötigen. Bitte entschuldige auch eventuelle von mir zu rigoros zurückgenommene Änderungen von dir. Arnomane 00:19, 13. Sep 2004 (CEST)
Ist es wirklich gut, hier einen ganzen Block des Artikels Trojaner eins zu eins übernommen zu haben? Sollte da nicht besser ein Link hinführen? IMHO haben Lagrange-Punkte eine allgemeinere Bedeutung als nur für die Astronomie (das ist dann ja die Anwendung (und der Auslöser der Forschung in der Richtung)). --Nightstalker 17:15, 21. Jun 2005 (CEST)
Erdbegleiter
Im Abschnitt "Erdbegleiter" heisst es: "Es wurden bislang in den L4- und L5-Punkten des Erde-Sonne-Systems in den 1950ern Staubwolken gefunden." Die Kordylewskische Wolken in den L4- und L5-Punkten des Systems Erde-Mond sind mir bekann, aber gibt es tatsächlich Staubwolken in den L4/L5-Punkten des Systems Erde-Sonne? Gibt es Quellen dazu? --Vesta 15:02, 7. Jun 2006 (CEST)
- Ich mutmaße mal, dass die L4 und L5 des Systems Erde-Sonne nicht so stabil sind, da die Erde ja mit dem Mond einen recht großen Begleiter hat, der die Lagrange-Punkte vielleicht zu sehr stören könnte... --RokerHRO 20:48, 28. Jan. 2010 (CET)
Stabilität von L4 und L5
die stabilität bzw. instabilität der lagrangepunkte ist hier sehr schön und detailliert beschrieben... also bitte, liebe IP, lies und rechne dir das erstmal durch, bevor du wieder deine seltsamen theorien postest...--moneo d|b 15:20, 12. Jun. 2007 (CEST)
- Ach – daher kommen all diese merkwürdigen Abbildungen. Die Darstellung ist völlig übertrieben kompliziert und daher praktisch nicht nachvollziehbar. Die Sache ist aber im Grunde ganz einfach. Wie oben dargelegt braucht eigentlich nur die Wechselwirkung der Sonne mit Trojaner und Planet (zwei unabhängige Zweikörperprobleme) berücksichtigt werden, weil in L4/L5 die Anziehung der Sonne mindestens 1000-fach stärker ist. In dieser Näherung ist sofort klar, dass die Lösung nicht derart "stabil" ist, dass der Winkelabstand von Planet und Trojaner gleich bleibt. Der Trojaner läuft bei einer kleinen Abweichung entweder etwas langsamer oder schneller um und wird daher vom Planeten überholt oder holt umgekehrt den Planeten langsam ein. Ein genauere Berechnung ist unsinnig, weil dann konsequenter Weise nicht nur Trojaner und Planet sondern auch die anderen Planeten berücksichtigt werden müssen und zudem sich die Planetenbahnen in Wahrheit keine Kreise (siehe Kepler-Gesetze). 84.59.49.249 22:34, 12. Jun. 2007 (CEST)
- das was du "völlig übertrieben kompliziert" nennst, ist die physikalisch und mathematisch korrekte art, die lagrangepunkte zu beschreiben. du kannst lagrangepunkte nicht in nem zweikörperproblem beschreiben! dazu braucht man das eingeschränkte dreikörperproblem! nur weil das vielleicht zu hoch für dich ist, ist deswegen nicht falsch. (übrigens, auch wenn man die anderen planeten berücksichtigt, gibt es lagrange-punkte... allerdings nicht mehr 5 sondern mehr; und die ganze angelegenheit wird noch etwas komplizierter). deine "näherung" ist eben nur eine "näherung" - und leider eine schlechte... aber du scheinst ja leider resistent gegen argumente zu sein - also zweifle ich, das es nützt, dir hier was erklären zu wollen... --moneo d|b 22:57, 12. Jun. 2007 (CEST)
- Ach – daher kommen all diese merkwürdigen Abbildungen. Die Darstellung ist völlig übertrieben kompliziert und daher praktisch nicht nachvollziehbar. Die Sache ist aber im Grunde ganz einfach. Wie oben dargelegt braucht eigentlich nur die Wechselwirkung der Sonne mit Trojaner und Planet (zwei unabhängige Zweikörperprobleme) berücksichtigt werden, weil in L4/L5 die Anziehung der Sonne mindestens 1000-fach stärker ist. In dieser Näherung ist sofort klar, dass die Lösung nicht derart "stabil" ist, dass der Winkelabstand von Planet und Trojaner gleich bleibt. Der Trojaner läuft bei einer kleinen Abweichung entweder etwas langsamer oder schneller um und wird daher vom Planeten überholt oder holt umgekehrt den Planeten langsam ein. Ein genauere Berechnung ist unsinnig, weil dann konsequenter Weise nicht nur Trojaner und Planet sondern auch die anderen Planeten berücksichtigt werden müssen und zudem sich die Planetenbahnen in Wahrheit keine Kreise (siehe Kepler-Gesetze). 84.59.49.249 22:34, 12. Jun. 2007 (CEST)
- Um zu berurteilen, ob das mathematisch korrekt ist wäre schon ein genaueres Studium des Artikels erforderlich. Das scheint mir jedoch Zeitverschwendung. Das Dreikörperproblem, schon gar nicht ein eingeschränktes mit Kreisbahnen und ganz bestimmten Punkten, ist nämlich wie oben erläutert keineswegs ausreichend für eine wirklich exakte Berechnung, weil die Wechselwirkungen aller Planeten berücksichtigt werden müssen und selbstverständlich auch die Abweichungen von Kreisbahnen zu berücksichtigen sind. Trotzdem ist völlig klar, dass die Zweikörpernäherung innerhalb weniger Umläufe nur um ein paar Prozent von der realen abweicht abweichen kann. Daher ist klar, die Bahnen in L4/L5 sind nicht stabil. 84.59.63.145 23:29, 12. Jun. 2007 (CEST)
- tut mir leid, aber du bist dumm! anders kann ichs leider nicht ausdrücken. du weigerst dich, genauere informationen zu diesem problem einzuholen, obwohl dir mehrfach gesagt wurde, das deine argumente schlicht und einfach falsch sind. wieso kommst du auf die absurde idee, das zweikörperproblem wäre eine angemessene näherung für die trojanerbewegung? wenn du zu dumm/faul bist, um dich mit der physik des problems zu beschäftigen, dann lass es bitte gleich sein, und geh uns hier nicht auf die nerven.--moneo d|b 12:36, 13. Jun. 2007 (CEST)
- Die Lösung des Zweikörperproblems für die Planeten wird durch die Kepler-Gesetze beschrieben. Die Behauptung die Keplerschen Gesetze seinen ungeeignet die Bahnen der Planeten zu beschreiben, habe ich auch noch nie gehört. Diese Gesetze sind vielmehr eine sehr gute Näherung, weil die Masse der Sonne sehr viel größer als die der Planeten ist. Daher ist die gegenseitige Anziehung der Planeten zu vernachlässigen und ebenso die Mitbewegung der Sonne. Aus exakt den gleichen Gründen ist auch für die "Trojaner" in L4 und L5 die Keplersche Zweikörperlösung ebenfalls eine sehr gute Nährerung. 84.59.143.205 16:45, 13. Jun. 2007 (CEST)
- genau da liegt dein problem. du kannst vielleicht in erster näherung die anziehung der planeten aufeinander vernachlässigen und ihre bewegung durch kepler-bahnen beschreiben. aber bei trojaner funktioniert das nicht. wenn du das zweikörperproblem benutzt und nur sonne und trojaner berücksichtigst, dann vernachlässigst du die interaktion zwischen jupiter und dem trojaner komplett. und auf die kommt es an... mach doch einfach ein experiment: besorg (oder programmier) dir einen numerischen integrator, der die bewegungsgleichungen des n-körper problems löst (z.b. mercury6: hier), besorg dir die aktuellen daten von jupiter und einem l4-trojaner (z.b. von hier) und schau dir an, wie sich die bahn des trojaners im laufe der zeit ändert... du kannst wahrscheinlich einige milliarden jahre integrieren (wenn dein computer das packt) ohne das du eine nenneswerte instabilität findest (natürlich gibts ausnahmen, aber das ist eine andere geschichte)... aber ich nehm nicht an, das du das machen wirst, oder? schon witzig, das du meinst, das sich knapp 300 jahre physikalisch/astronomisch/mathematische forschung einfach durch ein paar von dir hingeschluderte formeln widerlegen lassen...--moneo d|b 17:05, 13. Jun. 2007 (CEST)
- Die Lösung des Zweikörperproblems für die Planeten wird durch die Kepler-Gesetze beschrieben. Die Behauptung die Keplerschen Gesetze seinen ungeeignet die Bahnen der Planeten zu beschreiben, habe ich auch noch nie gehört. Diese Gesetze sind vielmehr eine sehr gute Näherung, weil die Masse der Sonne sehr viel größer als die der Planeten ist. Daher ist die gegenseitige Anziehung der Planeten zu vernachlässigen und ebenso die Mitbewegung der Sonne. Aus exakt den gleichen Gründen ist auch für die "Trojaner" in L4 und L5 die Keplersche Zweikörperlösung ebenfalls eine sehr gute Nährerung. 84.59.143.205 16:45, 13. Jun. 2007 (CEST)
- Häh – welche Formeln habe ich denn hier hingeschleudert und welche seit 300 Jahren gesammelten fundamentalen Erkenntnisse haben denn mit L4 und L5 zu tun ? 84.59.54.148 21:52, 13. Jun. 2007 (CEST)
ich rede von den formeln, die du hier ständig postest und mit denen du die instabilität der lagrange-punkte "beweisen" willst... und die stabilität der lagrange-punkte wird seit etwa 300 jahren (da hat Joseph-Louis_Lagrange nämlich gelebt) untersucht. schau mal im ads nach - da findest du 118 artikel aus den letzten 100 jahren, die sich hauptsächlich mit den lagrange-punkten befassen - und das ist nur ein kleiner ausschnitt aus der kompletten menge an forschungsarbeit - meinst du wirklich, diese leute wüssten alle nicht, was sie tun?--moneo d|b 22:14, 13. Jun. 2007 (CEST)
- Ach – du meinst meine eigene Herleitung für die Lagrangepunkte L4,L5. Damit habe ich ja zunächst einmal nur gezeigt, dass bei geeigneter Winkelgeschwindigkeit tatsächlich drei Massen auf den Eckpunkten eines gleichseitigen Dreiecks um ihren gemeinsamen Schwerpunkt kreisen können. Eigentlich genügt es für die Herleitung schlicht Isaac Newtons Kraftgesetz für drei Massen aufzuschreiben und die Abstände alle gleich einem festen Wert R zu setzen. Die Sache funktioniert sogar völlig unabhaängig von der Größe der drei Massen. Um zu zeigen, dass L4/L5 nicht stabil sein können, reicht es das Zweiköperproblem (siehe Kepler-Gesetze) zu betrachten, wie oben ausgeführt. 84.59.58.234 01:55, 14. Jun. 2007 (CEST)
- Nein, reicht es eben nicht!! nochmal: das zweikörperproblem ist keine geeignete näherung um die bewegung in der umgebung der lagrange-punkte zu untersuchen! das was du sagst ist falsch! wieso hast du eigentlich so ein problem damit, zu akzeptieren, das du falsch liegst? naja - ich hätt mich gar nicht erst auf die diskussion mit dir einlassen sollen - aber ich hab mir halt eingebildet, das du eventuell doch an ein paar fakten interessiert bist - aber an deinen scheuklappen kommt wohl niemand vorbei.--moneo d|b 09:01, 14. Jun. 2007 (CEST)
- Ach – du meinst meine eigene Herleitung für die Lagrangepunkte L4,L5. Damit habe ich ja zunächst einmal nur gezeigt, dass bei geeigneter Winkelgeschwindigkeit tatsächlich drei Massen auf den Eckpunkten eines gleichseitigen Dreiecks um ihren gemeinsamen Schwerpunkt kreisen können. Eigentlich genügt es für die Herleitung schlicht Isaac Newtons Kraftgesetz für drei Massen aufzuschreiben und die Abstände alle gleich einem festen Wert R zu setzen. Die Sache funktioniert sogar völlig unabhaängig von der Größe der drei Massen. Um zu zeigen, dass L4/L5 nicht stabil sein können, reicht es das Zweiköperproblem (siehe Kepler-Gesetze) zu betrachten, wie oben ausgeführt. 84.59.58.234 01:55, 14. Jun. 2007 (CEST)
- Also noch ein letzter Versuch es dir begreiflich zu machen. Wie ich für die Lagrangepunkte L4, L5 unter Berücksichtigung aller drei Massen (für diesen Spezialfall ist das Dreiköperproblem ja einfach zu lösen) hergeleitet hatte errechnet sich die Umlauffrequenz aus der Gesamtmasse. Da die Masse des Trojaners vernachlässigbar klein ist (dies wird ja immer angenommen, obgleich die Voraussetzung gar nicht erforderlich ist) werden Planet und Sonne von dem Trojaner nicht merklich beeinflusst. Das Ergebnis stimmt folglich praktisch mit der Zweikörpernäherung überein. Warum sollte es für benachbarte Punkte nicht so sein ? Falls der Trojaner auf einer Kreisbahn mit 99 % des "L5-Radius" umläuft, ist er nach dem dritten Keplerschen Gesetz deutlich schneller (die Umlaufzeit ist mehr als ein Prozent kürzer), die Störung durch den Planeten ist mindestens eine Größenordnung geringer. Es gibt keinen Grund daran zu zweifeln, dass der Trojaner schneller umläuft (etwa 1,5 Prozent kleinere Umlaufzeit) und daher seine relative Position zum Planeten langsam, im Laufe mehrerer Umläufe, verändert. 84.59.129.113 11:53, 14. Jun. 2007 (CEST)
- und nochmal ein versuch, es dir begreiflich zu machen... den einfluss des trojaners auf sonne und jupiter kannst du vernachlässigen - aber du musst den kombinierten einfluss von sonne und jupiter auf den trojaner untersuchen - und das machst du eben nicht! drum stimmt auch dein ergebnis nicht!
- ich habe mit tatsächlich die mühe gemacht - so wie oben beschrieben - die bahn des trojaners achilles für die nächsten 10 millionen jahre (etwa 8 millionen umläufe) zu berechnen - die ergebnisse siehst du auf den beiden bildern. sowohl die bahn selbst als auch die änderung der großen halbachse des asteroiden verläuft absolut stabil--moneo d|b 13:39, 14. Jun. 2007 (CEST)
- Ja klar, der Trojaner bleibt eben nicht in der Nähe von L4 und L5 und kommt Jupiter hin und wieder relativ nahe. Dann ist der Einfluß von Jupiter realtiv groß und lenkt ihn aus der Keplerbahn. Jupiter und Sonne sind davon ziemlich unbeeindruckt. Die Bahn des Jupiter ändert sich daher kaum merklich, während der Trojaner ziemlich chaotisch seine Keplerparameter ändert. Ich kann natürlich nicht beurteilen, ob es wirklich richtig gerechnet ist. Aber es könnte schon stimmen. Was willst du mir damit jetzt sagen ? 84.59.48.254 15:26, 14. Jun. 2007 (CEST)
- also zeig mir bitte erstmal, wo hier irgendetwas chaotisch ist? ein chaotischer orbit sieht völlig anders aus. was ich dir damit sagen will? das es ein bisschen sinnfrei ist, ein objekt, dessen bahn sich 10 millionen jahre lang kaum ändert (ich hätte auch für 100 millionen oder 1 milliarde jahre integrieren können - hatte nur die zeit nicht), als "instabil" zu bezeichnen...--moneo d|b 15:41, 14. Jun. 2007 (CEST)
- Ja klar, der Trojaner bleibt eben nicht in der Nähe von L4 und L5 und kommt Jupiter hin und wieder relativ nahe. Dann ist der Einfluß von Jupiter realtiv groß und lenkt ihn aus der Keplerbahn. Jupiter und Sonne sind davon ziemlich unbeeindruckt. Die Bahn des Jupiter ändert sich daher kaum merklich, während der Trojaner ziemlich chaotisch seine Keplerparameter ändert. Ich kann natürlich nicht beurteilen, ob es wirklich richtig gerechnet ist. Aber es könnte schon stimmen. Was willst du mir damit jetzt sagen ? 84.59.48.254 15:26, 14. Jun. 2007 (CEST)
- Es geht hier doch um die Stabilität von L4 und L5. Nach deiner Rechnung bleibt der Trojaner, der sich zufällig mal in der Nähe dieser Punkte aufhält ebenen nicht dauerhaft in der Nähe dieses Punktes. Daher kann von Stabilität dieser speziellen Dreikörperlösung keine Rede sein. Es hat schließlich keiner behauptet der Trojaner würde auf die Sonne stürzen oder das Sonnensystem verlassen. Der Trojaner taucht aber immer mal wieder in der Nähe der Punkte L4 und L5 auf. Daher ist es kein Wunder, dass in der Tat solche Objekte gefunden wurden. 84.59.56.99 10:08, 15. Jun. 2007 (CEST)
- also: "stabilität der langrange-punkte" bedeutet folgendes: ein körper, der sich in der nähe von L4 oder L5 aufhält, wird sich auch weiterhin immer in der nähe dieser punkte aufhalten. "instabilität" (wie bei L1,2,3) bedeutet, das sich ein körper, in der nähe von z.b. L1 durch die wirkendene störungen im laufe der zeit immer weiter von diesem punkt entfernen wird. und es lässt sich eben berechnen (siehe den link, den ich oben gepostet habe), das die punkte L4 und L5 in diesem sinne stabil sind. unter gewissen bedingungen natürlich (das massenverhältnis der primärkörper muss kleiner als 1/25 sein - und beliebig weit kann sich ein körper natürlich auch nicht vom lagrangepunkt entfernen. ich hab noch ein bild dazu hochgeladen: da siehst du in einem diagramm, in dem, abhängig von der anfänglichen mittleren länge der trojaner und der anfänglichen exzentrizität ihrer bahnen dargestellt wird, ob die bahnen stabil (weiss) sind - also für lange zeiträume in der nähe der lagrangepunkte bleiben - oder instabil (schwarz) - also irgendwann die umgebung der lagrange-punkte verlassen und keine trojaner-bewegung mehr ausführen. (die beiden linien im diagramm zeigen die position der lagrange-punkte - L4 bei 60 grad und l5 bei 300 grad an (jupiter befindet sich bei 0 grad). ein trojaner um l4 bzw. l5 kann sich also (abhängig von der bahnexzentrizität) durch aus um bis zu tw. ~40 grad vom lagrangepunkt entfernen und immer noch stabil sein - d.h. in einem mitrotierendem koordinatensystem bewegt sich der trojaner auf einer bahn um den lagrangepunkt. ich glaube, das problem bei dieser ganzen diskussion ist, das du eine andere definition des begriffs "stabilität" hast...--moneo d|b 10:50, 15. Jun. 2007 (CEST)
Man kann die L4- und L5-Bereiche als Potentialmulden auffassen.
Wenn sich nun zahlreiche kleine Körper in diesen Potentialmulden umher
bewegen, und sich gegenseiteig geringfügig gravitativ beeinflussen,
dann kann es zu einem Vorgang kommen, der der Verdunstungs-Kühlung entspricht.
Ein Körper könnte rein zufällig viel kinetische Energie von einigen anderen
Körpern erhalten, und aus der Potentialmulde geschleudert werden.
Nach einigen solcher Vorgänge ist die mittlere kinetische Energie der
in der Potentialmulde verbliebenen Körper etwas geringer geworden,
so dass für diese im Laufe der Zeit die Wahrscheinlichkeit absinkt,
ebenfalls aus der Potentialmulde zu entkommen.
Karl Bednarik 11:28, 17. Jun. 2007 (CEST).
Frage zu Abschnitt 2
Was genau ist unter "gegenseitige tangentiale Anziehungen" verstehen, die sich dann aufheben? Tangential heißt für mich am Rand eine Kreises = am Rand des Querschnitts einer Kugel. Massen ziehen einander aber – idealisiert – im Schwerpunkt an. Und der liegt bei einer – idealisierten – sphären-homogenen Kugel (soll heißen: in gleichem Abstand vom Mittelpunkt herrscht gleiche Dichte) in der Kugelmitte, nicht an deren Oberfläche. Wie kommt da eine Tangente ins Spiel? Oder interpretiere ich da etwas falsch?
Soll das einfach aussagen, dass sich Gravitation und Zentrifugalkraft aufheben und sich dadurch ein stabiles Gleichgewicht einstellt? Aber warum dann diese, zumindest für mich, seltsame Formulierung? --Geri, 10:12, 13. Jan. 2008 (CET)
- Das soll heißen, dass der Kraft-Vektor in zwei Komponenten zerlegt wird und diese einzeln betrachtet werden. Und zwar ein Komponente in radialer Richtung (das heißt von den einzelnen Körpern aus in Richtung des gemeinsamen Massenzentrums) und eine in tangentialer Richtung (das heißt alles, was senkrecht zur radialen Richtung steht) In dem betrachteten Fall mit den drei gleich großen Massen heben sich die tangentialen Komponenten dann eben genau auf. Für die radialen Komponenten gilt genau wie du schon schriebst, dass hier Gravitations- und Zentrifugalkraft gleich groß sind. --GluonBall 13:40, 13. Jan. 2008 (CET)
Lesenswert-Diskussion vom 17.-24.12. 2008 (erfolgreich)
Die Librations- oder Lagrange-Punkte sind die nach Joseph-Louis Lagrange benannten Gleichgewichtspunkte des eingeschränkten Dreikörperproblems der Himmelsmechanik. An diesen Punkten im Weltraum heben sich alle Gravitationskräfte benachbarter Himmelskörper und die Zentripetalkraft der Bewegung gegenseitig auf.
Lagrange konnte beweisen, dass das im Allgemeinen analytisch nicht lösbare Dreikörperproblem für einige Spezialfälle des eingeschränkten Dreikörperproblems doch analytisch lösbar ist: Für zwei umeinander kreisende Körper gibt es fünf solche Lagrangepunkte, in denen sich ihre Gravitationskraft und die Zentripetalkraft auf einen dritten Körper mit im Verhältnis zu den anderen beiden verschwindend kleiner Masse aufheben, so dass er in diesen Punkten in Bezug auf die anderen beiden Körper immer denselben Ort einnimmt.
- Pro Meiner Meinung (als Hobby-Astronom) nach ein sehr guter Artikel und absolut lesenswert für Personen mit Interesse für astronomische Beobachtung. Zaesh 08:21, 17. Dez. 2008 (CET)
- Für mich als Laien ist der Artikel überraschend verständlich und gut geschrieben. Trotzdem erfüllt der Artkel meiner Meinung nach nicht die Kriterien für Lesenswerte Artikel. Inhaltlich vermisse ich Angaben zum geschichtlichen Ablauf. Wann hatte Lagrange seine Lösung des Dreikörperproblems veröffentlicht? Hatte die Astronomie sofort das Modell übernommen? Wann begann man nach Himmelskörpern an den Lagrange-Punkten zu suchen? Diese Fragen werden leider auch in den Artikeln zu Joseph-Louis Lagrange und dem Dreikörperproblem nicht beantwortet, einzig der Artikel Trojaner (Astronomie) gibt Hinweise auf die geschichtliche Entwicklung. Darüber hinaus besitzt der Artikel formale Mängel. Nicht nur, dass Aussagen nicht durch Einzelnachweise belegt sind, es findet sich am Ende kein einziger Hinweis auf weiterführende Literatur. Ein Artikel zu so einem naturwissenschaftlich bedeutenden Thema kann nicht einfach nur durch Weblinks belegt sein. Daher Kontra --Andibrunt 14:23, 18. Dez. 2008 (CET)
- Sehe ich genauso wie Andibrunt, gedruckte Quellen und Einzelnachweise für z.B. die Staubwolken sehe ich bei einem naturwissenschaftlichen Artikel als notwendig an. Ein paar Stellen finde ich zudem noch etwas holprig. So wirkt der dritte Absatz der Einelitung auf mich etwas angesetzt ("Muss man irgendwo noch erwähnen"?), was ein labiles und stabiles GGW sind, sollte man für den Laien bei der ersten Erähnung kurz erklären. Dass der Theorieteil ganz ohne Gleichungen auskommt, schreckt den nicht-ganz Laien etwas ab, zumindest ein Diagramm wie in en für L4 wäre nett. Zur Geschichte steht in der en-Version, dass die ersten drei Lagrange-Punkte schon von Euler beschrieben wurden, sowas würde definitiv reingehören! Insgesamt also noch Kontra -- Cymothoa Reden? 14:57, 18. Dez. 2008 (CET)
- Neutral Mir fehlt z.B. noch das Jahr und die Publikation in der Lagrange seinen Beweis geführt hat. --Succu 16:31, 18. Dez. 2008 (CET)
Noch Neutral, mit Tendenz zuPro. Ah super, wieder ein Artikel mit Astronomie Bezug. ;) 2 Fragen: Also auf L4 und L5 der Erdbahn befindet sich "nichts nennenswertes". Hat es Sinn, dort Sonden oder Teleskope zu installieren? Wie groß ist physikalisch so ein Lagrange Punkt der Erdbahn, welcher Bereich oder Durchmesser deckt er ab? Durchmesser einige km oder einige Tausende? --FrancescoA 11:44, 19. Dez. 2008 (CET)
- @FrancescoA, du weist schon was das Wort Punkt bedeute oder? Vorallem wen es sich hier um eines Pysikalischen Phänomen des Kräftegleichgewicht handelt (Massenpunkt). Dessen Lage bekantlich rechnerisch auf Grundlagen der Geometrie errechnet wird (Punkt (Geometrie)). Es kann keine Ausdehunung geben, da selbst die kleinset Abweichung eine Ungleichgewicht in eine Richtung ergibt (auch wen diese ggf erst nach Jahrtaustenden sich bemerkbar macht).
- Ja (ich bin hier Laie), nur ich meinte: Wie groß ist etwa der Bereich, in dem man Objekte installieren könnte, um stabil an Ort und Stelle zu verbleiben (oder verstehe ich das ganze etwas falsch?). BTW: Wer hat eigentlich den Artikel hier als lesenswert vorgeschlagen? --FrancescoA 12:04, 19. Dez. 2008 (CET)
- Hast du schon mal auf der Diskusionseite des Artikels vorbeigesschaut DiskussionLagrange-Punkt. Dort wurde die Frag auch schon gestellt, und auch beatwortet. Um die Punkte (vorallem 4 und 5) sind labile Bahnen möglich. Aber eben wie es der Name schon sagt stabil ist was anderes. Jeder Lagrange-Punkt in unserem Sonnesystem eiert eh, in dem Sinn sind eh nur labile Bahnen möglich (wobei eben gerade die Störungen der anderen Planeten es sein können, die es den Obiekten ermöglichen sich da zu halten). Zu Zweiterfrage: Zaesh -- Bobo11 12:15, 19. Dez. 2008 (CET)
- Danke für die Klarstellung. --FrancescoA 12:21, 19. Dez. 2008 (CET)
- Hast du schon mal auf der Diskusionseite des Artikels vorbeigesschaut DiskussionLagrange-Punkt. Dort wurde die Frag auch schon gestellt, und auch beatwortet. Um die Punkte (vorallem 4 und 5) sind labile Bahnen möglich. Aber eben wie es der Name schon sagt stabil ist was anderes. Jeder Lagrange-Punkt in unserem Sonnesystem eiert eh, in dem Sinn sind eh nur labile Bahnen möglich (wobei eben gerade die Störungen der anderen Planeten es sein können, die es den Obiekten ermöglichen sich da zu halten). Zu Zweiterfrage: Zaesh -- Bobo11 12:15, 19. Dez. 2008 (CET)
- Ja (ich bin hier Laie), nur ich meinte: Wie groß ist etwa der Bereich, in dem man Objekte installieren könnte, um stabil an Ort und Stelle zu verbleiben (oder verstehe ich das ganze etwas falsch?). BTW: Wer hat eigentlich den Artikel hier als lesenswert vorgeschlagen? --FrancescoA 12:04, 19. Dez. 2008 (CET)
- Pro, wobei das Thema einfach ein gewissen Vorwissen voraussetzt. Ich hab nicht das Gefühl, dass man den gesamten Artikel omA-tauglich hinkrigt.Bobo11 11:59, 19. Dez. 2008 (CET)
- Pro, schöner Artikel, gut verständlich, ausgesprochen gut bebildert, der kaum eine Frage offenlässt. Meiner Meinung nach nahe am Exzelenten. Für Exzellenz könnte man aber tatsächlich mehr über den geschichtlichen Ablauf hinzufügen. -- IKAl 18:36, 20. Dez. 2008 (CET)
Pro Es mag seltsam erscheinen, dass ich ein Latte von Verbesserungsvorschlägen anhänge, aber im Kern finde ich die Aufgabe dieses mathematisch-astronomische Problem omA-tauglich darzustellen gut gelöst. Auch die Belegung des Artikels sehe ich als gegeben, wenn auch selbst für ein Lesenswert nur gerade ausreichend. Trotzdem noch ein paar Wünsche für eine Überarbeitung.
- In der Einleitung könnte das eingeschränkte Dreikörperproblem noch mit einem Satz erklärt werden. Dafür ist der letzte Satz völlig verzichtbar, da dies zum Lemma nichts beiträgt.
- Unter Lage der Punkte wird etwas zur Stabilität bzw. Labilität der Punkte ausgesagt was mit der Lage nichts zu tun hat und hier erst mal nur fragen aufwirft. s.u.
- Wieso etwas einen LP umkreisen kann wird erst im Letzten Abschnitt erklärt, obwohl es auch dort nicht ausdrücklich Thema ist. Da sich in den LP die Anziehungskräfte aufheben, scheint das bis dahin rätselhaft, da Körper ja sonst um "Schwerkraftsenken" kreisen. Vielleicht sollte an entsprechender Stelle zumindest auf den letzten Abschnitt verwiesen werden.
- Ähnliches gilt für die schon früh genannte Stabilität bzw. Labilität der Geleichgewichte (s.o.). Dabei ist die Stabilität der L4 und 5 weniger verständlich gemacht als die Labilität der anderen Punkte. Was soll ein (CF-Attraktor)? Leider führt der Link auf Attraktor zu kaum verständlicher Mathe-lyrik. Wie kommt es zu dieser seltsamen Zahl 24,96?
- Es wird am Anfang nicht immer deutlich gemacht, dass das Erde-Sonne-System als Beispiel benutzt wird. Da müsste also hin und wieder noch ein z. B. eingefügt werden. Dabei würde mich noch interessieren in wie weit dieses Beispiel überhaupt exemplarisch ist, da ja der Mond als Störfaktor hinzutritt.
- Mit "Beispiel" wird jeweils ein Beispiel für die Nutzung der LP oder dort vorhandener Objekte gegeben aber kein Beispiel zu dem LP an sich, was ja auch nicht notwendig ist. Beispiel ist hier also irgendwie das falsche Wort.
- Die "vereinfachte Darstellung" bricht gegen Ende in seiner Verständlichkeit stark ein. (großes Massenverhältnis? Wirken am Schwerpunkt vorbei? chaotische Funktion hoher Amplitude? Wieso hat die Erde LPs wenn ihre Auslenkung der Sonne doch eigentlich nicht ausreichend ist bzw. von der Jupiters überlagert wird?)
- Gibt es eine Notwendigkeit dafür das L1 und L2 etwa gleich weit vom kleineren Körper entfernt sind oder ist das ein Sonderfall der Erde?
- (Das gehört hier nicht hin, aber wieso das Hufeisenumlaufbahn heißt bleibt mir ein großes Rätsel. Die Form ähnelt keinem mir bekannten Hufeisen. Das auf der Grafik dargestellte ist eindeutig eine Wendel/Helix.)--WerWil 14:13, 22. Dez. 2008 (CET)
- Pro, verständlich ein nicht ganz einfaches Thema dargestellt.--wdwd 22:07, 22. Dez. 2008 (CET)
- Pro, kann mich meinem Vorredner nur anschließen. --WLinsmayer 09:04, 23. Dez. 2008 (CET)
Der Artikel in dieser Version] ist Lesenswert mit 7 Pro, 1 Neutral, 2 Contra. --Vux 02:12, 24. Dez. 2008 (CET)
L2 Schatten?
Liegt der L2 im Kernschatten der Erde? --Itu 04:01, 12. Jan. 2011 (CET)
- Gute Frage, die Antwort ist "jein" - er wäre (aufgrund der zufälligen geometrischen Übereinstimmung) knapp drin, wenn die Erde keine Atmosphäre hätte. Streulicht erreicht L2 dennoch, ebenso genügen kleine Umlaufbewegungen, um den geometrischen Kernschatten zu verlassen. --Raumfahrtingenieur 14:01, 8. Mär. 2011 (CET)
Lage von L1 und L2
Im Punkt L1 auf der geraden Verbindungslinie von Erde und Sonne ist die Zentrifugalkraft gleich der Differenz der Gravitationskräfte der beiden Himmelskörper
Wobei die Abstände von L1 und der Erde zur Sonne sind.
Mit der Beziehung
kann man schließlich ableiten
wobei x als definiert wurde. Die Gleichung kann nicht elementar nach x aufgelöst werden. Die Berechnung von x kann jedoch auf die Berechung einer Nullstelle der Funktion
mit den Newton-Verfahren zurückgeführt werden.
Falls mit sehr viel kleiner eins und die Sonnenmasse viel größer als die Planetenmasse, können Terme mit und vernachlässigt werden. Es folgt:
Da die dreifache Sonnenmasse etwa eine Million mal die Erdmasse ist, ergibt sich für ein Wert von 0,01. Der Abstand von L1 zur Erde beträgt also etwa 0,01 AE oder 1,5 Millionen Kilometer.
Die Berechung der Lage von L2 ist vollkommen analog durchzuführen. Es ändert sich nur ein Vorzeichen, da jetzt die Gravitationskräfte von Erde und Sonne in die gleiche Richtung wirken. L2 ist ebenfalls etwa 1,5 Millionen Kilometer von der Erde entfernt.
Der Abstand L1 und L2 ist etwa der größte mögliche Abstand eines Mondes der die Erde umkreist und nicht die Sonne. Analog kann auch für die anderen Planeten die größte mögliche Halbachse für eine Mondbahn berechnet werden.
Stabilität der Bahn in der Nähe von L1
Bewegt man sich in dem rotierenden Koordinatensystem auf der Verbindung L1 zu Planet in Richtung zum Planeten stehen Fliehkraft und Gravitationskräfte nicht mehr im Gleichgewicht und die Anziehung des Planten überwiegt. Falls die Probemasse sich in Richtung Sonne bewegt über wiegt die Anziehung der Sonne. Daher scheint der Schluss nahezuliegen, dass diese Lage instabil sei und nach einer kleinen Störung die Probemasse entweder in die Sonne oder auf den Planeten stürzt.
Dies ist jedoch völlig falsch. Ein Körper der sich auf der Verbindungslinie in dem mitrotierenden Koordinatensystem bewegt, ändert nämlich seinen Drehimpuls. Ein Crashkurs mit Sonne oder Planet würde die Drehimpulserhaltung verletzen. Der Körper erfährt im rotierten Koordinatensystem, neben der Fliehkraft, eine weitere Scheinkraft, die Corioliskraft, wenn er sich auf der Verbindungslinie bewegt, die ihn von dieser ablenkt.
- Damit dürften die Gründe für das im Text öfter erwähnte „Umkreisen des L-Punktes x“ umrißen sein. IMO sollte dieses Verhalten, diese Summe physikalischer Auswirkungen da noch erleutert (und natürlich mit den entsprechenden Stellen verlinkt; vielleicht auch mit dem Anreißen von Themen wie „Sateliten werden durch Bremsen schneller“), denn die „normale Erwartung“ (der menschliche Blick aus einem nur scheinbar passenden Blickwinkel) geht ja in eine andere Richtung.
- Vielleicht sollte man überhaupt mal überlegen, zu entsprechenden Themen (also nicht nur hierzu; mir fallen da jetzt zwar nur physikalische Effekte ein, aber wer weiß …) Ableger bzw. Anhänge unter dem Motto „das hätten Sie nicht gedacht“ oder „Physik (scheinbar) verrückt“ zu gestalten. Wobei dies hier z.B. eine Art Schnittmenge zwischen Zentripetalkraft, Corioliskraft und dem besagten Umkreisen wäre.
Was heißt eigentlich stabil
Im Internet kursieren etliche Abhandlungen zur Stabilität der Lagrange-Punkte ohne das überhaupt klar wird, was eigentlich unter der Stabilität des Gleichgewichts zu verstehen sei. Falls man eine Bahn als stabil ansieht, sofern durch eine kleine Abweichung weder Sonne und Planet noch die Probemasse mit einem der anderen Himmelskörper kollidieren oder sich unbegrenzt weit von einander entfernen sind die Bahnen in der Nähe der Gleichgewichtspunkte L1 und L2 als stabil zu betrachten. Eine Kollision mit der Sonne oder eine wesentlich sonnennähere oder sonnenfernere Bahn widerspräche in jedem Fall Energie- und Drehimpluserhaltung. Eine Kollision mit dem Planeten wäre für Trojaner, also in der Nähe der der Punkte L4 oder L5 aber denkbar. L4 und L5 sind ganz in der Nähe der Umlaufbahn und die Störung durch den Planeten ist gering. Die Trojaner umlaufen den Jupiter also auf fast denkungsgleichen Bahnen. Wenn die Umlaufzeiten sich geringfügig unterscheiden wird der Trojaner den Jupiter oder umgekehrt der Jupiter den Trojaner irgendwann überholen, dabei kommt der Trojaner eventuell in der Nähe von L3 vorbei. Im Extremfall kommt es beim Überholen zum Crash oder der Trojaner bzw. ehemalige Trojaner wird als Mond eingefangen. Die Bahnen in der Nähe von L4 und L5 und auch L3 sind daher als extrem instabil zu bezeichnen. In L1 und L2 bleibt der Abstand zum Planeten nicht konstant es besteht aber keine Crashgefahr, da sich die Punkte im Phasenraum nahe einer stabilen Mondbahn befinden. --LAP5 12:28, 18. Aug 2006 (CEST)
- nochmal: wenn du meinst, hier jedes detail in frage stellen zu müssen, dann erwarte ich auf von dir das du detailliertes wissen über die thematik hast... und die hast du nicht... hast du das kapitel aus dem buch, das ich dir geschickt habe gelesen? oder dich sonstwie über die thematik informiert? anscheinend nicht - ansonsten würdest du z.b. nicht schreiben, das die trojaner auf "fast deckungsgleichen bahnen" umlaufen - denn das ist falsch! stabilität: lies mal was zum thema nullgeschwindigkeitskurven... oder zum potential des eingeschränkten dreikörperproblems...--moneo d|b 14:30, 18. Aug 2006 (CEST) p.s. und was soll ein "punkt im phasenraum nahe einer stabilen mondbahn" sein???--moneo d|b 14:30, 18. Aug 2006 (CEST)
- ich verstehe es sogar, und daher an LAP5 meine einfache Erklärung: "stabil" meint, dass ein Körper am lagrange-Punkt ohne Korrekturantrieb ewig sein kann. Daher finden sich an L1 un L2 keine Himmelskörper, sehr wohl jedoch an L3 und L4. SOHO hat daher Korrekturantriebe (er kreist 1x in 6mon um L1 von sonne/erde). --Ulfbastel 10:04, 1. Sep 2006 (CEST)
Bitte "stabiles" Gleichgewicht nicht mit einer stabilen Bahn gleichsetzen. Ein stabiles Gleichgewicht setzt nur ein (relatives) Minimum eines Energieprofils voraus. Diesem Energieprofil liegt das (mit dem Planeten mit-)rotierende Bezugssytem zugrunde.
Im übrigen befinden sich die Punkte L1/L2/L3 in labilen Gleichgewichten ("instabile" Gleichgewichte gibts nicht), die im dreidimensionalen Energieprofil Sattelpunkten entsprechen. Die Problematik für die Trojaner liegt darin, daß sie sich nicht exakt am Lagrange-Punkt befinden, sondern nur in seiner Nähe. Wenn sich L4/L5-Trojaner nicht zu weit vom Lagrange-Punkt entfernen, kreisen sie (im rotierenden Bezugssytem) nierenförmig um diesen Punkt. Entfernen sie sich zu weit, driften sie ab, zB in Hufeisenbahnen. Sowohl Trojanerbahnen als auch Hufeisenbahnen sind im Dreikörperproblem als "stabil" zu betrachten, auch wenn sie im Grenzfall in der Realität über lange Zeiträume hinweg chaotisch sind, also nicht berechenbar. Für L1/L2/L3-Trojaner ist Sache noch schwerer, da bereits eine winzige Ablenkung vom Lagrangepunkt weg führt. Und diese ist im Sonnensytem immer gegeben, da die Idealbedingungen für einen Lagrangepunkt real nicht gegeben sind (mehr als nur ein Dreikörperproblem, keine Punktmassen, keine verschwindende Masse des Trojaners, seine Inklination, ...). Daher SOHO's Korrekturantriebe, wie schon Ulfbastel sagte. --Gérard 23:31, 15. Okt. 2006 (CEST)
- Genau, es gibt unzählige kleine Abweichungen vom Ideal, den speziellen Lösungen des Dreikörperproblems nach Lagrange. Die Bahnen sind keine Kreise sondern (annähernd) Keplerellipsen, liegen nicht in einer Ebene und die Abstände stimmen nie ganz exakt. Es gibt zudem weit mehr als drei Massen, die zu berücksichtigen sind. Dies alles gilt aber auch für L4 und L5. Ein Trojaner wird daher in der Realität niemals exakt gleich schnell wie der Planet umlaufen. Daher bleibt auch dort die Konstellation nicht stabil. 84.59.134.67 12:30, 13. Jun. 2007 (CEST)
Gegenerde am Lagrange-Punkt L3
So wie ich das verstanden habe, bleibt ein Objekt doch nur dann am Lagrange-Punkt, wenn seine Masse "verschwindend gering" ist, oder? Das wäre ja bei einer "Gegenerde" nicht der Fall. Wären dann nicht beide Erden an einem instabilen Punkt, weil ja die "Gegenerde" die Erde genauso beeinflussen würde wie umgekehrt?
Ich kenne eine "Gegenerde" nur aus einem Urmel Buch. Da wurden Lagrange-Punkte komischerweise nicht weiter behandelt.
Grüße aus San Sebastian,
Oliver
Bei einer hypotetischen Gegenerde, die auf der Erdbahn genau gegenüber der Sonne umläuft, kann die Anziehung dieser beiden Planeten praktisch vernachlässigt werden. Die Anziehungskraft der Sonne wäre millionenfach größer und die Anziehung durch den Jupiter noch erheblich größer als die gegenseitige Anziehung. Entsprechend läge L3 fast genau auf der Erdbahn. Rein theoretisch wäre es natürlich denkbar, dass zwei Massen um ein Zentralgestirn derartig umlaufen. Aus Sicht eines der beiden umlaufenden Objekte ist damit die Anziehung durch das Zentralgestirn scheinbar minimal vergrößert. Die Gegenerde hätte folglich den gleichen Effekt wie eine minimale Zunahme der Sonnenmasse. Es ist jedoch kaum erklärbar wie ein Planet genau in den Punkt L3 gelangen sollte und auch noch exakt die passende Geschwindigkeit erhalten sollte, um dort zu verweilen.
Hallo, bezüglich des L3-Punktes fehlt noch die Beschreibung was sich derzeit dort befindet. Asteroid? Staubwolke? Habe aber leider nirgends einen Artikel gefunden in dem beschrieben wird ob dieser Punkt schonmal beobachtet wurde, jedoch bin ich mir dessen ziemlich sicher. Kann dort überhaupt etwas sein (wegen der Instabilität?)
- nee da kann nichts sein weil instabil--Ulfbastel 10:14, 1. Sep 2006 (CEST)
Bezüglich der Instabilität sollte auch noch erwähnt werden, warum die Librationsbahnen um diese Punkte überhaupt instabil sind. mfg Matthias
- die Bahnen um die Punkte sind aus dem gleichen Grund instabil wie es auch die Punkte L1, L2 und L3 selbst sind: verlässt eine Masse den Punkt bzw. seine Bahnebene, vergrößert sich die Gravitation auf ihn so, dass er nicht wieder zurück (wie bei L4 u nd L5), sondern noch weiter weggezogen wird. Dessen evtl. vorhandene Kreisbahn und Umlaufzeit verkleinert sich dabei und die Bewegung endet 100%ig mit einem Sturz auf einen der beiden großen Himmelskörper.--Ulfbastel 10:17, 1. Sep 2006 (CEST)
Hab mir grad Harald Lesch zu diesem Thema reingezogen und verstehe nicht, was bei L3 (der in dem Video als L2 betitelt wird) eine Aufhebung der Gravitation der Sonne bewirken söllte. Die Erde kann es wohl kaum sein! Natürlich verstehe ich, dass die Sonne an L2 eine derartige Mit-Auswirkung hat, aber bei L3 sehe ich dies nicht, da die Gravitation der Erde verglichen mit der der Sonne einfach zu klein ist. Vielleicht versteht ihr, was ich meine, wenn ich euch noch dieses Vid von Herrn Lesch anschaut.
[edit]Ich muss mich dahingehend korrigieren, dass auch L2 keinen Sinn ergibt, da sich auch hier die gravitativen Kräfte von Erde und Sonne lediglich addieren würden.[/edit]
Gruß (nicht signierter Beitrag von 217.93.175.52 (Diskussion | Beiträge) 08:27, 19. Dez. 2009 (CET))
L1 und L2 verhalten sich zueinander wie die beiden Flutberge der Erde (von denen der eine ja auch auf der mondabgewandten Seite der Erde liegt). 16.3.2011, BJF (nicht signierter Beitrag von 92.206.103.185 (Diskussion) 17:29, 16. Mär. 2011 (CET))
Weitere stationäre Orte
Mir ist aufgefallen, daß es noch weitere stationäre Orte geben muß, beispielsweise relativ zur Erde im luna-stationären Mondorbit in knapp 100000 km Höhe. Theoretisch müßte es doch in jedem Dreikörpersystem einen Lagrange-Orbit um das mittelschwere Objekt herum geben, oder nicht? (nicht signierter Beitrag von 87.170.147.219 (Diskussion) 14:59, 3. Sep. 2010 (CEST))
Lagrange löst das Dreikörper-Problem nur für den Spezialfall, daß der dritte Körper K3, der synchron mit K2 um K1 rotiert, die Masse Null hat (bzw. eine gegenüber K1 und K2 verschwindend geringe Masse). Damit sind Lagrange-Punkte für K3 praktischerweise aus der Welt. Eine nennenswerte Masse für K3 würde nicht nur weitere 5 Lagrange-Punkte (für K3) in die Rechnung einführen, sondern auch Auswirkungen auf die Lage der Lagrange-Punkte von K2 haben - was wohl einer der Gründe für die Hartleibigkeit des allgemeinen 3-Körper-Problems sein dürfte. (Wäre ja aber mal interessant zu sehen, wie die L-Punkte sich verhalten, wenn man eine geringe Masse in z. B. L4 langsam auf Erdformat anwachsen läßt!) 16.3.2011, BJF (nicht signierter Beitrag von 92.206.103.185 (Diskussion) 17:29, 16. Mär. 2011 (CET))
Lage von L3
Im Artikel heißt es, der Lagrange Punkt L3 wäre etwas weiter weg von der Sonne als die Erde. Meine Berechnungen ergeben etwas anderes: L3 ist dichter an der Sonne als die Erde. L3 ist zwar außerhalb der Umlaufbahn der Erde, aber die Erde kreist ja nicht um den Mittelpunkt der Sonne, sondern um den Schwerpunkt von Erde und Sonne. Der Schwerpunkt ist etwas dichter an der Erde als der Sonnenmittelpunkt. So kann L3 außerhalb der Umlaufbahn sein, aber trotzdem dichter an der Sonne als die Erde.
Eine Bestätigung für meine Ansicht habe ich hier gefunden: Lagrangian_point
Gruß Nicolas
--91.5.251.77 17:41, 19. Apr. 2010 (CEST)
Nachtrag: Ich gehe bei meinen Betrachtungen davon aus, dass sich Erde und Sonne auf Kreisbahnen um den gemeinsamen Schwerpunkt bewegen, was nur in erster Näherung, aber nicht tatsächlich, der Fall ist. Ich kann also nicht ausschließen, dass beim tatsächlichen System Erde-Sonne die Verhältnisse doch wieder anders sind.
Der Unterschied zwischen den Abständen beträgt bei meinen Berechnungen auch nur etwas mehr als 260 km.
--91.5.196.53 23:50, 19. Apr. 2010 (CEST)
Kommt immer drauf an, wie weit man in seinem Modell abstrahiert. Tatsächlich bewegt sich die Erde ja nicht auf einer Kreisbahn, sondern auf einem Schlingerkurs um den gemeinsamen Massenmittelpunkt von Erde und Mond. Zwar ist das Dreikörperproblem nicht lösbar (oder jedenfalls ungelöst), aber ich schätze mal, dass die 260 km da schnell unter die Räder kämen.
PädagogischerEros, 10.4.2011 (nicht signierter Beitrag von 92.206.149.218 (Diskussion) 08:09, 10. Apr. 2011 (CEST))
Kräfteverhältnisse
Die Gravitationskräfte heben sich in den Lagrange-Punkten nicht auf - wie sollte das auch bei L3 etwa zugehen? -, sondern addieren sich dergestalt, daß sich ein Körper in einem Lagrange-Punkt eines Planeten mit diesem Planeten synchron um das Zentralgestirn bewegen kann. Wären Körper in Lagrange-Punkten kräftefrei, so würden sie sich geradlinig fort- und also aus dem System hinausbegeben. BJF, 8.3.2011 (nicht signierter Beitrag von 92.206.96.5 (Diskussion) 13:47, 8. Mär. 2011 (CET))
- Genau - es geht um das dynamische Gleichgewicht im bewegten System. Keinesfalls darf man sich die großen Körper als ruhend vorstellen. --Raumfahrtingenieur 14:07, 8. Mär. 2011 (CET)
Mir scheint, das Problem liegt darin, dass hier mathematische, quantitative Behandlung und physikalische, qualitative Erklärung auseinandergehen. Flieh- und Coriolis"kraft" sind - wie man an dem Hauptbeitrag sieht - zweckmäßig für die mathematische Behandlung, aber physikalisch nicht existent. Sie treten als Artefakte (sog. Scheinkräfte)auf, wenn man ein (in diesem Fall im Takt der Erde mit der Sonne im Zentrum) mitrotierendes Bezugssystem verwendet. Wenn das nicht klargestellt wird, kommt ein Leser leicht zu dem Schluss, dass etwa ein Körper in der Nähe von L4 auch von außen betrachtet um L4 rotiere; tatsächlich aber führt er ja - jedenfalls vom Standpunkt eines außenstehenden Betrachters - eine Schlingerbewegung um die Kreisbahn von L4 aus. Und die "Fliehkraft" hebt zwar sehr schön die Zentripetalkraft (Gravitation) auf, nur kann sie das physikalisch nicht leisten, weil es sie physikalisch nicht gibt. Diesen Missverständnissen kann man alle Naselang in den Wissenschaftsseiten von F.A.Z., Süddeutscher e tutti quanti begegnen. Darum hielte ich es für didaktisch zweckmäßig, erst einmal die physikalischen Verhältnisse explizit in ein mathematisches Modell zu übersetzen, und dann die mathematischen Ergebnisse aus dieser Modellbetrachtung in die physikalischen Verhältnisse rückzuübersetzen. PädagogischerEros, 10.4.2011 (nicht signierter Beitrag von 92.206.149.218 (Diskussion) 08:09, 10. Apr. 2011 (CEST))
Entdeckung eines Erdbegleiters
In einem Artikel bei Spiegel Online vom 27.07.2011 wird die Entdeckung eines Erd-Trojaners auf Lagrange-Punkt L4 beschrieben. Da die Nachricht keine Quellenangabe enthält, verweise ich hier nur darauf und ändere den Eintrag nicht umgehend: http://www.spiegel.de/wissenschaft/weltall/0,1518,776974,00.html (nicht signierter Beitrag von 82.113.99.133 (Diskussion) 22:46, 27. Jul 2011 (CEST))
Konturplot oder Beschriftung falsch
Diese Abbildung kann nicht (quantitativ) korrekt sein: L1 und L2 sind viel zu weit von der Erde entfernt, verglichen mit dem Abstand der Erde zur Sonne. Statt 1% (1,5 Mio. km aus dem Artikel zu Erdbahnradius) messe ich 30% am Bildschirm. Wenn für den Planeten eine viel größere Masse genommen wurde, damit man das Wesentliche erkennen kann, schön, aber dann darf man eben nicht dazuschreiben, dass es sich um die Erde handelt. Auf der Bildbeschreibungsseite und der Herkunftsseite wird auch von der Erde gesprochen (teilweise impliziert), aber nicht, ob es sich um mehr als eine Veranschaulichung handelt. --Mopskatze℅Miau! 21:34, 31. Jul. 2011 (CEST) P.S.: Letztere gibt doch an: (not drawn to scale!)., daher ist es nur eine Veranschaulichung.
Dreidimensionalität als "Lagrange-Ring"?
Bei der Darstellung von L1, L2 und L3 ist klar, das diese in der Achse Hauptgestirn-Planet stehen - und sind damit theoretisch "in eindimensionaler Konstellation". L4 und L5 sind jedoch nicht mehr auf einer einzigen Linie anzuordnen - und dann wird eben in die Bahnebene erweitert. Nun stelle ich die Frage, ob das wirklich nur zwei Punkte sein müssen - oder ob das nicht vielmehr ein ganzer, mit dem Planet "mitwandernder", Ring sein müsste, auf dem natürlich L4 und L5 die jeweils äusseren Punkte sind - also rotationssymmetrisch um die Achse Hauptgestirn-Planet als Ring- (relativ) resp. Spiral- (absolut) -bahn mit L4 und L5? --ProloSozz 12:43, 9. Aug. 2011 (CEST)
- Ohne es im Detail durchgedacht zu haben: Nein. Nehmen wir karthesische Koordinaten an (mitdrehend oder nicht ist erstmal egal), die Verbindungsachse wäre x, die zweite in der Bahnebene y und die senkrecht dazu z. Sobald der "Sattelit" eine Position mit z ungleich Null einnimmt, wirken die Kräfte der "Sonne" und die des "Planeten" Richtung z=0. Diese kann aber im Gegensatz zu y ungleich Null nicht durch die Zentrifugalkraft ausgeglichen werden (Kreisbewegung nur in x-y-Richtung), weswegen kein Gleichgewicht möglich ist. Das Einzige was ich mir vorstellen könnte wäre eine Oszillation um z=0, wobei ich stark davon ausgehe dass sowas in x-y-Richtung dann nicht mehr periodisch funktioniert. --Schweizerfranke (Diskussion) 23:03, 12. Jul. 2012 (CEST)
Der Mond und die Lagrange-Punkte
Der Mond kreist zur Zeit in einem Abstand von ungefähr 384.000 km um die Erde. Er entfernt sich dabei derzeit um einige Zentimeter pro Jahr von der Erde.
Die Lagrange-Punkte L1 und L2 liegen laut diesem Artikel etwa 1,5 Mio. km innerhalb bzw. außerhalb der Erdumlaufbahn um die Sonne. Die Lagrange-Punkte L4 und L5 befinden sich laut diesem Artikel gemäß einem gleichseitigen Dreick 60 Grad vor bzw. hinter der Erde auf der gleichen Umlaufbahn. Daher laufen diese Punkte mit einem Abstand von 1 AE oder etwa 150 Mio. km auf der gleichen Umlaufbahn vor bzw. hinter der Erde mit.
Da sich der Mond von der Erde entfernt, wird er irgendwann (in einigen Mio. Jahren) den Bereich der Punkte L1 oder L2 erreichen. Irgenwann später (in einigen hundert Mio. Jahren) wird der Mond den Bereich der Punkte L4 oder L5 erreichen. Was passiert dann?
Wird der Mond z. B. in L1 oder L2 "hängen bleiben"? Oder entfernt er sich weiter von der Erde? Nur, um dann vielleicht in L4 oder L5 "hängen zu bleiben"? Denn das sind ja stabile Lagrange-Punkte, im Gegensatz zu den erstgenannten.
Also, in L4 oder L5 ist der Mond weiter entfernt, als heute die Venus (im günstigsten Fall) und damit ein Lichtpunkt weit dunkler als diese.
Aber wie sieht es mit L1 und L2 aus? Der Mond ist dann etwa 4 mal weiter entfernt, als heute und damit 4 mal kleiner. "Eiert" er dann um diese Punkte? Schließlich sind die nicht stabil. Ein "normaler" Mond-Monat dürfte dabei nicht herauskommen. Ist zwar nur eine hypothetische Frage, weil wir (ich) das sowieso nicht erleben werden, aber mich interressieren andere Meinungen dazu.
--Ch.Weg (Diskussion) 23:58, 18. Dez. 2012 (CET)
- Hallo Ch.Weg! Du schreibst "Da sich der Mond von der Erde entfernt, wird er irgendwann (in einigen Mio. Jahren) den Bereich der Punkte L1 oder L2 erreichen". Nein, wird er nicht. Die Lage L-Punkte hängt ja von der Mondposition ab. Wenn sich der Abstand Erde-Mond verändert, verändern auch die L-Punkte ihre Lage. L2 liegt immer hinter dem Mond, auch wenn sich der Abstand Erde-Mond vergrößert. Der Mond kann nie zu L2 gelangen. --Asdert (Diskussion) 11:20, 19. Dez. 2012 (CET)
- Pardon, das muss ich präzisieren. Die Lage von L1 und L2 hängt vom Massenverhältnis von Sonne und Erde (noch genauer: von Erde und Mond zusammen) ab und wird sich daher nur sehr wenig verschieben. Abgesehen davon wird die Vergrößerung der Mondbahn zum Stillstand kommen, wenn der Drehimpuls der Erde auf die Mondbahn übergegangen ist (die Erde wird dann dem Mond immer die gleiche Seite zukehren, so wie der Mond der Erde jetzt schon). Auch bei einer konstanten Vergrößerung würde es Dutzende von Mia Jahren dauern, bis der Mond L1/L2 erreicht, er würde aufgrund seines Drehimpulses aber auch dann nicht "hängenbleiben". Allerdings wäre ein so weit außen befindlicher Mond sehr anfällig für Störungen und könnte leicht von einem vagabundierenden Körper "gestohlen" oder sonstwohin ins Sonnensystem katapultiert werden. --Raumfahrtingenieur (Diskussion) 12:07, 19. Dez. 2012 (CET)
- @ Asdert! Da möchte ich widersprechen. Die Lagrange-Punkte sind ja - hmm, ich als Laie nenne das mal: "schwerkraftstabile Punkte innerhalb eines Systems von 2 bewegten Himmelskörpern". Und dabei ist hier das System Sonne - Erde gemeint. Der Mond ist zwar in dieses System eingebunden, das System hängt aber nicht von diesem ab, sondern beeinflußt ihn höchstens. Daher ist es durchaus denkbar, daß der Mond irgendwann einmal den Bereich der L-Punkte erreicht. Wohlgemerkt: ich sprach von vornherein von dem Bereich der Lagrange-Punkte. Gemeint ist natürlich der Bereich, in dem diese heute liegen. Von einem Bereich oder Ort, an dem diese Punkte in einer möglichen fernen Zukunft liegen können, habe ich nichts geschrieben.
- @ Raumfahringenieur! Klar hängt die Entfernung des Mondes von der Erde auch mit dem Drehimpuls der Erde zusammen. Oder mit den Drehimulsen zwischen der Erde und dem System Erde - Mond. Aber, endet diese Vergrößerung der Mondumlaufbahn wirklich, bloß weil die Erde dann an einem weit entfernten Zeitpunkt eine gebundene Rotation zum Mond aufweist? Oder entfernt sich der Mond trotzdem weiter von der Erde? Falls ja, natürlich weiterhin auf Kosten der Rotation der Erde, die sich dann ggf. irgendwann an die Sonne bindet? Schließlich ist das Ganze eine Interaktion zwischen verschiedenen Masseobjekten. Und dem Mond fällt bestimmt nicht irgendwann ein: "Jawoll, ich habe mein Ziel erreicht; ich bleibe jetzt auf dieser Umlaufbahn."
- Natürlich wird die Mondbahn störanfälliger, je weiter außen sich der Mond befindet. Du sprachst von den Lagrange-Punkten L1/L2. Diese liegen derzeit bei einer Erdentfernung von etwa 1,5 Mio. km, also ungefähr der 4-fachen Mondentfernung oder 1/100 AE. Macht das wirklich schon soviel aus, daß der Mond der Erde von einem anderen Planeten "gestohlen" werden könnte?
- Zum Erreichen der Punkte L1/L2 bzw. L4/L5 sprach ich von mehreren Mio. bzw. mehreren 100 Mio. Jahren. Du hast mehrere Mrd. Jahre entgegengesetzt. Ich hab's - ehrlich gesagt - nicht ausgerechnet, sondern einfach mal "Pi mal Daumen" postuliert.
--Ch.Weg (Diskussion) 02:34, 21. Dez. 2012 (CET)
- Für die Zeitdauer habe ich etwas naiv 1,1 Mio km durch 3 cm/Jahr geteilt und komme dann auf 36 Mia Jahre. Die Vergrößerung der Mondbahn geschieht allerdings durch die Gezeitenreibung, die Drehimpuls von der Erdrotation auf die Mondbahn überträgt. Ist eine gegenseitig gebundene Rotation erreicht, kommt dieser Austausch zum Erliegen. Der "finale Radius" der Mondbahn lässt sich daher gut abschätzen, für eine genaue Rechnung muss man aber die in der Tiefe ungleichmäßige Massenverteilung der Erde (kleineres I als eine homogene Kugel) berücksichtigen. Störungen durch äußere Körper können - vor allem im Fall von Resonanzen - durchaus auch für Körper, die sehr viel weiter innen liegen als L1/L2, eine Rolle spielen; erheblich wahrscheinlicher als die "Aneignung" durch einen anderen Körper ist allerdings, dass der Mond durch eine solche Störung auf eine Sonnenumlaufbahn gerät. --Raumfahrtingenieur (Diskussion) 09:08, 21. Dez. 2012 (CET)
Ok. Etwa 36 Mrd. Jahre, bis der Mond sich so weit entfernt hat, daß er L1/2 erreicht. Das ist natürlich lange nach "Nova Solis", oder wie auch immer wir den Zeitpunkt nennen wollen, an dem sich die Sonne - wenn schon nicht zur Nova - dann aber wenigstens zum Roten Riesen ausdehnen wird. Wenn durch diese Ereignisse die Erde nicht durch die Sonne "geschluckt" werden sollte, dürften sich die Schwerkraftverhältnisse wohl derart ändern, daß sich weitere Berechnungen zum Monsbahnradius erst einmal erübrigen.
--Ch.Weg (Diskussion) 00:34, 23. Dez. 2012 (CET)
"An diesen Punkten im Weltraum heben die Schwerkräfte ZWEIER benachbarter Himmelskörper und die Zentrifugalkraft der Bewegung einander auf, so dass jeder der DREI Körper kräftefrei ist"
=> Um wieviele Körper geht es denn nun? (nicht signierter Beitrag von Sundancerl (Diskussion | Beiträge) 12:21, 10. Apr. 2013 (CEST))
- "die Schwerkräfte ZWEIER benachbarter Himmelskörper" auf einen dritten mit vernachlässigbar kleiner Masse. Die beiden ersten umkreisen einander und sind daher im rotierenden Bezugssystem, das hier eingesetzt wird, eh kräftefrei. Der zitierte Satz ist aber schon etwas unglücklich formuliert. --Hob (Diskussion) 13:22, 10. Apr. 2013 (CEST)
librare
"vom lateinischen librare für „schwanken“ oder „das Gleichgewicht halten“)"; ich will nicht korinthenkacken, aber meinereiner meint, dass "schwanken" und "das Gleichgewicht halten" sich ausschließen, also geradezu Antonyme sind; imho bedeutet das nur letzteres, oder eben "die Waage halten", was sich die Waage (libra) "hält", schwankt eben gerade nicht nicht. Oder? --Janneman (Diskussion) 15:18, 10. Apr. 2013 (CEST)
- Na ja, wenn ich mir eine Balkenwaage vorstelle, die nicht im Gleichgewicht ist, sehe ich, dass sie sich einmalig zur schwereren Seite neigt. Wenn sie im Gleichgewicht ist, schwankt der Waagebalken hin und her, bis er irgendwann (bei guten und ungedämpften Waagen ziemlich spät) zur Ruhe kommt. Mit etwas Erfahrung kann man am Zeiger sehen, ob dieser symmetrisch zur Mittellage ausgelenkt wird. Also kein Antonym. --Slartibartfass (Diskussion) 15:29, 10. Apr. 2013 (CEST)
- eben, "zur Ruhe kommt". Zugegebenermaßen verstehe ich von Physik wenig bis nix, aber ist es nicht vielmehr so, dass das Gleichgewicht sich erst einstellt, wenn das Schwanken des Waagebalkens aufhört? --Janneman (Diskussion) 16:00, 10. Apr. 2013 (CEST)
Graphik zur Stabilität der Lagrange-Punkte
Stehe ich völlig auf der Leitung, aber wenn ich (für mich naheliegenderweise) davon ausgehe, dass die Bereiche innerhalb der blauen Pfeile stabile Bereiche kennzeichnen und jene der roten eben instabile, sollten dann die Farben der Pfeile von L1 bis L3 nicht vertauscht werden??? Und falls sich da schon jemand darüber hermacht, wärs für mich auch logischer, die Pfeile für L4 und L5 zu wenden, sodass die Richtung der Spitzen den stabilen Bereich umreißen. Schlußendlich sollte es jedenfalls einheitlich sein. --WFL65 (Diskussion) 16:24, 10. Apr. 2013 (CEST)
- Was zur Unverständlichkeit der Grafik beiträgt, ist, dass die Pfeile keine richtigen Pfeile, sondern gleichseitige Dreiecke sind. Wenn man nicht von vornherein weiß, wohin ein Pfeil zeigt, hat man bei jedem die Auswahl zwischen drei Möglichkeiten. Dazu kommt, dass die beiden Rudel von blauen Pfeilen, die die stabilen Punkte L4 und L5 umgeben, nicht jeweils auf einer Konturlinie liegen.
- Naja, so streng sehe ich es nicht, der Text ist ja soweit verständlich und so kann ich für ein nierenförmiges Feld auch bei gleichlangen Seiten eine Basis und eine Spitze sehen (für L4/L5 ist die Basis innerhalb des stabilen Bereiches, die Spitzen zeigen nach außen), und da ich die Fläche eher symbolisch sehe, stoße ich mich auch an keiner fehlenden Konturlinie. Allerdings bin ich wegen der Farben für L4/L5 davon ausgegangen, dass auch bei L1-3 die blauen Pfeile die stabilen Positionen kennzeichnen, was mich aufgrund des gelesenen Textes doch verwirrt hatte. Also Text nochmals gelesen, ja, und auch beim zweiten Lesen so verstanden, dass dort die roten Pfeile die stabilien Bereiche markieren sollten. Und dann zeigen für mein Verständnis dort die Pfeile plötzlich in die Gegenrichtung. Also auf Hoffnung auf Aufklärung oder Korrektur den Beitrag hier verfasst.
- P.S. Ach ja, bitte mit MinusMinusTildeTildeTildeTilde signieren, danke --WFL65 (Diskussion) 19:17, 10. Apr. 2013 (CEST)
- Das Problem ist (und ich bin auch über diese Stabilitäts-Frage gestolpert ^^), dass die Graphik offenbar aus der englischen wikipedia übernommen wurde, aber nicht die Bildunterschrift:
- "A contour plot of the effective potential due to gravity and the centrifugal force of a two-body system in a rotating frame of reference. The arrows indicate the gradients of the potential around the five Lagrange points — downhill toward them (red) or away from them (blue). Counterintuitively, the L4 and L5 points are the high points of the potential. At the points themselves these forces are balanced."
- Eigentlich ist mit der dreidimensionalen Grafik alles viel klarer... da muss man keine Pfeile einzeichnen, sondern "sieht" in welche Richtungen es auf- und abwärtsgeht.
- Was ich mich noch frage: Wenn man die Corioliskraft ignoriert, sind ja alle Punkte instabile Gleichgewichtspunkte - die Sattelpunkte sowieso und die lokalen Maxima auch. Was passiert jetzt also mit dem leichtesten Körper, wenn das Massenverhältnis der anderen beiden kleiner als 24.96 ist? Lenkt ihn die Corioliskraft nicht genug ab und er trudelt langsam *spiralförmig* ins "Verderben" (sprich in die Weite des Alls hinaus bzw. in die Wonne der Hitze der Sonne bzw. den harten Aufschlag auf den Planeten)? Hängt die Corioliskraft nicht auch noch von und nicht nur von m ab?
- Und: Was um Himmelsmechaniks Willen soll eine "nierenförmige Bahn" sein? --Red*Star (Diskussion) 09:30, 30. Mai 2013 (CEST)
- edit: Hab die Bildunterschrift mal korrigiert. Eine dritte Frage fällt mir gerade auch noch ein: Ist die Corioliskraft auch dafür verantwortlich, dass Sonden die Lagrange-Punkte "umkreisen" können (anderenfalls müssten sie ja ziemliche Mengen an Treibstoff mitführen)? Wenn das stimmt, könnte man das vielleicht noch in den Artikel mit aufnehmen. --Red*Star (Diskussion) 10:05, 30. Mai 2013 (CEST)
Wird der Lagrange-Punkt umkreist?
Beim Lagrange-Punkt L1 steht im Beispiel: Schon 1978 brach dorthin die Sonde ISEE-3 auf, um ihn bis 1982 zu umkreisen. Sie war die erste Sonde, die einen Lagrangepunkt umkreiste. Ich habe aber die Sache so verstanden, dass nur der Lagrange-Punkt selbst eine stabile Lage darstellt und nicht eine für mich nicht nachvollziehbare Umlaufbahn darum. --Nikstukas (Diskussion) 17:53, 28. Okt. 2013 (CET)
- Raumsonden können mit relativ wenig Korrekturmanövern in der Nähe der L-Punkte bleiben. Siehe Lagrange-Punkte#Stabilität der Lagrange-Punkte und Halo-Orbit. --Asdert (Diskussion) 19:59, 28. Okt. 2013 (CET)
- Falls es nur um das In-der-Nähe-Bleiben geht, sind gar keine Manöver nötig. 'Umkreisen' trifft die Bewegungsform eher schlecht, meist ist es eher ein 'Umwickeln'. – Rainald62 (Diskussion) 22:06, 28. Okt. 2013 (CET)
Mathematik zum Artikel
Es wäre toll, wenn dieser Artikel etwas mehr Mathematik enthielte. Insbesondere folgendes:
- Herleitung der Formeln für die Lage aller fünf Punkte.
- aufzeigen, warum der Winkel von L4/L5 immer 60° beträgt
- Herleiten, warum L4 und L5 stabile Gleichgewichte sind (Keine Angst vor den Ableitungen einer Funktion).
- Ein paar Grafiken zu den geschrieben Worten wären gut.
Ggf. kann man die oben gelisteten Formeln mitnutzen. ÅñŧóñŜûŝî (Ð) 15:54, 16. Nov. 2010 (CET)
- ich schließe mich an, Lagrange-Punkte L1 bis L3: Sie lassen sich rechnerisch herleiten, ist ja eine tolle Ankündigung und dann folgt: NICHTS. Soweit ich es gerechnet habe, gelangt man zu einer Gleichung 5.Ordnung, die sich nicht rechnerisch lösen läßt. Die Ausgangsgleichung lautet: G*M/L² = G*m/l² + ome²(L-r*M/(m+M)) mit L=Abstand zu M und l=Abstand zu m. Edit: korrigiert und die Gleichung lautet dann vereinfacht: s/L²=(1-s)/(1-L)² + (L-1+s) mit L*r = Abstand L1 zu M und s*r=Abstand m zum Drehzentrum. Ra-raisch (Diskussion) 19:15, 29. Jan. 2015 (CET)
Unter Einführung einer Größe für die Exzentrizität des gemeinsamen Schwerpunktes e=|SH|/r und der Exzentrizität des L1-Punktes d=|LH|/r erhält man folgende Formel e(d)=-d(1+(0.5²-d²)²) / ((0.5²-d²)² -(1+4d²)0.5), mit der man aus einem gegebenen L1-Punkt den Schwerpunkt des Systems berechnen kann, aber eben nicht umgekehrt.
Ra-raisch (Diskussion) 11:16, 7. Jan. 2015 (CET)
- ich habe vorhin die Lösung von Roche-Grenze eingefügt Ra-raisch (Diskussion) 21:32, 28. Jan. 2015 (CET)
- ich habe in einer Publikation folgende Formeln mit Ansatz aber ohne weiteren Rechenweg gefunden: L1=1-(M/(m+M))^(1/3), L2=1+(M/(M+m))^(1/3), L3=-(1+5M/(12(M+m))), aber alle außer meiner Formel ergeben für M=m einen von r/2 abweichenden L1, das kann also nicht richtig sein, wenn er von 0,5 verschieden wäre, gäbe es ja zwei Punkte, beide Massen M und m sind ja dann "gleichberechtigt". Ra-raisch (Diskussion) 18:23, 29. Jan. 2015 (CET)
- Mist, jetzt hab ichs verstanden, im Artikel der Roche-Grenze wurde ja die Zentrifugalkraft bei der Formel außer Acht gelassen....immerhin ist meine Formel zur Rückrechnung exakt Ra-raisch (Diskussion) 18:51, 29. Jan. 2015 (CET)
- endlich ist es mir gelungen, die gefunde Formel zu vergleichen, es war etwas schwierig, sie ins gleiche Format umzuformen (Spiegelung, Nullpunkt, Drehung, Skala...). Ich füge den Vergleichsgraf bei, zwar nur für L1 aber gehe davon aus, dass es dann schon für L2 und L3 auch stimmt. Grafik füge ich gleich noch bei ...hochgeladen und doch noch geschafft Ra-raisch (Diskussion) 21:51, 29. Jan. 2015 (CET)
- In der aktuellen Form sind die Gleichungen im Artikel unbrauchbar. Was ist r, und wie kann ein Punkt (linke Seite) gleich einer Länge (rechte Seite) sein? --mfb (Diskussion) 20:36, 30. Jan. 2015 (CET)
- Ich nehme an, dass Dir die Antwort auf die Frage selbst bewusst war, ich habe es nun beschriftet und angepasst. Ra-raisch (Diskussion) 23:23, 14. Feb. 2015 (CET)
- Nein, ich hatte nur nicht mehr an den Artikel gedacht. Die aktuellen Formeln können nicht passen. Nehmen wir Erde/Sonne mit einem Massenverhältnis von M=1000000m, also µ≈2. Dann wäre und somit ziemlich nah an der Sonne. Sollte das vielleicht "m" im Zähler sein bei der Definition von µ? Dann sieht der Wert gut aus. --mfb (Diskussion) 02:30, 15. Feb. 2015 (CET)
- oha da habe ich mich tatsächlich beim Abschreiben vertippt danke vielmals Ra-raisch (Diskussion) 01:20, 17. Feb. 2015 (CET)
- Nein, ich hatte nur nicht mehr an den Artikel gedacht. Die aktuellen Formeln können nicht passen. Nehmen wir Erde/Sonne mit einem Massenverhältnis von M=1000000m, also µ≈2. Dann wäre und somit ziemlich nah an der Sonne. Sollte das vielleicht "m" im Zähler sein bei der Definition von µ? Dann sieht der Wert gut aus. --mfb (Diskussion) 02:30, 15. Feb. 2015 (CET)
- Ich nehme an, dass Dir die Antwort auf die Frage selbst bewusst war, ich habe es nun beschriftet und angepasst. Ra-raisch (Diskussion) 23:23, 14. Feb. 2015 (CET)
- In der aktuellen Form sind die Gleichungen im Artikel unbrauchbar. Was ist r, und wie kann ein Punkt (linke Seite) gleich einer Länge (rechte Seite) sein? --mfb (Diskussion) 20:36, 30. Jan. 2015 (CET)
ich bin mir nicht sicher, ob diese beiden Punkte exakt oder genähert sind, und wie man das mit der seitlichen Koordinate formulieren sollte:
Ra-raisch (Diskussion) 01:39, 17. Feb. 2015 (CET)
„Umkreisen“ der Lagrange-Punkte?
Warum „umkreisen“ künstliche Satelliten die Lagrange-Punkte, wie es mehrfach im Artikel heißt? In der Einführung wird doch gesagt, dass Forschungssatelliten dort kräftefrei ruhen können. Zwar sind die Punkte nicht komplett stabil, aber kleinere Lagekorrekturen der Satelliten sollten doch ausreichen, sie dort zu halten. Was habe ich hier nicht verstanden? --Till.niermann (Diskussion) 20:40, 29. Apr. 2015 (CEST)
- Zum Einen ist der Punkt nicht so ganz exakt - die Erde macht keine Kreisbahn, der Mond stört und so weiter, man ist also immer nur irgendwo in der Nähe eines (hypothetischen) Punktes, und den zu umkreisen ist einfacher. Zum Anderen sollen die Satelliten gegenseitig Abstand halten. Beim L2 kommt dazu, dass man in der Regel den Erdschatten vermeiden will - schlecht für Solarzellen, für thermische Belastungen und so weiter. --mfb (Diskussion) 23:26, 29. Apr. 2015 (CEST)
Angaben zu den Lagrange-Punkten
Ich schlage vor, die folgenden Angaben zu den Lagrange-Punkten L1 und L2 von Erde und Mond in den Artikel einzufügen, weil diese Lagrange-Punkte der Erde nahe liegen:
Der innere Lagrange-Punkt L1 von Erde und Mond ist im Mittel ungefähr 58000 Kilometer vom Massemittelpunkt des Mondes in der Richtung zur Erde hin entfernt.[1]
Der äußere Lagrange-Punkt L2 von Erde und Mond ist im Mittel ungefähr 64500 Kilometer vom Massemittelpunkt des Mondes in der Richtung von der Erde weg entfernt.[1]
- ↑ a b Jerome Pearson, Eugene Levin, John Oldson, and Harry Wykes: The Lunar Space Elevator (PDF; 365 kB), STAR Inc., Mount Pleasant, SC USA, 55th International Astronautical Congress, Vancouver, Canada, 4-8 October 2004.
-- Karl Bednarik (Diskussion) 14:38, 14. Aug. 2015 (CEST).
Hallo Rainald62, die Angaben zu den Lagrange-Punkten von Erde und Mond sind zwar modellabhängig, aber die Unterschiede zwischen den verschiedenen Angaben sind nicht besonders groß. Wie groß wäre denn der maximale Unterschied? Der Bedarf, gerade für das Erde-Mond-System Angaben zu machen, besteht darin, dass es sich um die der Erde am nächsten liegenden Lagrange-Punkte handelt. Außerdem wurden L1 und L2 von Erde und Mond bereits raumfahrttechnisch genutzt. -- Karl Bednarik (Diskussion) 07:56, 17. Aug. 2015 (CEST).
- Die Frage kann ich dir nur mit einer Schätzung beantworten – Größenordnung 1 Prozent. Dass seriöse Angaben schwer zu finden sind, ist ein Zeichen für die geringe Relevanz. Nach "genutzt" hatte ich gesucht und nichts gefunden. Falls es zutrifft, mag die Angabe in den Artikel, zusammen mit dem Modell, allerdings unter Beispiele. --Rainald62 (Diskussion) 08:37, 17. Aug. 2015 (CEST)
- Hallo Rainald62, es handelt sich dabei um die ARTEMIS-Missionen:
- http://www.igpp.ucla.edu/public/THEMIS/SCI/Pubs/artemis/artemis_woodward.pdf
- http://www.nasa.gov/mission_pages/themis/news/artemis-orbit.html
- Berechnungen und Ergebnisse:
- http://www.merlyn.demon.co.uk/gravity4.htm#NaN
- Mit freundlichen Grüßen, -- Karl Bednarik (Diskussion) 08:42, 18. Aug. 2015 (CEST).
L4 und L5
In das Artikel : "Diese beiden Lagrange-Punkte befinden sich (annähernd) jeweils am dritten Punkt eines gleichseitigen Dreiecks, dessen Grundlinie die Verbindungslinie der beiden großen Körper ist. L4 befindet sich in Umlaufrichtung des kleineren der beiden großen Körper vor ihm, L5 hinter ihm. Der L4- und L5-Punkt liegen also 60° vor beziehungsweise 60° hinter dem um den Zentralkörper umlaufenden Körper in seiner Umlaufbahn." Nicht "annähernd" : das Dreieck zwischen den Zentren der drei Massen genau gleichseitig ist. Aber nicht "in seiner Umlaufbahn" : nur annähernd so. Bitte lesen Sie http://www.merlyn.demon.co.uk/gravity4.htm, auch 5 & 6. 94.30.84.71 23:19, 28. Mär. 2012 (CEST)
- Danke für den Hinweis (ist im Text längst repariert) und für die Quelle (daraus könnte noch mehr eingearbeitet werden). --Rainald62 (Diskussion) 23:26, 1. Sep. 2015 (CEST)
Bilder
Warum ist die Lage der Punkte L4 und L5 in den verschiedenen Bildern unterschiedlich dargestellt? In Bild 1 und 2 liegen sie eindeutig auf der Umlaufbahn des kleineren Himmelskörpers, bei Bild 3 kann man bei genauer Betrachtung herauslesen, daß sie etwas außerhalb dieser Bahn liegen, und bei Bild 6 schließlich liegen sie deutlich außerhalb der Bahn des kleineren Körpers. Letztere Darstellung ist meiner Ansicht nach richtig (natürlich nicht maßstäblich). --Tscheini (Diskussion) 23:29, 31. Aug. 2015 (CEST)
- Hängt davon ab, ob man in das Koordinatensystem der Sonne geht oder den Schwerpunkt des Planet/Sonne-Systems nimmt. --mfb (Diskussion) 00:54, 1. Sep. 2015 (CEST)
- Bei meiner Aussage bin ich vom Idealfall ausgegangen, d.h. der Schwerpunkt des Planeten läuft auf einer Kreisbahn, andere Himmelskörper haben keinen Einfluß und das ganze System dreht sich um den Schwerpunkt des Planet-Sonne-Systems. Vom Sonnen-Schwerpunkt sind Planet und L4 (oder L5) gleich weit entfernt (gleichseitiges Dreieck). Der System-Schwerpunkt ist je nach Massenverhältnis vom Sonnen-Schwerpunkt in Richtung Planet verschoben, dessen Bahnradius ist also kleiner als die Seitenlänge des Dreiecks. Auch der Abstand der Punkte L4 / L5 vom System-Schwerpunkt ist kleiner als die Seitenlänge des Dreiecks, aber die Verkürzung ist wegen der anderen Richtung geringer als beim Planeten. Nimmt man den Extremfall, daß die Massen von Sonne und Planet gleich groß sind, dann liegt der System-Schwerpunkt auf halbem Wege zwischen Sonne und Planet, der Bahnradius entspricht also bei beiden der halben Seitenlänge des Dreiecks. Der Abstand der Punkte L4 / L5 vom System-Schwerpunkt ist dagegen um den Faktor größer als der des Planeten.--Tscheini (Diskussion) 17:14, 1. Sep. 2015 (CEST)
- Das ist richtig. Der Abbildung 1 kann man zubilligen, dass das Massenverhältnis größer ist als in den Abbildungen 2, 3 und 6, sodass die Abweichung gering ist. Grob falsch ist also nur Bild 2. Es hat auch keinen Mehrwert gegenüber 3 und 6. Ich nehme es raus. --Rainald62 (Diskussion) 23:26, 1. Sep. 2015 (CEST)
darstellungstheoretische Ergänzung?
Einen ergänzenden Hinweis, der – vielleicht Galois erwähnend – knapp erläutert, warum eine allgemeine polynomiale Gleichung von höherem Grad als 4 im Allgemeinen nicht durch Radikale aufgelöst werden kann, deshalb i. A. eine exakte algebraische Lösung nicht möglich ist – und man daher auf numerische Verfahren angewiesen sein kann –, finde ich in diesem Artikel nicht; ich fände den jedoch hier ziemlich passend und vermisse ihn insofern. --nanu *diskuss 21:54, 5. Dez. 2015 (CET)
- Hallo nanu! Ich würde so einen Hinweis eher unpassend finden, weil es ganz irrelevant ist, ob die Lösungen durch Radikale angebbar sind oder nicht: In beiden Fällen wird man in der Praxis zu rationalen Näherungswerten greifen und solche findet man bei Vorliegen einer exakten (algebraisch dargestellten) Lösung wohl kaum leichter als ohne so ein Zwischenresultat. Die höhergradige Gleichung läßt sich ja auch durch direkte Methoden rasch und zuverlässig näherungsweise lösen. Liebe Grüße, Franz 23:45, 5. Dez. 2015 (CET)
Einleitung einfacher
Ich vermisse im Artikel vor allem eines: eine einfachere Antwort auf die Frage „was ist das?“ ganz am Anfang. Die vorliegende Einleitung steigt mit numerischen und analytischen Lösungen sowie Nullstellen gleich sehr wissenschaftlich ein. Für einen nicht physikalisch-mathematisch vorgebildeten Leser wäre der Artikel viel nützlicher, wenn man eine gnadenlos laienverständliche Erklärung vorausschickt und erst danach exakter wird.
Vorschlag:
Die Lagrange-Punkte oder Librationspunkte (von lateinisch librare „das Gleichgewicht halten“) sind die Gleichgewichtspunkte des eingeschränkten Dreikörperproblems. In diesen fünf Punkten eines Systems zweier massereicher Körper, etwa eines Planeten und seines Zentralgestirns, befinden sich alle auf einen dritten, viel leichteren Körper wirkenden Kräfte im Gleichgewicht. Das bedeutet, dass der leichte Körper in einem der Lagrange-Punkte eine stabile Umlaufbahn mit der Umlaufzeit des Planeten beschreiben kann, ohne dass es zu Störungen von seiten eines der beiden anderen Körper kommt.
Das allgemeine Dreikörperproblem der Himmelsmechanik ist nur numerisch lösbar … [weiter wie vorliegend].
Wie fändet ihr das? --Kreuzschnabel 17:41, 13. Jul. 2016 (CEST)
- Ich stimme Dir zu. Einziger Einwand: das Wort "stabil" halte ich für fragwürdig, siehe Lagrange-Punkte#Stabilität der Lagrange-Punkte. --Asdert (Diskussion) 12:36, 17. Jul. 2016 (CEST)
Ja, bitte unbedingt vereinfachen, das ist völlig überhöhtes fachchinesisch am Anfang, eine einfache Einleitung gehört m.E. zu einem lesenswerten Artikel einfach dazu, egal wie toll er später sein mag. Ich finde den Vorschlag einen sehr guten Anfang, möge ein Fachkundiger ihn endgültig abnicken. --Thhart (Diskussion) 11:18, 15. Sep. 2016 (CEST)
- Guter Vorschlag. Mit dem "stabil" habe ich auch Probleme. Und was sagt der letzte Satz? Störungen sind es ja nicht, beide Systeme werden bereits berücksichtigt bei der Definition. Wird der Orbit der Erde durch die Sonne gestört? --mfb (Diskussion) 20:53, 15. Sep. 2016 (CEST)
Ich möchte auch den Begriff des eingeschränkten Dreikörperproblems noch weiter nach hinten nehmen. IMHO muß eine Einleitung auch ohne Vorbildung verständlich sein, ohne einzelne Termini extra nachschlagen zu müssen und möglicherweise den Leser in eine Nachschlage-Kaskade zu schicken, bevor der erste Satz auch nur zu Ende gelesen ist. Da nehme ich lieber leichte Ungenauigkeiten oder unscharfe Formulierungen in Kauf und bevorzuge beispielhafte, wenn auch zu spezielle Aussagen gegenüber umfassenden, aber abstrakten.
Nächster Vorschlag, noch etwas konkreter und ent-fachchinesischt:
Die Lagrange-Punkte oder Librationspunkte (von lateinisch librare „das Gleichgewicht halten“) sind fünf Punkte im System zweier Himmelskörper (beispielsweise eines Planeten und des von ihm umkreisten Sterns), an denen sich alle von den beiden Körpern beziehungsweise ihren Umlaufbahnen erzeugten Schwer- und Fliehkräfte aufheben. Ein leichter Körper (etwa ein Satellit) kann an einem der Lagrange-Punkte antriebslos den Stern mit derselben Umlaufzeit wie der Planet umkreisen, wobei sich seine Position relativ zum Planeten nicht ändert.
Mathematisch betrachtet sind die Lagrange-Punkte die Gleichgewichtspunkte des eingeschränkten Dreikörperproblems. Das allgemeine Dreikörperproblem der Himmelsmechanik ist nur numerisch lösbar … [weiter wie vorliegend].
--Kreuzschnabel 10:46, 17. Sep. 2016 (CEST)
Hab’s jetzt mal so eingesetzt. Danke fürs Mitdenken! --Kreuzschnabel 13:20, 26. Sep. 2016 (CEST)
L2 - Teleskope Herschel und Planck
Im Abschnitt L2 wird noch darüber gesprochen dass die beiden Teleskope auf dem Weg seien, allerdings sind sie mittlerweile positioniert. Herschel ist seit dem 14.7.2009 in Betrieb. http://www.esa.int/SPECIALS/Herschel/SEM76A0P0WF_0.html Auch Planck ist wohl angekommen, allerdings habe ich nicht herausgefunden, wann es in Betrieb genommen wurde/wird. Laut diesem Artikel irgendwann Mitte August. http://www.esa.int/SPECIALS/Planck/SEM0Y5S7NWF_0.html
-- 80.156.44.33 17:00, 31. Jul. 2009 (CEST)
Siehe auch
Die Begriffe hängen in der Luft. Kann jemand den bezug formulieren? (WP:SA) --Siehe-auch-Löscher (Diskussion) 13:04, 10. Apr. 2013 (CEST)
Konstanz der Orte
?? Imho rücken z.B. L1 und L2 mit steigendem Massenverhältnis zusammen. -- Rainald62 (Diskussion) 00:47, 5. Aug. 2013 (CEST)
"Satelliten"?
Mich verwirrt, dass häufig (und auch in diesem Artikel!) Sonden, die sich an Lagrange-Punkten der Erde befinden, "Satelliten" genannt werden. Sie sind aber doch keine Satelliten (siehe Satellit (Raumfahrt)), weil sie die Erde nicht umkreisen. --Neitram ✉ 11:03, 30. Okt. 2017 (CET)
- Stimmt, der Ausdruck ist da falsch. Ich habe es in "Raumsonde" geändert. Danke für den Hinweis. --Asdert (Diskussion) 11:23, 30. Okt. 2017 (CET)
- Alle fünf Lagrange-Punkte des Erde-Mond-Systems umkreisen die Erde, bezogen auf das nicht rotierende Universum. Die fünf Lagrange-Punkte des Erde-Mond-Systems ruhen nur in einem mit dem Mond mit rotierenden Bezugssystem. Bei den fünf Lagrange-Punkten des Sonne-Erde-Systems handelt es sich daher dann um Satelliten der Sonne. -- Karl Bednarik (Diskussion) 11:35, 30. Okt. 2017 (CET).
- Ich hatte die Lagrange-Punkte des Sonne-Erde-Systems gemeint. Du hast Recht, diese Sonden umkreisen in der Tat die Sonne und dies ist vom Begriff "Satellit" auch mit abgedeckt -- was ich zuvor nicht bewusst auf dem Schirm hatte. Es gibt sogar die spezielle Bezeichnung "Sonnensatellit" für solche Sonden. Damit ist meine Verwirrung aufgeklärt. Danke! --Neitram ✉ 15:22, 30. Okt. 2017 (CET)
- "Sonden" werden (nah) an den zu erkundenden Ort gebracht, was für Missionen an Lagrange-Punkten selten zutrifft, meist
(bisher immer?)handelt es sich um Teleskope. --Rainald62 (Diskussion) 15:10, 30. Okt. 2017 (CET)- en:List of objects at Lagrangian points spricht allerdings auch z.B. bei den Sonden des L2-Punkts von Sonne und Erde, wie etwa der Wilkinson Microwave Anisotropy Probe, von "probes", also Sonden -- auch wenn diese keine Sonden im strengen Sinn von "auf eine Reise hin zu einem Untersuchungsobjekt geschickt" sind. Ich vermute deshalb, der Begriff der Sonde kann auch etwas weiter gefasst werden. --Neitram ✉ 15:37, 30. Okt. 2017 (CET)
- Danke für den Link auf die Liste, es waren doch einige echte "Probes" darunter. Dass die dortigen Abschnittsüberschriften auf "Probe" lauten, ist aber kein gültiges Argument (und sollte geändert werden). --Rainald62 (Diskussion) 21:34, 30. Okt. 2017 (CET)
- Ja, es sind Satelliten des massereicheren Körpers. Bei richtigem Bezug wäre der Ausdruck "Satellit" also richtig, aber das müsste man ausdrücklich erwähnen. Ich habe zwischen "Raumsonde" und "Raumflugkörper" geschwankt, und mich dann für das erstere entschieden, nach kurzem Check im verlinkten Artikel Advanced Composition Explorer. Sollen wird das ändern? --Asdert (Diskussion) 16:31, 30. Okt. 2017 (CET)
- Fallweise ändern bitte. ACE ist klar eine Sonde (im Sonnenwind – übrigens heißen auch Elektroden, die man im Labor zwecks Messung diverser Parameter in ein Plasma hält, Sonden), SOHO klar nicht. Im allgemeinen Fall halte ich [[Satellit (Raumfahrt)|Forschungssatellit]] für angemessen. --Rainald62 (Diskussion) 21:34, 30. Okt. 2017 (CET)
- en:List of objects at Lagrangian points spricht allerdings auch z.B. bei den Sonden des L2-Punkts von Sonne und Erde, wie etwa der Wilkinson Microwave Anisotropy Probe, von "probes", also Sonden -- auch wenn diese keine Sonden im strengen Sinn von "auf eine Reise hin zu einem Untersuchungsobjekt geschickt" sind. Ich vermute deshalb, der Begriff der Sonde kann auch etwas weiter gefasst werden. --Neitram ✉ 15:37, 30. Okt. 2017 (CET)
- Alle fünf Lagrange-Punkte des Erde-Mond-Systems umkreisen die Erde, bezogen auf das nicht rotierende Universum. Die fünf Lagrange-Punkte des Erde-Mond-Systems ruhen nur in einem mit dem Mond mit rotierenden Bezugssystem. Bei den fünf Lagrange-Punkten des Sonne-Erde-Systems handelt es sich daher dann um Satelliten der Sonne. -- Karl Bednarik (Diskussion) 11:35, 30. Okt. 2017 (CET).
Sonnenfinsternis am Lagrange-Punkt L2
Am Lagrange-Punkt L2 von Sonne und Erde müsste die Erde ja stets direkt vor der Sonne stehen, also eine Art permanenter Sonnenfinsternis. Ist diese ringförmig? Wie viel Prozent der Sonnenscheibe wird an diesem Lagrange-Punkt von der Erde abgedeckt? --Neitram ✉ 15:44, 30. Okt. 2017 (CET)
- Von L2 beträgt der Abstand zur Erde 1,5 Mio.nbsp;km, der Abstand von Erde zur Sonne ist 150nbsp;Mionbsp;km. Von L2 aus gesehen verhalten sich die Entfernungen wie 101:1. Die Sonne hat einen Radius von 696.342 km die Erde einen von 6378 km, das ist ein Verhältnis von 109:1. Die Sonnenscheibe ist also ein Stück größer als die Erdscheibe. Rechnerisch komme ich auf 86% der Sonnenscheibe, die von der Erdscheibe abgedeckt wird, aber bei sind nicht genau kreisförmig und haben keinen definierten Rand. Kann das jemand nachrechnen? --Asdert (Diskussion) 16:44, 30. Okt. 2017 (CET)
- Das Verhältnis des Erdbahnradius von 149.600.000 km zum Sonnendurchmesser von 1.392.700 km beträgt rund 107,4. Das bedeutet, dass der Kernschatten der Erde 107,4-mal so lang wie der Durchmesser der Erde ist. Alle Bilder der Sonne, vom Erdbahnradius aus gesehen, sind immer 1/107,4-mal so klein wie die Brennweite der Optik. Der Äquatordurchmesser der Erde von 12.756 km mal 107,4 ergibt rund 1.369.994 km als Länge für den Kernschatten der Erde. Allerdings umkreisen Raumsonden auf den Lagrange-Punkten L1 und L2 diese Punkte auf einer Ellipsenbahn, deren Bahnebene quer zu der verlängerten Verbindungslinie der beiden Himmelskörper liegt, weil in dieser Richtung Rückstellkräfte vorhanden sind. Auf diese Weise können Raumsonden auf dem Sonne-Erde-Lagrange-Punkt L2 vermutlich sogar den Halbschatten der Erde vermeiden, was für ihre Photovoltaik günstig ist. -- Karl Bednarik (Diskussion) 09:07, 31. Okt. 2017 (CET).
- Der geplante Halo-Orbit des JWST:
- http://www.stsci.edu/jwst/overview/design/orbit
- -- Karl Bednarik (Diskussion) 11:02, 31. Okt. 2017 (CET).
- Der Durchmesser des Halbschattens der Erde in 1.369.994 km Entfernung sollte dann aus geometrischen Gründen rund 2 mal so groß sein wie der Durchmesser der Erde von 12.756 km. -- Karl Bednarik (Diskussion) 11:42, 31. Okt. 2017 (CET).
- Kein Objekt am L2 befindet sich stabil auf diesem Punkt. Sonnenfinsternis ist kein wirklich problematischer Punkt für die Stromversorgungn von Sonden an L2. Bei Gaia konnte jedoch schon eine Mondbedeckung mit den Sonnendetektoren registriert werden und die minimal veränderte Sonneneinstrahlung verursachte eine messbare Temperaturänderung, die die Messergebnisse beeinträchtigten. Aus diesem Grund wird man alles dafür tun, dass Gaia nie in den Halbschatten der Erde kommt. Man könnte wahrscheinlich ein paar Wochen von Messungen in die Tonne werfen.--Giftzwerg 88 (Diskussion)
- Danke für die Antworten. @Asdert: ich habe dazu diese Berechnung und Grafik gefunden. Mit den Zahlen
- scheinbarer Radius der Sonnenscheibe von L2 aus gesehen = 4590 μrad
- scheinbarer Radius der Erdscheibe von L2 aus gesehen = 4250 μrad
- kommt ebenfalls eine Bedeckung von ca. 87 % heraus, also eine ziemlich schöne ringförmige Sonnenfinsternis, wenn man exakt an L2 ist. Und korrekt, @Giftzwerg 88, Sonden auf Halo- oder Lissajous-Orbits um L2 sind ja nicht am genauen Lagrange-Punkt und können damit den Halbschatten der Erde auch komplett vermeiden -- so auch geschehen laut Gaia (Raumsonde)#Start und Testphase. --Neitram ✉ 16:08, 2. Nov. 2017 (CET)
- jau, den Abschnitt habe ich selbst formuliert. Ein schönes Gefühl, wenn man selbst zitert wird um zu beweisen, dass ich recht habe... Aber den Teil mit der Mondbedeckung muss ich noch in den Artikel schreiben.--20:03, 2. Nov. 2017 (CET)
Nur bei Exzentrizität nahe 0?
Gehe ich recht in der Annahme, dass es die Lagrange-Punkte nur dann gibt, wenn der masseärmere Körper den massereicheren Körper mit einer Exzentrizität nahe 0 umkreist, also auf einer annähernden Kreisbahn statt einer allgemeinen Keplerellipse? Wenn ja, dann sollte das m.E. unbedingt in den Artikel hinein. --Neitram ✉ 13:33, 3. Nov. 2017 (CET)
- Warum vermutest du das? --Rainald62 (Diskussion) 00:39, 5. Nov. 2017 (CET)
- Das vermute ich, weil in keiner Behandlung des Themas Lagrange-Punkte, die ich je gesehen habe, der allgemeine Fall der elliptischen Umlaufbahn behandelt wird. Alle Zeichnungen, die ich zum Thema der Lagrange-Punkte finden kann, zeigen immer den Fall der Kreisbahn. --Neitram ✉ 12:54, 6. Nov. 2017 (CET)
- Fast kein Objekt bewegt sich exakt auf einer Kreisbahn. Dieses bedeutet, dass auch Objekte auf einer Kepplerellipse Lagrange-Punkte haben. Für L1-L3 ist das ja unmittelbar einsichtig, allerdings wird sich der Punkt bei einer langgezogen Bahn im Jahresverlauf stärker bewegegen in Bezug zum masseärmeren Körper. Es gibt auch keinen Grund, warum die Berechnung für L4 und L6 kein Ergebnis für eine Ellipse haben soll, allerdings wird sich da wahrscheinlich auch der Winkel ändern. Die Formeln werden komplizierter.--Giftzwerg 88 (Diskussion) 18:01, 6. Nov. 2017 (CET)
- Das vermute ich, weil in keiner Behandlung des Themas Lagrange-Punkte, die ich je gesehen habe, der allgemeine Fall der elliptischen Umlaufbahn behandelt wird. Alle Zeichnungen, die ich zum Thema der Lagrange-Punkte finden kann, zeigen immer den Fall der Kreisbahn. --Neitram ✉ 12:54, 6. Nov. 2017 (CET)
- Wenn das hier korrekt ist, dann findet sich in The elliptical three-body problem - Triangular solution (1992) eine Behandlung des Themas. Demnach bewegen sich L4 und L5 so, dass sie stets äquidistant zu M2 und dem Baryzentrum von M1 und M2 sind (wenn M1 der massereiche und M2 der masseärmere Körper ist). --Neitram ✉ 09:47, 7. Nov. 2017 (CET)
Entfernung L2 von der Sonne
„Im Fall Sonne-Erde liegt der dritte Lagrange-Punkt auf der uns gegenüberliegenden Seite der Sonne, knapp 190 km weiter weg von der Sonne als die Erde.“. Wirklich so nah an der Sonne? NannoNanninga (Diskussion) 19:01, 20. Jan. 2019 (CET)
Entfernung L3 von der Sonne war gemeint NannoNanninga (Diskussion) 19:04, 20. Jan. 2019 (CET)
- Erde - Sonne: 149 597 870 km
- L3 - Sonne: 149 597 870 km + 190 km = 149 598 060 km
- L3 ist nicht nah an der Sonne. --Asdert (Diskussion) 23:12, 20. Jan. 2019 (CET)
Grafik 3 - Kritik
Im 3. Bild, Datei:ACE_at_L1.png
sind die Entfernungswerte nicht lesbar.
Die Exponenten von x 106 und x 108 sind unscharf verschwommen und dadurch in der Erstansicht am 13"-Bildschirm nicht lesbar.
Eine Formulierung mit "Mio." stattdessen wäre besser lesbar und breiter verständlich. --Helium4 (Diskussion) 11:48, 14. Jul. 2019 (CEST)











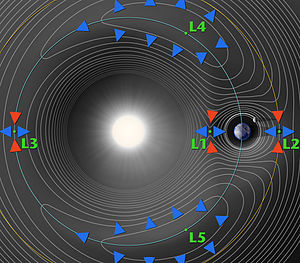






![{\displaystyle {\sqrt[{}]{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c952d258510266ee5546194a744ebb2d7b12c588)