RESET-Test nach Ramsey

Der RESET-Test nach Ramsey bzw. Test auf Fehlspezifikation der Regressionsgleichung nach Ramsey (englisch Ramsey Regression Equation Specification Error Test) ist ein von James B. Ramsey 1969 vorgeschlagener Test in der Statistik zur Überprüfung der Modellspezifikation im Rahmen der linearen Regression. Er prüft, ob nichtlineare Kombinationen der erklärenden Variablen $X_{i}$ einen Einfluss auf die erklärte Variable $Y$ haben. Falls die nichtlinearen Kombinationen der erklärenden Variablen einen Einfluss haben, dann sollte die lineare Modellspezifikation überdacht werden. Aber auch Fehlspezifikationen wie das Nichtberücksichtigen relevanter Variablen, Strukturbrüche, Homoskedastizität etc. können durch den Test angezeigt werden. Ein Vorteil des RESET-Test nach Ramsey ist es, dass kein explizites Alternativmodell spezifiziert werden muss; der Nachteil, dass er aber auch keinen Hinweis auf eine „richtige“ Spezifikation liefert.

Mathematische Formulierung

Im linearen Modell wird folgende Modellspezifikation angenommen

$Y=\beta _{0}+\beta _{1}X_{1}+\ldots +\beta _{m}X_{m}+\epsilon ,$

und man schätzt

${\hat {Y}}=b_{0}+b_{1}X_{1}+\ldots +b_{m}X_{m}.$

Der Test prüft, ob ein nichtlineares Modell der Form

$Y={\hat {Y}}+\gamma _{2}{\hat {Y}}^{2}+\ldots +\gamma _{k}{\hat {Y}}^{k}+\zeta$

nicht eine größere Erklärungskraft als das lineare Modell hat.

Die Hypothesen sind

$H_{0}:\gamma _{2}=\ldots =\gamma _{k}=0$ vs. $H_{1}:{\text{es existiert mindestens ein}}\;\gamma _{i}\neq 0$.

Die Teststatistik ist

${\frac {\frac {R_{1}^{2}-R_{0}^{2}}{k}}{\frac {1-R_{1}^{2}}{n-(m+k)-1}}}\sim F_{k-1;n-m-k}$

mit

• $R_{0}^{2}$: das Bestimmtheitsmaß des linearen Modells,
• $R_{1}^{2}$: das Bestimmtheitsmaß des nichtlinearen Modells,
• $n$: der Stichprobenumfang,
• $m$: die Anzahl der erklärenden Variablen und
• $k$: die Anzahl der zusätzlichen Parameter im nichtlinearen Modell.

Werden auch die Koeffizienten der linearen Regression im nichtlinearen Modell neu geschätzt und unterscheiden sie sich wesentlich von den geschätzten Koeffizienten im linearen Modell, so ist dies auch ein Hinweis auf eine Fehlspezifikation.

Der RESET-Test nach Ramsey lässt sich auch auf verallgemeinerte lineare Modelle erweitern.

Beispiel

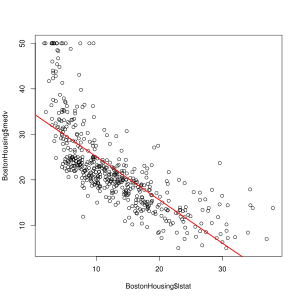
In den Boston-Housing-Daten wird der mittlere Kaufpreis von Häusern pro Bezirk (medv) in Abhängigkeit vom Anteil der Unterschichtbevölkerung (lstat) mittels einer einfachen linearen Regression geschätzt. Die Regressiongerade im Streudiagramm zeigt deutlich, dass der Zusammenhang zwischen den beiden Variablen nichtlinear ist.

Der RESET-Test nach Ramsey (mit ${\hat {y}}^{2}$ und ${\hat {y}}^{3}$) ergibt folgendes Ergebnis:

 RESET test
data:  linreg
RESET = 83.4103, df1 = 2, df2 = 502, p-value < 2.2e-16

Wie die Grafik bereits nahelegt, wird die Nullhypothese verworfen, da der p-Wert kleiner ist als z. B. ein Signifikanzniveau von $\alpha =5\,\%$.