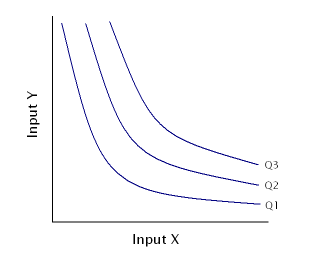
Isoquante
Als Isoquante bezeichnet man in der Mikroökonomik und dort speziell in der Theorie der Unternehmung eine spezielle Art von Isolinie.
Es gibt zwei gebräuchliche Definitionen des Begriffs Isoquante, diese ist entweder
- a) der geometrische Ort aller effizienten Kombinationen von Produktionsfaktoren, die den gleichen Output erzeugen, oder
- b) der geometrische Ort aller Kombinationen von Produktionsfaktoren, deren maximaler Output gleich groß ist.[1]
Definition
Wenn bei der Produktion nur zwei Faktoren verwendet werden, können Produktionsfunktionen graphisch durch Isoquanten dargestellt werden. Eine Isoquante ist die Menge aller Faktorkombinationen , die das gleiche maximale Outputniveau produzieren,
- .
Eine Produktionsfunktion ist durch ein System von Isoquanten definiert (analog dazu charakterisieren Indifferenzkurven eine Nutzenfunktion). Die Steigung einer Isoquante zeigt die Grenzrate der Substitution (kurz: GRS) an.[2] Sie lässt sich über den Satz von der impliziten Funktion bestimmen. Im Isoquantendiagramm ist eine Minimalkostenkombination als Tangentialpunkt von Isoquante und Isokostengerade zu erkennen.
Weblinks
Einzelnachweise
- ↑ Friedrich Breyer, Mikroökonomik. Eine Einführung, 5. Aufl., Springer 2011, S. 19.
- ↑ Jürgen Eichberger: Grundzüge der Mikroökonomik. 2004, S. 114.