Atmosphärischer Temperaturgradient
Der atmosphärische Temperaturgradient (auch Thermischer Höhengradient) ist der vertikale Temperaturgradient in der Erdatmosphäre. Vereinfachend gesagt wird durch ihn beschrieben, wie sehr die Lufttemperatur mit der Höhe zu- oder abnimmt.
Der horizontale Temperaturgradient, also vor allem zwischen dem Äquator und den Polen, wird als meridionaler Temperaturgradient bezeichnet. Er spielt eine wichtige Rolle als Antriebsfaktor der planetarischen Zirkulation bzw. im Energiehaushalt der Erde. Er ist von beiden Polen zum Äquator hin positiv, und zwar im Mittel von −33 °C (Südpol), beziehungsweise −23 °C (Nordpol) bis zu 26 °C (Äquator).
Der Temperaturgradient in den Schichten der Erdatmosphäre

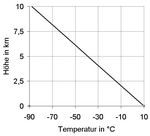
Betrachtet man die gesamte Erdatmosphäre in der Vertikalen, kehrt sich der atmosphärische Temperaturgradient (siehe rote Linie der nebenstehenden Grafik) insgesamt dreimal um, und zwar wie folgt:
- In der Troposphäre (bis ca. 15 km) ist er meist negativ, die Lufttemperatur nimmt also mit der Höhe ab (bis ca. −50 °C in Höhe der Tropopause). Sein regionaler Mittelwert beträgt −6 °C pro km. Im Detail ist das Ausmaß dieses Temperaturabfalls jedoch sehr unterschiedlich und kann sich in Teilbereichen auch in einen Temperaturanstieg umkehren (Inversionswetterlage). Der eigentlich messbare und damit statische Umgebungsgradient wird dabei von zwei dynamischen Gradienten bewegter Luftpakete unterschieden. Die beiden dynamischen Gradienten sind in ihrem Zusammenwirken mit dem statischen Gradienten der Zustandsluft für die Schichtungsstabilität der Troposphäre verantwortlich.
- In der Stratosphäre (ca. 15–50 km) ist der atmosphärische Temperaturgradient erst neutral (Isothermie bei ca. −50 °C) und nach oben hin positiv (Lufttemperatur steigt bis ca. 0 °C in Höhe der Stratopause).
- In der Mesosphäre (ca. 50–80 km) ist er erneut negativ (Lufttemperatur sinkt bis ca. −90 °C in Höhe der Mesopause).
- In der Thermosphäre (ca. 80–500 km) und der Exosphäre (>500 km) ist er wieder positiv (bis zu den Temperaturen im Weltall).
In der Meteorologie beschränkt man sich auf den Temperaturgradienten der Troposphäre und betrachtet meist auch nur dessen vertikale Komponente, also die Änderung der Lufttemperatur mit zunehmendem Abstand von der Erdoberfläche. Der Temperaturverlauf der darüber liegenden Atmosphärenschichten dagegen hat nur noch geringe Bedeutung für das Wetter.
Grundlagen
Theorie
Eng verbunden mit der Änderung der Temperatur in der Vertikalen sind einerseits die durch die Gravitation bedingte Änderung des Luftdrucks (siehe barometrische Höhenformel) und andererseits Energietransportvorgänge über die fühlbare und latente Wärme, also letztlich ein Übergang thermischer in potentielle Energie. Es handelt sich also um ein Phänomen, das nur auf Basis der Thermodynamik und der kinetischen Gastheorie erklärt werden kann. Als theoretische Grundlage dienen folglich die verschiedenen Gasgesetze. Für einfache Prozesse kann man die allgemeine Gasgleichung als Zustandsgleichung heranziehen, jedoch nur, solange die Luft ein annähernd ideales Verhalten zeigt.
Die Kopplung zwischen Druck und Temperatur hängt von der Zustandsänderung ab. Eine Luftdrucksenkung entspricht dabei einer Höhenzunahme sowie umgekehrt eine Luftdruckerhöhung einer Höhenabnahme.
Ein Luftpaket, das sich in der Atmosphäre vertikal nach oben oder unten bewegt, erfährt eine adiabatische Zustandsänderung, ihm wird also keine Wärme von außen zugeführt oder entzogen und es tritt auch keine Mischung mit der Umgebungsluft ein. Die adiabatische Temperaturänderung solcher Luftpakete ist einzig durch Druckabnahme beim Aufsteigen, beziehungsweise Druckzunahme beim Absinken bedingt. Diese Zirkulation ist vorhanden, weil die Strahlungsverhältnisse bei ruhender Atmosphäre einen Temperaturgradienten ergeben, der über dem adiabatischen Grenzwert liegt, die Luftschichtung also instabil wird und sich Zirkulation ergibt. Die adiabatische Annahme ist eine vereinfachende Annahme, die bei dynamischen Gradienten vorausgesetzt werden muss und hier aufgrund der geringen Mischungsfähigkeit sowie der schlechten Wärmeleitungseigenschaften meist in guter Näherung gültig ist. In Bodennähe zeigen sich jedoch die erwärmenden Effekte der Ausstrahlung, hier kann man also generell keinen adiabatischen Prozess veranschlagen. Zu berücksichtigen sind ferner dynamische Prozesse, wie zum Beispiel das Aufgleiten von Warmluft auf Kaltluft, die ebenfalls durch die Annahme eines adiabatischen Prozesses nicht erfasst werden. In der Stratosphäre liegt kein adiabatischer Gradient vor. Der Grund ist, dass der reine Strahlungstransport keinen Temperaturgradienten über dem adiabatischen Grenzwert ergibt. Aufgrund der Absorption der UV-Strahlung (Erwärmung) wird sogar der Temperaturgradient umgekehrt. Die Absorption der UV-Strahlung führt nicht nur zur Erwärmung, sondern auch zur Ozon-Bildung. Ein Temperaturgradient kleiner als der adiabatische Grenzwert gilt auch ganz allgemein für die höhere Atmosphäre, da das Strahlungsgleichgewicht hier generell dominiert – weil das Strahlungsgleichgewicht nicht den adiabatischen Grenzwert wie in der Troposphäre überschreitet.
Zum Vergleich von Temperaturwerten, die an unterschiedlichen Orten und Höhen gemessen wurden, bedient man sich der potentiellen Temperatur.
Veranschaulichung
Um zu verstehen, warum sich die Temperatur mit zunehmender Höhe ändert, hilft es, sich einen aufsteigenden Wetterballon vorzustellen. In diesem Gedankenexperiment ist es dann notwendig, den Ballon mit Luft zu füllen und (etwas weniger realistisch) anzunehmen, dass sich dessen Volumen beliebig ändern lässt, die Oberfläche also nicht starr ist und sich beliebig ausdehnen und zusammenziehen kann. Es handelt sich folglich um ein scharf begrenztes Luftpaket, das, isoliert von seiner Umgebung, langsam an Höhe gewinnt und sich adiabatisch ausdehnt. Am Boden wirkt der Luftdruck auf die Ballonhülle und presst diese auf ein bestimmtes Volumen zusammen. Mit zunehmender Höhe nimmt der Luftdruck jedoch ab und der Ballon dehnt sich aus, bis sein Innendruck dem der Umgebung entspricht. Obwohl dem Ballon weder Wärme zu- noch abgeführt wurde, hat sich die Temperatur der Luft im Ballon jetzt verändert. Wie kommt das? Adiabatisch bedeutet, dass zwar keine Wärme ausgetauscht wird, die Moleküle aber dennoch bei der Ausdehnung Volumenarbeit leisten auf Kosten ihrer kinetischen Energie.[1] Damit verringert sich die Innere Energie im Ballon, und zwar um den Betrag, der aufgebracht werden musste, um die Umgebungsluft zu verdrängen.
Betrachten wir dazu die physikalische Größe Temperatur. Eine Möglichkeit der Temperaturmessung beruht darauf, dass die Moleküle ihre kinetische Energie durch Stoß auf ein Messgerät übertragen (als Folge dehnt sich z. B. der Alkohol im Thermometer aus). Damit ist Temperatur, neben dem individuellen Gefühl eines jeden Menschen dafür, nichts anderes als ein makroskopisches Maß für die mittlere Bewegungsenergie der Atome und Moleküle, die Teil der Inneren Energie ist. Im Gegensatz zur Energie ist die Temperatur eine intensive Größe, also unabhängig von der Stoffmenge.
Mit der Ausdehnung des Ballons hat sich die kinetische Energie der Moleküle verringert, man misst eine geringere Temperatur der Luft im Ballon.
Betrachtet man andererseits ein Luftpaket in konstanter Höhe, das aber einer Luftdruckänderung ausgesetzt ist, dann führt dies zu einer Kompression oder Expansion und damit auch immer zu einer Änderung der Temperatur, da die bei der Volumenänderung umgesetzte Arbeit durch eine Änderung der Inneren Energie des Gases ausgeglichen werden muss.
Die Änderungen von Temperatur und Druck können selbst wieder Auswirkungen auf den Aggregatzustand der Bestandteile der Luft haben, denn diese kommen nur unter bestimmten Bedingungen als Gase vor. Dies zeigt sich beim Wasserdampf, denn nur er kann unter atmosphärischen Bedingungen zu flüssigem Wasser kondensieren oder zu Eis resublimieren. Da die dabei freiwerdende Wärme einen Einfluss auf die Temperatur hat, unterscheidet man zwischen trocken- und feuchtadiabatischen Temperaturgradienten.
Trockenadiabatischer Temperaturgradient
Der trockenadiabatische Temperaturgradient (Abkürzung DALR nach engl. dry adiabatic lapse rate) gilt für adiabatisch-reversible und damit isentrope Bedingungen, ohne dass es zu Änderungen des Aggregatzustands kommt. Er beträgt 9,76 Kelvin bzw. Grad Celsius je einem Kilometer Höhe und wird für Höhenänderungen eines Luftpaketes verwendet, solange die relative Luftfeuchtigkeit unter 100 Prozent bleibt, also keine Überschreitung des Taupunkts und folglich Kondensation erfolgt. Als Vereinfachung veranschlagt man meist einen Gradienten von einem Kelvin je hundert Meter. Von großer Bedeutung ist, dass dieser Wert, abgesehen von kleinen Schwankungen durch Unterschiede in der Luftzusammensetzung und Schwere, höhenunabhängig ist, die Ab- bzw. Zunahme der Temperatur also linear verläuft.
Die Herleitung des Gradienten basiert auf dem Ersten Hauptsatz der Thermodynamik (1.1) sowie der Annahme eines idealen Gases. Die Betrachtungen sind auf ein Mol bezogen.
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{d}U = \mathrm{d}Q + \mathrm{d}W = \mathrm{d}Q - p \cdot \mathrm{d}V}
|
(1.1)
| |
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{d}U = C_{\mathrm{m},V} \cdot \mathrm{d}T}
|
(1.2)
| |
Dabei ist Cm,V die molare Wärmekapazität der Luft bei konstantem Volumen. Lässt man die thermische Zustandsgleichung idealer Gase in differentieller Form einfließen (2.2), so erhält man nach Umformung und Gleichsetzung den Ausdruck (2.3).
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{d}Q = p \cdot \mathrm{d}V + C_{\mathrm{m},V} \cdot \mathrm{d}T}
|
(2.1)
| |
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p \cdot \mathrm{d}V + V \cdot \mathrm{d}p = R \cdot \mathrm{d}T}
|
(2.2)
| |
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{d}Q = R \cdot \mathrm{d}T + C_{\mathrm{m},V} \cdot \mathrm{d}T - V \cdot \mathrm{d}p}
|
(2.3)
| |
Mit der Beziehung (3.1) kann man die molare Wärmekapazität bei konstantem Druck Cm,p durch die molare Wärmekapazität bei konstantem Volumen Cm,V ersetzen, und mit Hilfe der allgemeinen Gasgleichung (3.2) wird das Volumen eliminiert und man erhält (3.3).
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle C_{\mathrm{m},p} = R + C_{\mathrm{m},V}}
|
(3.1)
| |
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p \cdot V = R \cdot T}
|
(3.2)
| |
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathrm{d}Q = C_{\mathrm{m},p} \cdot \mathrm{d}T - R \cdot T \cdot \frac{\mathrm{d}p}{p}}
|
(3.3)
| |
Für adiabatische Prozesse gilt dabei dQ = 0, was die Gleichung weiter vereinfacht und mit einer kleinen Umstellung zu Gleichung (3.4) führt.
(3.4)
| ||
Diese Gleichung kann nun mit der Barometrischen Höhenformel (4.1) gleichgesetzt werden, wobei dh für die Höhenänderung steht. Durch Kürzen und Umformen entsteht Gleichung (4.2).
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\mathrm{d}p}{p} = -\frac{g \cdot M}{R \cdot T} \, \mathrm{d}h}
|
(4.1)
| |
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle C_{\mathrm{m},p} \cdot \mathrm{d}T = -g \cdot M \cdot \mathrm{d}h}
|
(4.2)
| |
Löst man die Gleichung (4.2) nach dem Temperaturgradienten dT/dh = Γ auf, ergibt sich
Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Gamma = \frac{\mathrm{d}T}{\mathrm{d}h} = -\frac{g \cdot M}{C_{\mathrm{m},p}} = -\frac{g}{c_p}}
|
(4.3)
| |
Setzt man nun die spezifische Wärmekapazität der Luft bei konstantem Druck cp = 1,005 J/(g K) und die Fallbeschleunigung g = 9,81 m/s² ein, so erhält man für den trockenadiabatischen Temperaturgradienten Γ den Wert von −9,76 K/km.
Bei obigen Werten handelt es sich um jene der trockenen Luft, der recht variable Anteil des Wasserdampfs mit etwas anderen Stoffwerten wird also meist vernachlässigt. Bezieht man ihn in Form einer spezifischen Luftfeuchtigkeit von 0,01 mit ein, was ein recht typischer Wert ist, der als Durchschnitt gelten kann, so zeigt sich ein um 0,86 % niedrigerer Temperaturgradient. Unter der Voraussetzung, dass keine Kondensation auftritt, ist der Einfluss des Wasserdampfs also recht gering.
Eine Variante der Ableitung geht von der Adiabatengleichung Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle p^{(1-\kappa )}\cdot T^{\kappa }={\text{const.}}} aus.
Die logarithmische Form wird differenziert:
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\kappa-1}{\kappa} \cdot \frac{\mathrm{d}p}{p} = \frac{\mathrm{d}T}{T}}
Mit
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\mathrm{d}p}{p} = -\frac{M \cdot g}{R \cdot T} \cdot \mathrm{d}h}
aus der barometrischen Höhenformel erhält man
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\mathrm{d}T}{\mathrm{d}h} = \frac{1 - \kappa}{\kappa} \cdot \frac{M \cdot g}{R}}
M = 0,02896 kg/mol ist die Molmasse der Luft, g = 9,806 m s−2 die Normfallbeschleunigung und R = 8,314 J mol−1 K−1 die universelle Gaskonstante. Der Wert 1,4 für den Adiabatenexponenten berücksichtigt, dass Schwingungen an den Luftmolekülen nicht in nennenswertem Maß angeregt sind. Damit wird der Temperaturgradient der Trockenadiabate wie schon in Gleichung (4.3)
Feuchtadiabatischer Temperaturgradient
Für den feuchtadiabatischen Temperaturgradienten (Abkürzung MALR oder SALR nach engl.
bzw.
) gelten zwar ebenfalls adiabatische Bedingungen, doch dabei ausdrücklich für den Fall, dass eine Kondensation von Wasserdampf auftritt. Die im gasförmigen Aggregatzustand enthaltene Kondensationswärme (latente Wärme) von 2257 kJ/kg wird dadurch frei und erhöht die fühlbare Wärmeenergie der Luft. Der trockenadiabatische Temperaturgradient wird durch diese zusätzliche Energiezufuhr abgeschwächt. Wie stark diese Abschwächung des DALR ist, hängt von der Temperatur ab, denn je höher diese ist, desto größer ist auch der Anstieg der Sättigungsdampfdruckkurve, und desto mehr Wasserdampf kondensiert folglich auch pro Kelvin Abkühlung, d. h. desto mehr fühlbare Wärmeenergie wird pro Kelvin Abkühlung frei. Bei hohen Temperaturen kann er daher unter 4 K/km betragen, bei einer Temperatur von −40 °C mit 9 K/km aber auch dem trockenadiabatischen Gradienten recht nahekommen. In der rechten Abbildung ist ein idealisierter Temperaturverlauf mit einem konstanten Gradienten von 6,5 K/km dargestellt, was dem mitteleuropäischen Durchschnitt entspricht.
Umgebungsgradient
Der Umgebungsgradient, meist als geometrischer Temperaturgradient bezeichnet, stellt den eigentlichen Temperaturverlauf der Atmosphäre dar, so wie er von Radiosonden gemessen werden kann. Durch eine Vielzahl diabatischer, advektiver und konvektiver Prozesse kann er erheblich von den Modellvorstellungen eines trocken- oder feuchtadiabatischen Gradienten abweichen und auch deutlich um seinen eigenen Mittelwert streuen. Einen Gradienten, der größer ist als der trockenadiabatische, bezeichnet man dabei als überadiabatisch sowie dementsprechend einen niedrigeren Gradienten als unteradiabatisch. Als Symbol für den negativen geometrischen Gradienten mit dadurch positivem Zahlenwert wird γ verwendet.
Betrachtet man die gesamte Troposphäre, herrschen in unterschiedlichen Höhen zudem oft völlig unterschiedliche Gradienten, wobei sich in der Regel eine für die jeweilige Wetterlage charakteristische Abfolge einstellt. Auch eine Umkehr das Gradienten in Form einer Inversion ist dabei möglich. Aus den Dichteunterschieden, die sich zu einem Luftpaket ergeben, das adiabatisch über dynamische Gradienten erwärmt oder abgekühlt wird, leitet sich die Schichtungsstabilität der Erdatmosphäre ab.
Literatur
- Walter Roedel: Physik unserer Umwelt. Die Atmosphäre. 3., überarbeitete und aktualisierte Auflage. Springer, Berlin u. a. 2000, ISBN 3-540-67180-3.
- Hans Häckel: Meteorologie (= UTB für Wissenschaft. Uni-Taschenbücher 1338). 4., völlig überarbeitete und neugestaltete Auflage. Ulmer, Stuttgart (Hohenheim) 1999, ISBN 3-8252-1338-2.