Datei:01-Strahlensatz Anwendung Winkel.svg

Originaldatei (SVG-Datei, Basisgröße: 677 × 456 Pixel, Dateigröße: 134 KB)
![]()
Diese Datei und die Informationen unter dem roten Trennstrich werden aus dem zentralen Medienarchiv Wikimedia Commons eingebunden.
Inhaltsverzeichnis
Beschreibung
| Beschreibung01-Strahlensatz Anwendung Winkel.svg |
Deutsch: Näherungskonstruktion eines Winkels in Dezimalgrad mittels des dritten Strahlensatzes
English: Proximity construction of an angle in decimal degrees with the third intercept theorem |
| Datum | |
| Quelle | Eigenes Werk |
| Urheber | Petrus3743 |
| Andere Versionen |
 Proximity construction of the angle 4.153° with supplementary angle 175.847°  Proximity construction of the angle 45,371° with supplementary angle 134,629°  Proximity construction of the angle 88,546° with supplementary angle 91,454°  Basic construction (scheme) for the proximity construction of arbitrary angles 0° < α < 180° |
| SVG‑Erstellung InfoField |
Deutsch
Ein praktikables Beispiel für den dritten Strahlensatz in Kombination mit Zahlengeraden ist die Näherungskonstruktion eines Winkels in Dezimalgrad. Hierfür wird der Wert des Sinus oder des Kosinus vom gesuchten Winkel verwendet.
- Die Grundkonstruktion besteht aus einer Zahlengeraden s1, zwei zur Zahlengeraden s1 senkrecht stehenden parallelen Zahlengeraden s2, s3 jeweils mit zehn Teilungspunkten 0,1 bis 1,0 sowie einer Diagonalen ab 1,0 von s3 durch 0,1 von s2 bis zur Zahlengeraden s1; es ergibt sich dabei auf s1 der Scheitelpunkt E. Ein Viertelkreis um A ab 1,0 von s2 bis s1 bestimmt die Länge des ersten Winkelschenkels |A1,0| und schließt damit die Grundkonstruktion (Schema) ab.
- Für die Veranschaulichung der eigentlichen Konstruktion wurde der Winkel 57,14° mit seinem Sinuswert ca. 0,84 gewählt.
- Zuerst wird der Teilungspunkt 0,4 mit dem Scheitelpunkt E verbunden, dabei entsteht auf s2 der auf ein Zehntel verkleinerte Wert 0,04.
- Nun nimmt man den Abschnitt der Werte 0,1 und 0,04 (größere Zirkelöffnung) in den Zirkel und überträgt ihn auf s2 ab dem Teilungspunkt 0,9; somit ergibt sich der gewählte Sinuswert 0,84.
- Eine abschließende zur Zahlengeraden s1 parallele Linie ab dem Sinuswert 0,84 bis zum Viertelkreis ergibt den Schnittpunkt H für den zweiten Winkelschenkel |AH|. Der somit konstruierte Winkel 1,0AH hat den Näherungswert 57,14012...° mit einem absoluten Winkelfehler Fα ≈ 0,00012° < 1 Winkelsekunde =
= 0,00027°
- Werden die relevanten Teilungspunkte mit B, D, F und G bezeichnet, ergeben sich gemäß dem dritten Strahlensatz die Verhältnisse der Abschnitte:
und
- Absolute Fehler an der Sehne:
- F = Skonstr. - Stheor.
- F = 0,956465996 - 0,956464163 = 0,000001833
- Beispiel: Bei einem Radius von 1 km wäre der absolute Fehler an der Sehne ca. 1,8 mm.
English
A practical example for the third intercept theorem in combination with the number line is the proximity construction of an angle in decimal degrees. For this purpose, the value of the sine or the cosine of the angle being sought is used.
- The basic construction consists of a number line s1, two parallel number lines s2, s3 perpendicular to the number lines s1, each with ten division points 0.1 to 1.0 and one diagonal from 1.0 of s3 through 0.1 of s2 to the number line s1; this results in s1 the vertex E. A quarter circle around A from 1.0 from s2 to s1 determines the length of the first angle limb | A1,0 | and thus completes the basic construction (scheme).
- For the purpose of illustrating the actual construction, the angle 57.14° with its sine value was selected about 0.84.
- First, the divider point 0.4 is connected to the vertex E, resulting in a value reduced by one tenth from 0.04 on s2.
- Then the section of the values 0.1 till 0.04 (larger compass opening) is taken into the compass and transferred on s2 from the divider point 0.9; thus the selected sine value is obtained.
- A final line parallel to the number line s1 from the sine value 0.84 to the quarter circle gives the intersection H for the second angle limb |AH|. The thus constructed angle 1.0AH has the approximation value 57.14012...° with an absolute angle error Fα ≈ 0.00012° < 1 second of arc =
degree = 0,00027°
- If the relevant dividing points are designated by B, D, F and G, the ratios of the sections are obtained according to the third intercept theorem:
und
- Absolute error at the chord:
- F = Sconstr. - Stheor.
- F = 0.956465996 - 0.956464163 = 0.000001833
- Example: For a radius of 1 km, the absolute error at the chord would be about 1.8 mm.
Lizenz
- Dieses Werk darf von dir
- verbreitet werden – vervielfältigt, verbreitet und öffentlich zugänglich gemacht werden
- neu zusammengestellt werden – abgewandelt und bearbeitet werden
- Zu den folgenden Bedingungen:
- Namensnennung – Du musst angemessene Urheber- und Rechteangaben machen, einen Link zur Lizenz beifügen und angeben, ob Änderungen vorgenommen wurden. Diese Angaben dürfen in jeder angemessenen Art und Weise gemacht werden, allerdings nicht so, dass der Eindruck entsteht, der Lizenzgeber unterstütze gerade dich oder deine Nutzung besonders.
- Weitergabe unter gleichen Bedingungen – Wenn du das Material wiedermischst, transformierst oder darauf aufbaust, musst du deine Beiträge unter der gleichen oder einer kompatiblen Lizenz wie das Original verbreiten.
Kurzbeschreibungen
In dieser Datei abgebildete Objekte
Motiv
Einige Werte ohne einen Wikidata-Eintrag
27. Oktober 2016
image/svg+xml
6e24cacc9c802db8b3e2089083ee9d107149d1ba
136.977 Byte
456 Pixel
677 Pixel
Dateiversionen
Klicke auf einen Zeitpunkt, um diese Version zu laden.
| Version vom | Vorschaubild | Maße | Benutzer | Kommentar | |
|---|---|---|---|---|---|
| aktuell | 14:48, 12. Jan. 2019 | 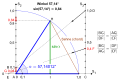 | 677 × 456 (134 KB) | wikimediacommons>Petrus3743 | (chord) nachgetragen |
Dateiverwendung
Keine Seiten verwenden diese Datei.
Metadaten
Diese Datei enthält weitere Informationen (beispielsweise Exif-Metadaten), die in der Regel von der Digitalkamera oder dem verwendeten Scanner stammen. Durch nachträgliche Bearbeitung der Originaldatei können einige Details verändert worden sein.
| Breite | 19.094891710708136cm |
|---|---|
| Höhe | 12.864209746032623cm |
