Zur Beschreibungsseite auf Commons

Datei:Discrete probability distribution illustration.png

aus Wikipedia, der freien Enzyklopädie

Originaldatei ‎(1.806 × 2.033 Pixel, Dateigröße: 44 KB, MIME-Typ: image/png)

Commons-logo.svg

Diese Datei und die Informationen unter dem roten Trennstrich werden aus dem zentralen Medienarchiv Wikimedia Commons eingebunden.

Zur Beschreibungsseite auf Commons

There are SVG versions:    Discrete distribution
Normal distribution
Mixed distribution

Beschreibung

Beschreibung
English: From top to bottom, the cumulative distribution function of a discrete probability distribution, continuous probability distribution, and a distribution which has both a continuous part and a discrete part. Cumulative distribution functions are examples of càdlàg functions.
Français : Fonctions de répartition d'une variable discrète, d'une variable diffuse et d'une variable avec atome, mais non discrète.
עברית: בשרטוט העליון מוצגת פונקציית ההצטברות של ההתפלגות הבדידה שלה שלושה ערכים אפשריים: {1}, {3} ו-{7} בהסתברות 0.2, 0.5 ו-0.3 בהתאמה. השרטוט האמצעי מציג את פונקציית ההצטברות של התפלגות רציפה, עובדה שניתן להסיק בשל רציפות הפונקציה על כל הטווח [0,1]. השרטוט התחתון מציג פונקציית הצטברות של התפלגות שהינה רציפה בחלקה ובדידה בחלקה.
Magyar: Az eloszlásfüggvények például càdlàg függvények.
Italiano: Le funzioni di ripartizione sono un esempio di funzioni càdlàg.
日本語: 上から順に、離散確率分布、連続確率分布、連続部分と離散部分がある確率分布の累積分布関数.
한국어: 이산 확률 분포, 연속 확률 분포, 이산적인 부분과 연속적인 부분이 모두 존재하는 분포에 대한 각각의 누적 분포 함수.
Polski: Od góry: dystrybuanta pewnego dyskretnego rozkładu, rozkładu ciagłego, oraz rozkładu mającego zarówno ciągłą, jak i dyskretną część.
Српски / srpski: Одозго на доле, функција расподеле дискретне случајне променљиве, непрекидне случајне променљиве, и случајне променљиве која има и непрекидне и дискретне делове.
Sunda: From top to bottom, the cumulative distribution function of a discrete probability distribution, continuous probability distribution, and a distribution which has both a continuous part and a discrete part.
Türkçe: Yukarıdan aşağıya doğru: bir ayrık olasılık dağılımı için, bir sürekli olasılık dağılımı için ve hem sürekli hem de ayrık kısımları bulunan bir olasılık dağılımı için yığmalı olasılık fonksiyonu. Üsten alta doğru. Bir aralıklı dağılım için, bir sürekli dağılım için ve hem sürekli bir kısmı hem de aralıklı bir kısmı bulunan bir dağılım için yığmalı dağılım fonksiyonları.
Українська: Зверху вниз: функція розподілу для дискретного розподілу ймовірностей, для неперервного розподілу та для розподілу що містить дискретну та неперервну частини.
Tiếng Việt: Từ trên xuống dưới, hàm phân phối tích tũy của một phân phối xác suất rời rạc, phân phối xác suất liên tục, và một phân phối có cả một phần liên tục và một phần rời rạc. Hàm phân bố tích lũy là một ví dụ của hàm số càdlàg.
Quelle Eigenes Werk
Urheber Oleg Alexandrov
Andere Versionen see above and below
 
Dieses Diagramm wurde mit MATLAB erstellt.
File:Discrete probability distribution illustration.svg ist eine vektorisierte Version dieses Bildes. Diese sollte an Stelle des Rasterbildes verwendet werden.
File:Discrete probability distribution illustration.png → File:Discrete probability distribution illustration.svg
Für weitere Informationen siehe Help:SVG.
In anderen Sprachen
Alemannisch ∙ Bahasa Indonesia ∙ Bahasa Melayu ∙ British English ∙ català ∙ čeština ∙ dansk ∙ Deutsch ∙ eesti ∙ English ∙ español ∙ Esperanto ∙ euskara ∙ français ∙ Frysk ∙ galego ∙ hrvatski ∙ Ido ∙ italiano ∙ lietuvių ∙ magyar ∙ Nederlands ∙ norsk bokmål ∙ norsk nynorsk ∙ occitan ∙ Plattdüütsch ∙ polski ∙ português ∙ português do Brasil ∙ română ∙ Scots ∙ sicilianu ∙ slovenčina ∙ slovenščina ∙ suomi ∙ svenska ∙ Tiếng Việt ∙ Türkçe ∙ vèneto ∙ Ελληνικά ∙ беларуская (тарашкевіца) ∙ български ∙ македонски ∙ нохчийн ∙ русский ∙ српски / srpski ∙ татарча/tatarça ∙ українська ∙ ქართული ∙ հայերեն ∙ বাংলা ∙ தமிழ் ∙ മലയാളം ∙ ไทย ∙ 한국어 ∙ 日本語 ∙ 简体中文 ∙ 繁體中文 ∙ עברית ∙ العربية ∙ فارسی ∙ +/−
Neue Vektorgrafik

Lizenz

Public domain Ich, der Urheberrechtsinhaber dieses Werkes, veröffentliche es als gemeinfrei. Dies gilt weltweit.
In manchen Staaten könnte dies rechtlich nicht möglich sein. Sofern dies der Fall ist:
Ich gewähre jedem das bedingungslose Recht, dieses Werk für jedweden Zweck zu nutzen, es sei denn, Bedingungen sind gesetzlich erforderlich.

Source code (MATLAB)

% plot a the cummulative distribution function for a
% (a) discrete distribution
% (b) continuous distribution
% (c) a distribution which has both a discrete and a continuous part

function main()

   clf; hold on; axis equal; axis off;
   L=4; h = 0.02;
   X=0:h:L;
   shift = 2;
   
   Y = [0*find(X < 0.2*L), 0.3+0*find( X >= 0.2*L & X < 0.4*L) 0.6+0*find(X >= 0.4*L & X < 0.8*L), 1+0*find(X>= 0.8*L)];
   plot_graph(X, Y, L, 0*shift)

   Y = 0.5*erf((4/L)*(X-L/2.5))+0.5;
   plot_graph(X, Y, L, shift);

   ds = 0.4;
   Y = 0.5*erf((2/L)*(X-L/1.5))+0.5;
   Y = Y + [0*find(X < ds*L) 0.4+0*find(X >= ds*L)]; Y = min(Y, 1);
   plot_graph(X, Y, L, 2*shift);

   % plot two dummy points to make matlab expand a bit the window before saving
   plot(L+0.15, 1.1, '*', 'color', 0.99*[1, 1, 1]);
   plot(-0.5, -2.1*shift, '*', 'color', 0.99*[1, 1, 1]);

   % save as eps
   saveas(gcf, 'Discrete_probability_distribution_illustration.eps', 'psc2')
   
function plot_graph(X, Y, L, shift)

   % settings
   N = length (X);
   tol = 0.1;
   thick_line = 3;
   thin_line = 2;
   small_rad = 0.07;
   red= [1, 0, 0];
   blue = [0, 0, 1];
   fs = 23;
   epsilon = 0.01;
   
% plot a blue box
   plot([0, L, L, 0, 0], [0, 0, 1, 1, 0]-shift, 'linewidth', thin_line, 'color', blue)

   % everything will be shifted down
   Y  = Y - shift;
   
   % if the given funtion has a jump, plot some balls. Otherwise plot a continous segment
   for i=1:(N-1)
      if abs(Y(i)-Y(i+1)) > tol
	 
	 ball       (X(i+1), Y(i+1), small_rad,                red);
	 empty_ball (X(i),   Y(i),   thin_line, 0.9*small_rad, red);

      else
	 plot([X(i)-epsilon, X(i+1)+epsilon], [Y(i), Y(i+1)], 'color', red, 'linewidth', thick_line);
      end
   end

   ball       (0, -shift, small_rad,             red);
   ball       (L, 1-shift, small_rad,             red);

%plot text
   small= 0.4;
   text(-small, 0-shift, '0', 'fontsize', fs)
   text(-small, 1-shift, '1', 'fontsize', fs)
   
   
function ball(x, y, r, color)
   Theta=0:0.1:2*pi;
   X=r*cos(Theta)+x;
   Y=r*sin(Theta)+y;
   H=fill(X, Y, color);
   set(H, 'EdgeColor', 'none');


function empty_ball(x, y, thick_line, r, color)
   Theta=0:0.1:2*pi;
   X=r*cos(Theta)+x;
   Y=r*sin(Theta)+y;
   H=fill(X, Y, [1 1 1]);
   plot(X, Y, 'color', color, 'linewidth', thick_line);

Kurzbeschreibungen

Ergänze eine einzeilige Erklärung, was diese Datei darstellt.

In dieser Datei abgebildete Objekte

Motiv

Dateiversionen

Klicke auf einen Zeitpunkt, um diese Version zu laden.

Version vomVorschaubildMaßeBenutzerKommentar
aktuell15:51, 12. Mai 2007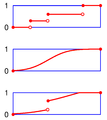Vorschaubild der Version vom 15:51, 12. Mai 20071.806 × 2.033 (44 KB)wikimediacommons>Oleg Alexandrov{{Information |Description= |Source=self-made |Date= |Author= User:Oleg Alexandrov }} Made with matlab. {{PD-self}}

Die folgende Seite verwendet diese Datei:

Abgerufen von „https://de.wikiup.org/wiki/Datei:Discrete_probability_distribution_illustration.png“