Datei:R'lyeh locations.png
aus Wikipedia, der freien Enzyklopädie

Größe dieser Vorschau: 600 × 600 Pixel. Weitere Auflösungen: 240 × 240 Pixel | 480 × 480 Pixel | 768 × 768 Pixel | 1.024 × 1.024 Pixel | 2.048 × 2.048 Pixel | 3.000 × 3.000 Pixel.
Originaldatei (3.000 × 3.000 Pixel, Dateigröße: 7,68 MB, MIME-Typ: image/png)
![]()
Diese Datei und die Informationen unter dem roten Trennstrich werden aus dem zentralen Medienarchiv Wikimedia Commons eingebunden.
Beschreibung
| BeschreibungR'lyeh locations.png |
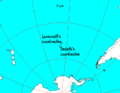
English: Locations of R'Lyeh, a fictional city that appeared in the writings of H. P. Lovecraft (†1937). Lovecraft claims R'lyeh is located at 47°9′S 126°43′W in the southern Pacific Ocean. While August Derleth, a contemporary correspondent of Lovecraft and co-creator of the Cthulhu Mythos, placed R'lyeh at 49°51′S 128°34′W. Both locations are close to the Pacific pole of inaccessibility (the "Nemo" point, 48°52.6′S 123°23.6′W), a point in the ocean farthest from any land mass. |
| Datum | |
| Quelle |
Eigenes Werk Dieser Plot wurde mit Matplotlib erstellt. |
| Urheber | Nojhan |
| Andere Versionen |
|

|
This map, as well as other fictitious maps, is fictitious or too incorrect (i.e. due to anachronism) to be used in real-life contexts (contemporary or historic). It may have some visual elements that are similar to official maps such as colors or certain layout features, but they are NOT official and don't have any official recognition. |
[[Category:]]
Source code
This image has been generated by the following source code in Python:
print "import modules...",
import sys
sys.stdout.flush()
import pickle
from mpl_toolkits.basemap import Basemap, shiftgrid, cm
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
from netCDF4 import Dataset
print "ok"
# Lovecraft: 47:9'S 126:43'W
lovecraft_lat = -47.9
lovecraft_lon = -126.43
# August Derleth: 49:51'S 128:34'W
derleth_lat = -49.51
derleth_lon = -128.34
# Nemo point: 48:52.6'S 123:23.6'W
nemo_lat = -48.526
nemo_lon = -123.236
# The Bloop:
# Appears to be way too far from the Nemo point to be interesting in a R'lyeh context
# bransfield_strait_lat=-63
# bransfield_strait_lon=-59
# ross_sea_lat = -75
# ross_sea_lon = -175
# cape_adare_lat = -71.17
# cape_adare_lon = -170.14
# Not necessary, because the default projection is ortho,
# but can be useful if you want another one.
def equi(m, centerlon, centerlat, radius, *args, **kwargs):
"""
Drawing circles of a given radius around any point on earth, given the current projection.
http://www.geophysique.be/2011/02/20/matplotlib-basemap-tutorial-09-drawing-circles/
"""
glon1 = centerlon
glat1 = centerlat
X = []
Y = []
for azimuth in range(0, 360):
glon2, glat2, baz = shoot(glon1, glat1, azimuth, radius)
X.append(glon2)
Y.append(glat2)
X.append(X[0])
Y.append(Y[0])
#m.plot(X,Y,**kwargs) #Should work, but doesn't...
X,Y = m(X,Y)
plt.plot(X,Y,**kwargs)
def shoot(lon, lat, azimuth, maxdist=None):
"""Shooter Function
Plotting great circles with Basemap, but knowing only the longitude,
latitude, the azimuth and a distance. Only the origin point is known.
Original javascript on http://williams.best.vwh.net/gccalc.htm
Translated to python by Thomas Lecocq :
http://www.geophysique.be/2011/02/19/matplotlib-basemap-tutorial-08-shooting-great-circles/
"""
glat1 = lat * np.pi / 180.
glon1 = lon * np.pi / 180.
s = maxdist / 1.852
faz = azimuth * np.pi / 180.
EPS= 0.00000000005
if ((np.abs(np.cos(glat1))<EPS) and not (np.abs(np.sin(faz))<EPS)):
alert("Only N-S courses are meaningful, starting at a pole!")
a=6378.13/1.852
f=1/298.257223563
r = 1 - f
tu = r * np.tan(glat1)
sf = np.sin(faz)
cf = np.cos(faz)
if (cf==0):
b=0.
else:
b=2. * np.arctan2 (tu, cf)
cu = 1. / np.sqrt(1 + tu * tu)
su = tu * cu
sa = cu * sf
c2a = 1 - sa * sa
x = 1. + np.sqrt(1. + c2a * (1. / (r * r) - 1.))
x = (x - 2.) / x
c = 1. - x
c = (x * x / 4. + 1.) / c
d = (0.375 * x * x - 1.) * x
tu = s / (r * a * c)
y = tu
c = y + 1
while (np.abs (y - c) > EPS):
sy = np.sin(y)
cy = np.cos(y)
cz = np.cos(b + y)
e = 2. * cz * cz - 1.
c = y
x = e * cy
y = e + e - 1.
y = (((sy * sy * 4. - 3.) * y * cz * d / 6. + x) *
d / 4. - cz) * sy * d + tu
b = cu * cy * cf - su * sy
c = r * np.sqrt(sa * sa + b * b)
d = su * cy + cu * sy * cf
glat2 = (np.arctan2(d, c) + np.pi) % (2*np.pi) - np.pi
c = cu * cy - su * sy * cf
x = np.arctan2(sy * sf, c)
c = ((-3. * c2a + 4.) * f + 4.) * c2a * f / 16.
d = ((e * cy * c + cz) * sy * c + y) * sa
glon2 = ((glon1 + x - (1. - c) * d * f + np.pi) % (2*np.pi)) - np.pi
baz = (np.arctan2(sa, b) + np.pi) % (2 * np.pi)
glon2 *= 180./np.pi
glat2 *= 180./np.pi
baz *= 180./np.pi
return (glon2, glat2, baz)
print "read in etopo5 topography/bathymetry"
url = 'http://ferret.pmel.noaa.gov/thredds/dodsC/data/PMEL/etopo5.nc'
etopodata = Dataset(url)
print "get data"
def topopickle(etopodata,name):
import sys
print "\t"+name+"...",
sys.stdout.flush()
filename = "rlyeh_"+name+".pickle"
try:
with open(filename,"r") as fd:
print "load...",
var = pickle.load(fd)
except IOError:
print "copy...",
var = etopodata.variables[name][:]
with open(filename,"w") as fd:
print "dump...",
pickle.dump(var,fd)
print "ok"
return var
topoin = topopickle(etopodata,"ROSE")
lons = topopickle(etopodata,"ETOPO05_X")
lats = topopickle(etopodata,"ETOPO05_Y")
print "shift data so lons go from -180 to 180 instead of 20 to 380...",
sys.stdout.flush()
topoin,lons = shiftgrid(180.,topoin,lons,start=False)
print "ok"
# create the figure and axes instances.
fig = plt.figure()
ax = fig.add_axes([0.1,0.1,0.8,0.8])
print "setup basemap"
# set up orthographic m projection with
# perspective of satellite looking down at 50N, 100W.
# use low resolution coastlines.
m = Basemap(projection='ortho',lat_0=nemo_lat,lon_0=nemo_lon,resolution='l')
m.bluemarble()
# Generic Mapping Tools colormaps:
# GMT_drywet, GMT_gebco, GMT_globe, GMT_haxby GMT_no_green, GMT_ocean, GMT_polar,
# GMT_red2green, GMT_relief, GMT_split, GMT_wysiwyg
print "transform to nx x ny regularly spaced native projection grid"
# step=5000.
step=10000.
nx = int((m.xmax-m.xmin)/step)+1; ny = int((m.ymax-m.ymin)/step)+1
topodat = m.transform_scalar(topoin,lons,lats,nx,ny)
print "plot topography/bathymetry as shadows"
from matplotlib.colors import LightSource
ls = LightSource(azdeg = 45, altdeg = 220, hsv_min_val=0.0, hsv_max_val=1.0,
hsv_min_sat=0.0, hsv_max_sat=1.0)
# convert data to rgb array including shading from light source.
# (must specify color m)
rgb = ls.shade(topodat, cm.GMT_ocean)
im = m.imshow(rgb, alpha=0.15)
print "draw coastlines, country boundaries, fill continents"
m.drawcoastlines(linewidth=0.25)
# draw the edge of the map projection region
m.drawmapboundary(fill_color='white')
# draw lat/lon grid lines every 30 degrees.
m.drawmeridians(np.arange( 0,360,30), color="black" )
m.drawparallels(np.arange(-90,90 ,30), color="black" )
print "draw points"
psize=5
font = {'family' : 'serif',
'weight' : 'normal',
'size' : 18}
matplotlib.rc('font', **font)
x,y = m( lovecraft_lon, lovecraft_lat )
m.scatter(x,y,psize,marker='o', color='white')
plt.text(x+50000,y+50000+50000, "Lovecraft", color='white')
x,y = m( derleth_lon, derleth_lat )
m.scatter(x,y,psize,marker='o',color='white')
plt.text(x+50000-120000,y+50000, "Derleth", color='white', horizontalalignment="right")
x,y = m( nemo_lon, nemo_lat )
m.scatter(x,y,psize*3,marker='+',color='#555555')
plt.text(x+50000+50000,y+50000-80000, "Nemo", color="#555555", verticalalignment="top")
equi(m, nemo_lon, nemo_lat, radius=2688, color="#555555" )
# x,y = m( bransfield_strait_lon, bransfield_strait_lat )
# m.scatter(x,y,psize*3,marker='+',color='#555555')
# plt.text(x+50000+20000,y+50000-80000, "bransfield_strait", color="#555555", verticalalignment="baseline")
# x,y = m( ross_sea_lon, ross_sea_lat )
# m.scatter(x,y,psize*3,marker='+',color='#555555')
# plt.text(x+50000+20000,y+50000-80000, "ross_sea", color="#555555", verticalalignment="baseline")
# x,y = m( cape_adare_lon, cape_adare_lat )
# m.scatter(x,y,psize*3,marker='+',color='#555555')
# plt.text(x+50000+20000,y+50000-80000, "cape_adare", color="#555555", verticalalignment="baseline")
plt.savefig("R'lyeh_locations.png", dpi=600, bbox_inches='tight')
# plt.show()
| Kameraposition | 47° 54′ 00″ S, 126° 25′ 48″ W | Dieses und weitere Bilder auf OpenStreetMap |
|---|
Lizenz
Ich, der Urheber dieses Werkes, veröffentliche es unter der folgenden Lizenz:
Diese Datei ist unter der Creative-Commons-Lizenz „Namensnennung – Weitergabe unter gleichen Bedingungen 3.0 nicht portiert“ lizenziert.
- Dieses Werk darf von dir
- verbreitet werden – vervielfältigt, verbreitet und öffentlich zugänglich gemacht werden
- neu zusammengestellt werden – abgewandelt und bearbeitet werden
- Zu den folgenden Bedingungen:
- Namensnennung – Du musst angemessene Urheber- und Rechteangaben machen, einen Link zur Lizenz beifügen und angeben, ob Änderungen vorgenommen wurden. Diese Angaben dürfen in jeder angemessenen Art und Weise gemacht werden, allerdings nicht so, dass der Eindruck entsteht, der Lizenzgeber unterstütze gerade dich oder deine Nutzung besonders.
- Weitergabe unter gleichen Bedingungen – Wenn du das Material wiedermischst, transformierst oder darauf aufbaust, musst du deine Beiträge unter der gleichen oder einer kompatiblen Lizenz wie das Original verbreiten.
Kurzbeschreibungen
Ergänze eine einzeilige Erklärung, was diese Datei darstellt.
Возможное расположение города Р'Льеха, основываясь на версиях Лавкрафта и Дерлета
In dieser Datei abgebildete Objekte
Motiv
Einige Werte ohne einen Wikidata-Eintrag
10. Februar 2013
47°54'0"S, 126°25'48"W
Dateiversionen
Klicke auf einen Zeitpunkt, um diese Version zu laden.
| Version vom | Vorschaubild | Maße | Benutzer | Kommentar | |
|---|---|---|---|---|---|
| aktuell | 20:49, 12. Feb. 2013 |  | 3.000 × 3.000 (7,68 MB) | wikimediacommons>Nojhan | High resolution, draw the radius of the oceanic pole of inaccessibility, even more larger font, remove the bloop location, that appeared to be wrong. |
Dateiverwendung
Die folgenden 2 Seiten verwenden diese Datei:
Metadaten
Diese Datei enthält weitere Informationen (beispielsweise Exif-Metadaten), die in der Regel von der Digitalkamera oder dem verwendeten Scanner stammen. Durch nachträgliche Bearbeitung der Originaldatei können einige Details verändert worden sein.
| Horizontale Auflösung | 236,22 dpc |
|---|---|
| Vertikale Auflösung | 236,22 dpc |
Abgerufen von „https://de.wikiup.org/wiki/Datei:R%27lyeh_locations.png“