Unscharfe Suche
Die unscharfe Suche, auch Fuzzy-Suche oder Fuzzy-String-Suche genannt, umfasst in der Informatik eine Klasse von String-Matching-Algorithmen, also solchen, die eine bestimmte Zeichenkette (englisch string) in einer längeren Zeichenkette oder einem Text suchen bzw. finden sollen.
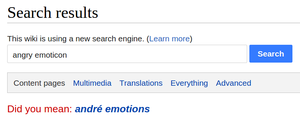
Typisch für die „unscharfe“ (englisch fuzzy) Suchmethode ist dabei, dass nicht die exakte Zeichenfolge als Suchkriterium zugrunde gelegt werden muss, sondern auch ähnliche Zeichenketten[1] gefunden werden sollen.[2] Ein bekanntes Maß zur Berechnung dieser Ähnlichkeit ist die sogenannte Levenshtein-Distanz; sie gibt an, wie viele Operationen – Löschen, Einfügen und Ersetzen – von Buchstaben in Wörtern nötig sind, um einen String aus dem anderen herzuleiten: Je weniger Operationen benötigt werden, desto ähnlicher sind beide Strings.[3] Eine andere Möglichkeit beruht auf sogenannten N-Grammen[4], mittels derer über bestimmte Wahrscheinlichkeiten berechnet wird, welche Buchstaben- oder Zeichenkettenkombination auf eine andere folgen könnte. Ein weiterer Ansatz gründet nicht direkt auf der grafischen Repräsentation eines Wortes, sondern es wird nach Zeichenfolgen gesucht, die gleich klingen: die phonetische Suche. Ein in diesem Zusammenhang bekanntes Verfahren für die Englische Sprache, das Wörter ihrem Klang nach indiziert, ist der Soundex-Algorithmus.[5]
Beide Ansätze erlauben es, gesuchte Zeichenketten auch dann zu finden, wenn zum Beispiel die genaue Schreibweise eines Namens oder Ausdrucks nicht bekannt ist, flektierte Formen eines Wortes gefunden oder auch fehlertolerante Suchergebnisse akzeptiert werden sollen. Verwendet wird die Fuzzy-Suche beispielsweise in Datenbanken[6], Suchmaschinen[7] oder computerlinguistischen Anwendungen.
Praxisbeispiele
Bei der Suche in Datenbanken können fehlertolerante Suchwerkzeuge unter Anwendung von String-Matching-Algorithmen Tipp- und Rechtschreibfehler ausgleichen. Ähnlichkeiten zwischen dem eingegebenen Suchbegriff und den Einträgen in der Datenbank werden auch ohne hinterlegte Wortlisten ermittelt. Treffer können nach Relevanz und Nähe zum Suchbegriff sortiert ausgegeben werden. Die Suche nach dem Begriff „Levensstein“ würde beispielsweise auch Einträge zu „Levenshtein“ finden. Werden Synonym-Listen hinterlegt, findet die unscharfe Suche beispielsweise zu dem Begriff „Fernseher“ auch Begriffe wie „Fernsehgerät“.
Die Anwendung aufwändiger String-Matching-Verfahren, wie dem Levenshtein-Algorithmus, geht in der Regel mit einem enormen Berechnungsaufwand einher[8] und führt bei großen Datenmengen zu einer oft hohen zeitlichen Verzögerung.
Beispielsweise in der Bioinformatik, werden Gensequenzen mit Gendatenbanken abgeglichen. Eine bekannte Sammlung von Algorithmen hierfür ist Blast.
Einzelnachweise
- ↑ Jan Petzold: Größere Datenmengen mit JavaScript performant durchsuchen. In: heise Developer. Heise Medien GmbH & Co. KG, 13. März 2015, abgerufen am 29. April 2020: „Ungenaue Suche (Fuzzy): Das Suchergebnis enthält auch Elemente, die dem Suchbegriff ähneln. Sie wird meist in Autocomplete-Feldern oder als Suchvorschlag verwendet (z. B. "Entwckler" findet auch "Entwickler").“
- ↑ Fuzzy-Suche. In: IT-Wissen.info. DATACOM Buchverlag GmbH, abgerufen am 29. April 2020: „Die Fuzzy-Search ist eine unscharfe oder fehlertolerante Suche. Im Gegensatz zu einer exakten Suche werden bei der Fuzzy-Suche auch dann Ergebnisse angezeigt, wenn das Suchwort fehlerhaft eingegeben wurde oder wenn die exakte Schreibweise des Suchwortes nicht bekannt ist.“
- ↑ Sonja Franz: Wie Suchalgorithmen funktionieren: Die Levenshtein-Distanz. In: interger_net. integer_net GmbH, 22. Februar 2018, abgerufen am 29. April 2020: „Die Levenshtein-Distanz beschreibt die minimale Anzahl von Änderungen, die nötig ist, um aus der ersten Zeichenkette die zweite Zeichenkette zu generieren. Als Änderungen gelten Hinzufügen, Entfernen und Austauschen von Zeichen. Sie ist benannt nach dem russischen Mathematiker Vladimir Levenshtein (1935–2017).“
- ↑ Tillmann Wegst: Stringähnlichkeit. In: Tillmann Wegst // Software-Entwicklung. 22. Januar 2006, abgerufen am 29. April 2020: „N-Gramm-Übereinstimmungen sind ein weiteres und sehr gebräuchliches Maß. Ein N-Gramm ist eine Folge benachbarter Elemente, im Fall von Strings also aufeinanderfolgender Schriftzeichen. "N" bezeichnet die Länge der verwendeten Folgen; üblich sind Trigramme, also N-Gramme mit Länge 3. Zur Ähnlichkeitsbestimmung werden zwei Strings in die in ihnen enthaltenen N-Gramme zerlegt, und die Größe der Schnittmenge der beiden N-Gramm-Mengen liefert den Wert für die Ähnlichkeit der Strings.“
- ↑ Rob Gravelle: MySQL Fuzzy Text Searching Using the SOUNDEX Function. In: DATABASE Journal. QuinStreet Inc., 9. März 2015, abgerufen am 29. April 2020 (englisch): „Soundex is a phonetic algorithm for indexing names by sound, as pronounced in English. SOUNDEX codes from different strings can be compared to see how similar the strings sound when spoken.“
- ↑ Ernst August Wieden: Unscharfe Suche in Datenbanken – konzeptuelle Grundlagen, Systementwurf und prototypische Implementierung. (pdf) In: Diplomarbeit. Technische Universität Hamburg-Harburg - Arbeitsbereich Softwaresysteme, August 2002, abgerufen am 30. April 2020: „Diese Arbeit verfolgt das Ziel, den Abfragemechanismus von Datenbanken intelligenter zu gestalten; dies insbesondere in Hinblick auf den Einsatz von Fuzzy-Logic-Methoden, die bisher vorwiegend Einsatz in der Regelungstechnik finden.“
- ↑ Stefan Krempl: Fuzzy Logic erobert das Internet. In: heise online. Heise Medien GmbH & Co. KG, 4. Mai 2005, abgerufen am 30. April 2020: „"In den kommenden Jahren wird das Internet das wichtigste Anwendungsgebiet von Fuzzy Logic sein", erklärte Lotfi Zadeh in einem Vortrag an der TU Berlin. Der emeritierte Informatikprofessor der University of California in Berkeley geht davon aus, dass sich die teilweise noch recht "dummen" Suchmaschinen in hilfreiche Diener verwandeln, die fix auf alle erdenklichen Fragen eine passende Antwort finden. Dazu müssten sie aber erst die natürliche Sprache der Menschen "verstehen", was am besten mit Fuzzy Logic zu bewerkstelligen sei.“
- ↑ Benno Nieswand: Levenshtein-Algorithmus - Wie funktioniert der Levenshtein-Algorithmus...? In: Levenshtein. Abgerufen am 29. April 2020: „Obwohl ausgeklügelte Verbesserungen bezglich der Berechnung grosser Matrizen gemacht wurden, gibt es keine Alternative zu dem meist recht großen Berechnungsaufwand.“