Rückkopplung

Der Fliehkraftregler als klassisches Beispiel für eine Rückkopplung: Je schneller die Maschine dreht, desto weiter werden die Kugeln nach außen geschleudert, wodurch mithilfe des Gestänges die Drosselklappe mehr schließt, was eine Verlangsamung der Maschine nach sich zieht: Ein Gleichgewichtszustand pendelt sich ein.

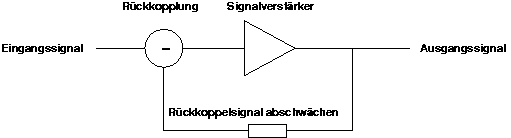
Eine Rückkopplung, auch Rückkoppelung, Rückmeldung oder Feedback [ˈfiːdˌbæk] (engl.), ist ein Mechanismus in signalverstärkenden oder informationsverarbeitenden Systemen, bei dem ein Teil der Ausgangsgröße direkt oder in modifizierter Form auf den Eingang des Systems zurückgeführt wird.

Arten

Rückkopplungen kommen in vielen technischen, biologischen, geologischen, wirtschaftlichen und sozialen Systemen vor. Je nach Art und Richtung der rückgeführten Größe kommt es zur Selbstverstärkung des durch das System bedingten Prozesses oder zu dessen Abschwächung oder Selbstbegrenzung. Im ersten Fall spricht man von positiver Rückkopplung oder Mitkopplung, im letzteren Fall von Gegenkopplung oder negativer Rückkopplung.

In technischen Systemen wird häufig angestrebt, Rückkopplungsvorgänge nicht nur durch die Kapazität der beteiligten Energiespeicher zu begrenzen, sondern auch eine Struktur zu schaffen, die durch passive und aktive Gegenkopplung Überlastungen verhindert. Dabei handelt es sich oft um Regelungsvorgänge.

In der Natur können Rückkopplungen in komplexen Strukturen vorkommen, in denen Elemente über andere, zum Teil entfernt gelegene Systeme, wieder auf sich selbst zurückwirken.

In psychologisch determiniertem Verhalten ist die Richtung der Rückkopplung nicht von vornherein festgelegt. So kann zum Beispiel im System Lernen in der Schule eine schlechte Notenwertung je nach Motivation sowohl zu erhöhtem Fleiß (Gegenkopplung) oder im Gegenzug auch zur Resignation führen (Mitkopplung, bzw. verstärkende Wirkung).

Mitkopplung

In einer Lockerschneelawine reißt der in Bewegung gekommene Schnee in einem Mitkopplungsprozess noch mehr Schnee mit sich, der wiederum das Phänomen weiter anschwellen lässt

→ Hauptartikel: Positive Rückkopplung

Bei der Mitkopplung kommt eine vorzeichen- oder phasenrichtige Rückführung der Ausgangsgröße im Zusammenspiel mit verstärkenden Elementen des Systems zum Tragen. Dies kann nützlich sein, beispielsweise um Reibungsverluste auszugleichen, es kann aber auch eine Gefahr darstellen, denn die beteiligten Größen können hierbei gefährlich anwachsen, solange dazu Energie bereitgestellt wird, und es kann, wenn nicht zusätzliche, auf den Prozess dämpfend einwirkende Größen wirksam werden, zu einer Zerstörung kommen. Hierbei wird der Vorgang nur noch durch die Begrenzung der (Energie-)Ressourcen limitiert.

In technischen Systemen spricht man von einer ungedämpften periodischen Schwingung in Resonanz oder einer aperiodischen Schwingung. Je nachdem, ob es zu einem lawinenartigen Anschwellen im System kommen kann oder nicht, unterscheidet man zwischen unterkritischer, kritischer oder überkritischer Mitkopplung.

Positive Rückkopplung findet man oft bei Wachstumsprozessen. Man spricht in nichttechnischen Systemen auch von einem circulus virtuosus, oder, wenn das Ergebnis als solches nicht gewünscht wird, auch von einem Teufelskreis oder Circulus vitiosus.

Beispiele: Schuldenfalle, Kettenreaktion, Autokatalyse, Akustische Rückkopplung, Börsencrash, elektronische Schaltungen wie z. B. Schmitt-Trigger oder Oszillatoren (Meißner-Schaltung zur Realisierung eines ungedämpften Schwingkreises), Benjamin-Franklin-Effekt der Sozialpsychologie

Gegenkopplung

Beispiel einer Gegenkopplung:
Eine Heizung und ein Kaltleiter (PTC)

→ Hauptartikel: Negative Rückkopplung

Bei der Gegenkopplung ist eine Rückführung des Ausgangssignals mit negativem Vorzeichen bzw. gegenphasiger Polarität wirksam. Diese negative Rückführung wirkt der äußeren Anregung entgegen und führt zu einer sich verringernden Zustandsänderung. Solche Systeme neigen entweder stark zum Einnehmen einer stabilen Lage oder zu mehr oder weniger abklingenden Schwingungsverhalten um einen stabilen Mittelwert.

Die Gegenkopplung ist ein fundamentales Prinzip in der gesamten belebten Natur und verbreitet in technischen Systemen. Insbesondere die Regelungstechnik hat das Ziel, die Gegenkopplung so einzurichten, dass ein stabiles Systemverhalten erreicht wird. Dazu werden in technischen Systemen automatische Regler verwendet.

Unerwünschte Schwingneigung in einem Regelkreis kann beispielsweise durch variable Dimensionierung der Gegenkopplung vermieden werden, indem die Verstärkung mit zunehmender Frequenz verringert wird.

Das kennzeichnende Merkmal in natürlichen Systemen sind Rückkopplungsschleifen mit Selbstregulationseigenschaften. In biologischen Systemen von Organismen ist dieses Prinzip entscheidend bei der Homöostase. Gegenkopplung spielt eine Rolle in allen (Selbst-)Erhaltungsprozessen.

Selbsterregung (d. h. das initiale Entstehen von Schwingungen) tritt ein, wenn zunächst eine positive Kopplung und dann verzögert eine negative Kopplung einsetzt. Die Systemparameter pendeln dann zwischen Ruhe und typischen Höchstwerten. Dieser Fall kann insbesondere in elektronischen Regelkreisen bei hohen Frequenzen eintreten, wenn die Phasenbedingung für eine Gegenkopplung aufgrund zufälliger Phasenverschiebungen aller Komponenten nicht mehr zuverlässig gegeben ist.

Beispiele: Fliehkraftregler, das Füllen eines Eimers mit einem Loch im Boden, selbstregelnde Vorgänge in Ökosystemen, Gegenkopplung in Reglern und Verstärkern, Aussetzen von Nützlingen, Drehstrommotoren, Boiler mit Thermostat, Kühlschrank, Körperwärme-Regulation bei Säugetieren, Preisbildung durch Angebot und Nachfrage

Beispiele mit variablem Schwingungsverhalten: Räuber-Beute-Beziehung, Rhythmus der Cortison-Sekretion, zirkadiane biologische Rhythmen, Menstruationszyklus, Konjunkturzyklen, Regelschwingungen (Instabilität) von Reglern, Selbsterregung von Verstärkern (aufgrund ungeeigneter Gegenkopplung, unzureichender Abschirmung zwischen Ein- und Ausgang oder ungeeigneten Lasten)

Stabilität, Gegenkopplungsgleichungen der Übertragungsfunktion, Numerik

Die Berechnung eines Systems mit der Gegenkopplung setzt ein lineares dynamisches System $G(s)$ mit Zeitverhalten voraus, das einen Signaleingang und einen Signalausgang aufweist. Dabei ist die unabhängige Variable die Zeit.

Die Regelgröße eines Regelkreises zeigt ein völlig unterschiedliches Verhalten, wenn der Gegenkopplungspfad $G_{2}$ verstärkende, differenzierende oder integrierende (verzögernde) Eigenschaften zeigt. Die mathematischen Beziehungen aller dynamischen Teilsysteme werden als lineare Übertragungssysteme G(s) dargestellt.

Wird der Ausgang eines dynamischen Systems, bestehend aus mindestens 3 Teil-Verzögerungssystemen $G(s)$ und den Zeitkonstanten $T=1$ und der Verstärkung $K\geq 8$, direkt auf den Signaleingang des Systems mit negativem Vorzeichen additiv zurückgeführt (Gegenkopplung), dann kehrt sich für eine beliebige Führungsgröße die Gegenkopplung in eine Mitkopplung um und es entstehen Dauerschwingungen mit steigenden Amplituden.

Die Gesamtübertragungsfunktion $G_{ges}(s)$ eines Regelkreises ergibt sich aus den Übertragungsfunktionen der Pfade $G_{1}$ und $G_{2}$.

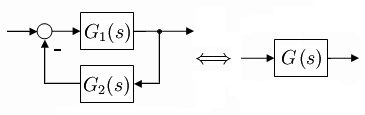
Gegenkopplung mit Teilsystem G₂(s) im Rückführungspfad

Das Verhalten der Ausgangsgröße im Pfad $G_{1}$ des Systems hängt davon ab, ob der Pfad $G_{2}$ verstärkende, verzögernde oder differenzierende Funktionen erhält.

• Verzögernde Systeme in der Gegenkopplung (z. B. die Messeinrichtung der Regelgröße) bewirken verzögernden Aufbau der Regelgröße oder gedämpfte Überschwingungen.
• Differenzierende Systeme in der Gegenkopplung bewirken eine Kompensation von Verzögerungsanteilen im Vorwärtszweig $G_{1}$, bzw. eine Reduzierung bei gegebenen Überschwingungen.
• Ein Verstärkungsfaktor $K\geq 1$ in der Gegenkopplung reduziert die Regelgröße um ${\frac {y(t)}{K}}$.

Die Übertragungsfunktion des geschlossenen Kreises mit Teilsystemen in der Rückkopplung lautet:

$G_{ges}\left(s\right)={\frac {G_{1}\left(s\right)}{1+G_{1}\left(s\right)\cdot G_{2}\left(s\right)}}$

Diese Gleichung zeigt, eine Pol-Nullstellenkompensation als Systemkompensation kann für den Vorwärtspfad $G_{1}$ nicht im Gegenkopplungspfad $G_{2}$ angewendet werden.

Gegenkopplung ohne Teilsystem G₂(s) im Rückführungspfad

Einfacher Regelkreis mit der Rückkopplung $G_{2}=1$

Bei einem Übertragungssystem (Regelkreis), der in dem Gegenkopplungszweig kein statisches oder dynamisches Teilsystem enthält, ergibt das System $G_{2}=1$.

Die Übertragungsfunktion des geschlossenen Kreises ohne Teilsysteme in der Gegenkopplung lautet:

$G_{ges}(s)={\frac {G_{1}(s)}{1+G_{1}(s)}}$

Mathematische Methoden zur Berechnung eines Regelkreises

Die einfachste Methode der Berechnung eines Regelkreises ist die Simulation der einzelnen Teil-Übertragungsfunktionen $G(s)\ \to \ G_{k}$ des aufgeschnittenen Regelkreises und die Schließbedingung $e_{k}=w_{k}-y_{k}$ der Regelabweichung.

Gewöhnliche lineare Differenzialgleichungen, die z. B. ein dynamisches System 1. Ordnung wie:

$a_{1}\cdot y'(t)+a_{0}\cdot y(t)=b_{0}\cdot u(t)$

beschreiben, können nach dem Differenzenverfahren relativ einfach in eine Differenzengleichung überführt werden. Dies geschieht dadurch, dass die Differenzialquotienten der Differenzialgleichung direkt durch die verschiedenen Formen der Differenzenquotienten ausgetauscht werden.

Eine Differenzengleichung ist eine numerisch lösbare rekursive Berechnungsvorschrift für eine diskret definierte Folge von nummerierten Folgeelementen bzw. Stützstellen $y_{k}$ im Abstand eines meist konstanten Intervalls Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta t} .

Siehe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \to} Regelungstechnik#Mathematische Methoden zur Beschreibung und Berechnung eines Regelkreises

Siehe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \to} Differenzengleichung (Differenzenverfahren)

Siehe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \to} Regelkreis#Simulation des Eingangs-Ausgangsverhaltens eines Regelkreises

Die folgenden Methoden, über das Frequenzverhalten die Stabilität der dynamischen Systeme zu bestimmen, dienen dem Verständnis, liefern aber keine Details zur Dynamik von Regelkreisen:

• Nyquistkriterium
• Komplexe Ebene
• Bode-Diagramm

Rückführung bei schaltgeregelten Systemen

Bei Ausstattung von überlagernd stetig wirkenden Rückführungen werden verschiedene Effekte erreicht.

• Schwingfrequenz vergrößern,
• Regelabweichung minimieren,
• Totzone und Hysterese festlegen.

Siehe Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \to} Regler#Unstetige Regler

Bedeutung in verschiedenen Bereichen

Elektrische Schaltungstechnik

Im Jahr 1912 patentierte Siegmund Strauss (* 1875, † 1942) eine Rückkopplungsschaltung mit einer Lieben-Röhre. Im Jahr 1913 entwickelten unabhängig voneinander Alexander Meißner (* 1883 in Wien, † 1958 in Berlin) bei Telefunken in Berlin und Edwin Howard Armstrong (* 1890, † 1954) in New York das System einer Sender- und Empfängerschaltung mittels Röhren-Verstärker mit Rückkopplung. Im Jahr 1914 patentierte Lee De Forest (* 1873, † 1961) seine Rückkopplungsschaltung. De Forest patentierte als Letzter, hatte aber wahrscheinlich die Rückkopplung als Erster im Labor festgestellt.

1927 entdeckte der Telefoningenieur Harold Stephen Black, dass man die Qualität eines Signalverstärkers erheblich verbessern kann, indem man einen Teil des Ausgangssignals vom Eingangssignal subtrahiert, was im Prinzip eine Gegenkopplung darstellt.

Weitere elektrotechnische Beispiele:

• überkritische positive Rückkopplung, auch Mitkopplung, von elektrischen Systemen zur Erzeugung von hoch- oder niederfrequenten Schwingungen. Sie findet Anwendung in Oszillatorschaltungen wie astabile Kippschaltungen und Funktionsgeneratoren.
• negative Rückkopplung, auch Gegenkopplung, von elektrischen Systemen zur Linearisierung des Frequenzganges sowie nichtlinearen Verzerrungen wie der Verringerung des Klirrfaktors. Bei zu großer Phasenverzögerung im Verstärker kann sich die negative Rückkopplung in eine positive Rückkopplung umwandeln und es entstehen unerwünschte Schwingungen.
• jeder Spannungsregler vergleicht die Ausgangsspannung mit einer Referenzspannung und regelt mit der verstärkten Differenzspannung die Stromdurchlässigkeit eines Leistungstransistors. Dadurch ist die Ausgangsspannung weitgehend unabhängig von Belastungsschwankungen.
• unterkritische positive Rückkopplung von Schwingkreisen zur Entdämpfung und damit Erhöhung des Resonanzwiderstandes. Anwendung fand diese Rückkopplung hauptsächlich bei der Audionschaltung. In dieser wurden durch Einsatz der Rückkopplung die Trennschärfe und die Empfindlichkeit des Empfängers erhöht, ohne die Anzahl der meist teuren Elektronenröhren im Empfangsgerät steigern zu müssen.

Tontechnik

→ Hauptartikel: Akustische Rückkopplung

In der Tontechnik bzw. der Elektroakustik ist Rückkopplung (kurz Kopplung oder „Koppeln“ oder „Feedback“ genannt) eine in aller Regel unerwünschte, als unangenehmes Pfeifen wahrgenommene Selbsterregung des Systems Schallaufnehmer – Verstärker – Lautsprecher. Hauptsächlich entsteht sie zwischen den vom Verstärker gespeisten Lautsprechern und den Mikrofonen. Aber auch jeder andere elektroakustische Schallaufnehmer, wie beispielsweise bei E-Gitarren oder Schallplattenspielern, kann betroffen sein. Eine Rückkopplung kann sich ausbilden, wenn ein Lautsprecher das Signal eines Mikrofons wiedergibt und gleichzeitig das Mikrofon dieses Signal erneut aufnimmt, wenn es zu nahe am Lautsprecher steht, wie es typischerweise etwa bei Hörgeräten vorkommt. Das Signal wird erneut verstärkt, über den Lautsprecher wiedergegeben und es entsteht eine elektroakustische Schleife, die sich bis zur Selbsterregung aufschaukelt. Die Frequenz der Selbsterregung hängt von den frequenzselektiven Eigenschaften und der Phasenverschiebung der Übertragungsstrecke (Luftstrecke, Equalizer, Lautsprecher, Mikrofoneigenschaften, reflektierende Raumwände) ab.

Im extremen Fall einer Rückkopplung ist neben der Belästigung der Zuhörer auch die Zerstörung der Lautsprecher möglich, insbesondere die Hochtöner können dadurch beschädigt werden. Tieftonlautsprecher und Subwoofer sind gegen Feedback unempfindlicher und verkraften auch ein stärkeres Feedback als Hochtöner. In Lautsprecherboxen befindliche Frequenzweichen können beschädigt werden.

Um Koppeln im Bühnenbetrieb zu vermeiden, können folgende Maßnahmen helfen:

• Equalizer, mit denen die Beschallungsanlage beim Soundcheck „eingepfiffen“ wird. Dabei wird absichtlich Feedback erzeugt, das von einem geschulten Techniker nach Gehör mit dem Equalizer minimiert oder beseitigt werden kann, indem diejenigen Frequenzen abgesenkt werden, die zum Koppeln neigen.
• So genannte Feedback-Destroyer (Rückkopplungsunterdrücker) erkennen und unterdrücken automatisch sich aufbauende Rückkopplungen. Das Problem dabei: Sie können nicht zwischen ungewollten und gewollten Rückkopplungen unterscheiden und unterdrücken beide gleichermaßen.
• Mikrofone und Lautsprecher können so aufgestellt werden, dass zwischen ihnen wenig Direktschall möglich ist;
• Der Einsatz von Mikrofonen mit einer geeigneten Richtcharakteristik („Niere“)
• Durch spezielle Anordnung und Verschaltung mehrerer Mikrofone kann die Auslöschung von Umgebungsschall bewirkt und so die Rückkopplungsgefahr verringert werden (siehe beispielsweise Grateful Dead);
• Der Verzicht auf Mikrofone durch Einsatz von Schwingungsaufnehmern oder elektrischen Instrumenten.
• Ist das Mikrofon nahe bei der Schallquelle, steigt der Pegel des Nutzsignales, nicht jedoch derjenige des Schalles vom Lautsprecher.
• Mit Optogates können unbenutzte Mikrofone automatisch abgeschaltet werden.

Oft tritt Kopplung bei leerem Zuhörersaal eher ein, als bei gefülltem, da die Zuhörer den Schall und dessen Reflexion im Raum dämpfen.

Das Feedback wird in verschiedenen modernen Musikstilen, vor allem aber in der Rockmusik, insbesondere beim Heavy Metal ganz bewusst als Sounddesign zur Klangbearbeitung eingesetzt.

Des Weiteren gibt es vereinzelt DJs, die Feedback in ihre Performance mit einbauen. Dazu wird das Signal am Kopfhörerausgang des Mischpults auf einen Eingang gelegt. Unter extrem vorsichtiger Verwendung der verschiedenen Regler (Höhen, Mitten, Tiefen usw.) können somit Geräusche von verzerrt über pfeifend bis hin zu rhythmisch schlagend und weiteren Variationen erzeugt werden. Jedes Mischpult reagiert auf diese Manipulation anders. Selbst bei geringen Veränderungen an den Reglern können schlagartig wechselnde Geräusche entstehen, die bei unvorsichtiger Handhabung, wie oben erwähnt, die Boxen zerstören können.

In der Computertechnik

In der Computertechnik kann Feedback dazu dienen, dem Nutzer Information über den aktuellen Zustand einer Anwendung zu geben. Dies kann mit optischen Mitteln geschehen, etwa durch farblich hervor gehobene Details in einer Graphischen Benutzeroberfläche. Oder es werden akustische Signale genutzt, indem ein Geräusch über einen Lautsprecher abgespielt wird. Manche Eingabegeräte besitzen die Fähigkeit, dem Nutzer mit mechanischen Mitteln eine Rückmeldung zu geben. Dieses Force-Feedback dient unter anderem, den Eindruck einer Simulation realistischer zu gestalten.

Die Hardware mancher Computerspiele ist in der Lage, dem Spieler mit mechanischen Mitteln Rückmeldungen über Ereignisse im Spiel zu geben. Dies wird häufig für eine direkte Reaktion auf Aktionen des Spielers genutzt. Ein Beispiel dafür sind Vibrationen eines Lenkrads.

Eine geschlossene Regelschleife mit dem Nutzer als Systemblock wird beim Verfahren User in the loop genutzt, um z. B. im Mobilfunk oder Smart Grid eine Nachfrageregelung zu erreichen.

System Erde und Klimaforschung

In der Klimatologie sind viele Rückkopplungen zu beobachten. Bei der Eis-Albedo-Rückkopplung (positive Rückkopplung) wird beispielsweise durch Vereisung mehr Sonnenlicht reflektiert, so dass es kälter wird. Damit können größere Flächen vereisen und es wird noch kälter. Umgekehrt funktioniert der Prozess ebenfalls.

Weitere Rückkopplungen beinhalten Wolken-Wasserdampf-Kopplungen („Der Wasserdampf-Effekt in der oberen Troposphäre ist der stärkste bekannte Rückkopplungsprozess.“) oder die Kohlendioxid-Aufnahmefähigkeit von Meeren. Viele dieser Prozesse sind noch nicht genau genug erforscht und erschweren eine genaue Klimavorhersage mit Klimamodellen. Dabei ist während der letzten 35 Jahren die Luftfeuchtigkeit am oberen Rand der Wetterschicht um durchschnittlich ca. zehn Prozent gestiegen.

Siehe auch: Folgen der globalen Erwärmung, Abschnitt Rückkopplungen und Folgen der globalen Erwärmung in der Arktis

Medizin und Biologie

In der Biologie und Medizin bewirkt negative Rückkopplung die Aufrechterhaltung der Homöostase (Gleichgewichtszustand innerhalb zulässiger Grenzen) eines Systems. Solche Regulationsvorgänge laufen z. B. beim Aufrechterhalten der Körpertemperatur von Warmblütern oder bei der Regulation der Genaktivität ab.

Dagegen bedeutet Biofeedback, dass z. B. ein Signalton oder eine Lampe eine Werteüberschreitung einer gemessenen Größe (z. B. Hauttemperatur, Muskelspannung/Tonus oder EEG-Wellenamplitude einer vorgewählten Frequenz) an die untersuchte Person zurückgemeldet wird, die ansonsten nicht oder nicht hinreichend wahrgenommen werden kann. Sie wird auf diese Weise erfahrbar gemacht und kann z. B. zum Erlernen einer Selbstkontrolle dienen.

Der menschliche Körper ist ein komplexes System, welches von einem sehr effektiven Feedback-Kontroll-System gesteuert und kontrolliert wird – dem Zentralnervensystem. Die aktuellen Sinneseindrücke werden dabei immer mit den dazu passenden Informationen (Erfahrungen) aus dem Gedächtnis kombiniert, um dem Individuum eine passende Zukunftsvorhersage als Handlungsvorschlag für die aktuelle Situation zu liefern. Damit kann man auf jede Situation sofort angemessen reagieren. Der Vorschlag des Gehirns wird immer an die aktuelle Situation angepasst. Z. B. steuert das Gehirn beim Gehen/Laufen nach der gesehenen optischen Information über die Beschaffenheit des Weges, wie man den Fuß aufsetzen muss. Das Feedback-System kann z. B. durch Drogen (Alkoholkonsum) gestört werden; dann torkelt man oder stürzt.

Siehe auch: Neurofeedback, Semantisches Feedback und Reafferenzprinzip

Psychologie

• In der allgemeinen Psychologie wird die unbewusste Wahrnehmung des eigenen Ausdrucksverhaltens (Körperhaltung, Gestik, Mimik) und deren Wirkung auf das eigene Wohlbefinden als Feedback bezeichnet. In einem Experiment von Strack u. a. (1988) wird beschrieben, dass die Bewertung des subjektiv empfundenen Witzes von Cartoons besser ausfällt, wenn die Probanden die für Freude typischen Gesichtsmuskeln aktivieren.
• In der Psychologie/Kommunikationstheorie hat Paul Watzlawick Rückkopplungsvorgänge thematisiert, indem er Kommunikationskreisläufe beschreibt, die keinen Anfang und kein Ende haben, also willkürlich „interpunktiert“ werden können. Er spricht dabei von „symmetrischer Eskalation“ bzw. von „Komplementarität“. Gemeint ist die gegenseitige Wechselwirkung der Verhaltensäußerungen von Kommunikationspartnern, die im einen Fall um dieselbe Position konkurrieren, im anderen Fall sich in ergänzenden Rollen gegenseitig bestärken bzw. festhalten.
• Ein ähnliches Konzept vertritt Walter Milowiz in der Systemtheorie, die er primär auf die Systemische Sozialarbeit anwendet. Hier werden Rückkopplungskreise und eskalierende Entwicklungen in der Interaktion zwischen Personen und ihrer Umgebung als Beschreibung für soziale Problemlagen wahrgenommen.

Siehe auch: Selbstregulation (Psychologie)

Siehe auch

• Pfadabhängigkeit
• Kybernetik
• Instrumentelle und operante Konditionierung

Wiktionary: Rückkopplung – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Literatur

• Siegfried Wirsum: Praktische Beschallungstechnik, Gerätekonzepte, Installation, Optimierung. 1. Auflage. Franzis-Verlag, München 1991, ISBN 3-7723-5862-4.
• Helmut Röder, Heinz Ruckriegel, Heinz Häberle: Elektronik 3.Teil, Nachrichtenelektronik. 5. Auflage. Verlag Europa-Lehrmittel, Wuppertal 1980, ISBN 3-8085-3225-4.
• Gustav Büscher, A. Wiegemann: Kleines ABC der Elektroakustik. 6. Auflage. Franzis Verlag, München 1972, ISBN 3-7723-0296-3.
• R. Beckmann: Handbuch der PA-Technik, Grundlagen-Komponenten-Praxis. 2. Auflage. Elektor-Verlag, Aachen 1990, ISBN 3-921608-66-X.
• I. Jöns, W. Bungard (Hrsg.): Feedbackinstrumente im Unternehmen – Grundlagen, Gestaltungshinweise, Erfahrungsberichte. Gabler, Wiesbaden 2005, ISBN 3-409-12738-0.
• Frank Pieper: Das P.A. Handbuch: Praktische Einführung in die professionelle Beschallungstechnik. 4. Auflage. GC Carstensen Verlag, München 2011, ISBN 978-3-910098-42-8.
• Frederic Vester: Die Kunst vernetzt zu denken. 8. Auflage. dtv, München 2011, ISBN 978-3-423-33077-0.
• Jürgen Beetz: Feedback: Wie Rückkopplung unser Leben bestimmt und Natur, Technik, Gesellschaft und Wirtschaft beherrscht. Springer Spektrum, Heidelberg 2015, ISBN 978-3-662-47089-3.