Apothema
aus Wikipedia, der freien Enzyklopädie
Dies ist die aktuelle Version dieser Seite, zuletzt bearbeitet am 7. Februar 2021 um 14:54 Uhr durch imported>Aka(568) (https, Kleinkram).
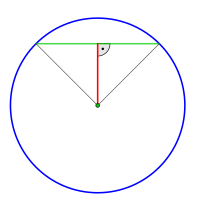
Das Apothema (altgriechisch ἀπόθεμα ‚Ablage‘) einer Kreissehne ist ihr Abstand vom Mittelpunkt des Kreises, also die Länge des Lotes vom Mittelpunkt auf die Sehne.[1]
Das Apothema eines regelmäßigen Vielecks[2] ist das Apothema seiner Kanten (als Sehnen im Umkreis) und gleichzeitig sein Inkreisradius.
Berechnung
Ist der Kreisradius und die Länge der Kreissehne, dann gilt nach dem Satz des Pythagoras für das Apothemas
und damit
- .
Das Apothema eines regelmäßigen n-Ecks der Kantenlänge ist
- .
Damit kann sein Flächeninhalt zu ermittelt werden. Für verschiedene ergeben sich die folgenden Werte:
| regelmäßiges Vieleck |
Seitenlänge | Apothema | Fläche |
|---|---|---|---|
| Dreieck | |||
| Viereck | |||
| Fünfeck | |||
| Sechseck | |||
| Achteck | |||
| -Eck | |||
| (Kreis) |
Siehe auch
Weblinks
Commons: Chord (geometry) – Sammlung von Bildern, Videos und Audiodateien
Wiktionary: Apothema – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen
- Eric W. Weisstein: Apothem. In: MathWorld (englisch).
- Sagitta, Apothem, and Chord Ed Pegg, Jr., The Wolfram Demonstrations Project
Einzelnachweise
- ↑ Paul Huther: Anfangsgründe der Geometrie vorzüglich zum Gebrauche an technischen Schulen. G. Joseph Manz, Regensburg 1838, eingeschränkte Vorschau in der Google-Buchsuche.
- ↑ J. Michael Köberlein: Lehrbuch der Elementar-Geometrie und Trigonometrie zunächst für Gymnasien und Lyzeen. J. E. von Seidel, Sulzbach 1824, eingeschränkte Vorschau in der Google-Buchsuche.