Kubische Iteration
Die kubische Iteration fällt in das Gebiet der diskreten Dynamiken in der komplexen Ebene.
Parameter für kubische Polynome
Jedes kubische Polynom ist unter einem komplexen, affinen Koordinatenwechsel äquivalent zu einem Polynom der Form
- .
Diese Normalform ist eindeutig bis auf den durch Multiplikation mit -1 gegebenen Koordinatenwechsel , der das Vorzeichen von umdreht. Die beiden Invarianten
beschreiben also vollständig die Äquivalenzklasse eines kubischen Polynoms bezüglich komplexer, affiner Koordinatenwechsel. Der Parameterraum kubischer Polynome ist also .
Julia-Mengen kubischer Polynome
Jedes Polynom definiert eine Abbildung der komplexen Ebene in sich selbst. Wählt man einen Startpunkt , so kann man verfolgen, wohin dieser durch transportiert wird. Wählt man rekursiv den jeweiligen Endpunkt als Anfangspunkt, so erhält man eine komplexwertige Folge , bei . In der üblichen Notation für mehrfache Verkettungen einer Abbildung mit sich gilt also .
Nach der allgemeinen Theorie der Iteration rationaler Funktionen kann man die Punkte der komplexen Ebene nun danach einteilen, ob die Folge für alle in einer kleinen Umgebung dasselbe Verhalten zeigt, diese bilden die Fatou-Menge der Iteration. Diejenigen Punkte , für die es in jeder kleinen Umgebung Punkte mit radikal abweichendem Verhalten der Folge gibt, bilden die Julia-Menge.
Ein kubisches Polynom hat zwei kritische Punkte, d. h. Nullstellen von . Es gibt die folgenden Möglichkeiten:
- Die Orbits beider kritischen Punkte gehen gegen Unendlich. Dann ist die Julia-Menge total unzusammenhängend.
- Der Orbit eines kritischen Punktes geht gegen Unendlich, während der Orbit des anderen kritischen Punktes beschränkt bleibt. Dann ist die Julia-Menge unzusammenhängend, aber im Allgemeinen nicht total unzusammenhängend.
- Beide kritische Punkte haben beschränkte Orbiten. Dann ist die Julia-Menge zusammenhängend.
Die kubische Mandelbrot-Menge
Die zum dritten Fall (zusammenhängende Julia-Menge) gehörenden Polynome beschreiben den Zusammenhangsort (engl. “connectedness locus”, nach Branner-Hubbard) oder die kubische Mandelbrot-Menge. Branner und Hubbard zeigen, dass diese Menge zellulär ist, d. h. der Durchschnitt einer absteigenden Folge 4-dimensionaler topologischer Kreisscheiben im Parameterraum . Insbesondere ist sie kompakt und zusammenhängend, und ihr Komplement ist ebenfalls zusammenhängend.
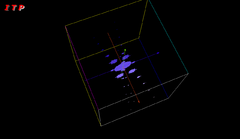
Visualisierung der kubischen Mandelbrotmenge
Die kubische Mandelbrotmenge kann man parametrisieren durch
- ,
sie hat dann eine vierzählige Symmetrie. Ein Spezialfall sind die Polynome . In diesem Fall erhält man als Mandelbrot-artige Menge den Kaktusfraktal.[1]
Problematisch bei der Visualisierung dieser Menge ist, dass der Parameterraum komplex zwei- und damit reell vierdimensional ist. Man hilft sich hier z. B., indem man einen der vier Parameter auswählt und ihn auf einen festen Wert setzt. Die anderen Parameter werden als Koordinaten in einem dreidimensionalen Raum verstanden. Man erhält einen dreidimensionalen Schnitt im vierdimensionalen Raum.
Um die vierte Dimension doch noch zu erfassen, kann diese als Zeit wieder eingeführt werden. D. h. man erzeugt Einzelbilder zu einer aufsteigenden Folge des vierten Parameters und fasst diese in einer Animation zusammen. Auf diese Weise erhält man einen Film, der eine Fahrt durch ein festgelegtes Intervall auf der „vierten Achse“ darstellt.
Die Menge hat eine fraktale Oberfläche und weist starke Parallelen mit der Mandelbrotmenge auf. Wenn man an den dreidimensionalen Objekten, die entstehen, wiederum zweidimensionale Schnitte ausführt, findet man in diesen Schnittebenen an manchen Stellen die charakteristische Form des Apfelmännchens wieder.
Literatur
- Bodil Branner, John H. Hubbard: The iteration of cubic polynomials Part I: The global topology of parameter space, Acta Mathematica, Band 160, 1988, S. 143–206, Online
- Bodil Branner, John H. Hubbard: The iteration of cubic polynomials Part II: patterns and parapatterns, Acta Mathematica, Band 169, 1992, S. 229–325, Project Euclid
- John Milnor: Remarks on iterated cubic maps, Experimental Mathematics, Band 1, 1992, S. 5–24, Project Euclid
Einzelnachweise
- ↑ Cactus Fractal (MathWorld)








![{\displaystyle p\in \mathbb {C} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ed93fc8cab2bdba4eb2b01cb946564e6d7b8c49)