Rechenseil
aus Wikipedia, der freien Enzyklopädie
Dies ist die aktuelle Version dieser Seite, zuletzt bearbeitet am 21. Januar 2022 um 09:39 Uhr durch imported>Anonym~dewiki(31560) (→Rechenfunktionen: Das Ergebnis von X Knoten minus Y Knoten muss Restzahl, nicht Gesamtzahl heißen. Das sagt die Logik!).
Das Rechenseil oder Knotenseil war ein gebräuchliches Rechenhilfsmittel des Mittelalters, mit dessen Hilfe man einfache numerische und geometrische Probleme lösen und demonstrieren konnte.
Als allegorische Personifizierung der Arithmetik bei der Darstellung der freien Künste diente eine weibliche Figur mit dem Attribut des Knotenseils. Als Knotenschnur findet das Symbol des Knotenseils Verwendung bei Freimaurern[1] und ähnlich auch in Pfadfinderkreisen.[2]
Ein Rechenseil hatte mehrere Knoten im Abstand einer Handbreite. Es wird oft fälschlich Zwölfknotenschnur[3][4][5] genannt. Eine Zwölfknotenschnur ist jedoch immer eine geschlossene (Ring-)Schnur. Mehr Knoten im Rechenseil waren speziell für die Multiplikation und Division von Vorteil.
Rechenfunktionen
| Arithmetik | |||
| Addition | X + Y = Z | Man zählt erst X Knoten ab, dann Y weitere. Die Gesamtzahl der abgezählten Knoten ist Z. | Bsp.: 5 + 4 = 9
|
| Subtraktion | X - Y = Z | Man zählt erst X Knoten ab und geht dann Y zurück. Die Restzahl der abgezählten Knoten ist Z. | Bsp.: 9 - 4 = 5
|
| Multiplikation | X × Y = Z | Man zählt X Knoten ab und legt diese Strecke Y mal zusammen. Die Gesamtzahl der abgezählten Knoten ist Z. | Bsp.: 4 * 3 = 12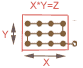
|
| Division | X / Y = Z (Rest Q) | Man zählt X Knoten ab. Davon nimmt man Y und legt diese so oft zusammen, bis alle aufgebraucht sind. Die Anzahl der Zusammenlegungen ist Z. Übrig gebliebene Knoten sind der Rest Q. | Bsp.: 13 / 4 = 3 Rest 1
|
| Geometrie | |||
| Rechter Winkel | 42 + 32 = 52 16 + 9 = 25 |
Man nagelt Anfang und Ende des Rechenseils zusammen. Für die Grundseite zählt man 5 ab (4 Teilstrecken) und nagelt dieses fest. Für die Senkrechte darauf benötigt man 4 Knoten (3 Teilstrecken). Durch das Spannen dieser Seiten entsteht ein rechtwinkliges Dreieck (Prinzip des Pythagoreischen Tripels). Fixiert man nun je 3 Teilstrecken der rechtwinkligen Seiten (7 Knoten) und zieht die restlichen 5 Knoten symmetrisch nach außen, entsteht ein Quadrat. | 
|
| Gleichseitiges Dreieck | Man nagelt Anfang und Ende des Rechenseils zusammen. Für die Grundseite zählt man 5 ab. Für die Seiten darauf benötigt man jeweils 5 Knoten. Durch das Spannen dieser Seiten entsteht ein gleichseitiges Dreieck. | 
| |
| Kreis, Sechseck | Man nagelt ein Ende fest und befestigt einen Griffel an der gewünschten Stelle. Dann führt man den Griffel am gespannten Seil einmal herum. Mit dem eingestellten Radius lässt sich der Kreisbogen leicht in ein Sechseck teilen. | ||
Einzelnachweise
- ↑ Timo Widmaier: Glossar der Freimaurerei: Kein Buch mit sieben Siegeln. In: Freimaurer. Logen, Meister, Rituale. Damals. Heft 5/2012, 19. April 2012 (auch Audio, MP3).
- ↑ Über das Symbol der Knotenschnur. In: knotenschnur.de. März 2021, abgerufen am 8. August 2021.
- ↑ Matthias Fürderer: Die Kulturgeschichte des Rechten Winkels. (PDF; 811 kB) (Nicht mehr online verfügbar.) Fachhochschule Nordwestschweiz, Pädagogische Hochschule, 4. April 2008, archiviert vom Original am 31. März 2010; abgerufen am 10. Oktober 2008.
- ↑ Walter Höhn: Das Geheimnis der Arbeitsmethodik mittelalterlicher Stadtplanungen. (Nicht mehr online verfügbar.) In: historisches-franken.de. Archiviert vom Original am 23. Oktober 2008; abgerufen am 10. Oktober 2008.
- ↑ Mathias Polster: Wie haben die das gemacht? Tipps von den mittelalterlichen Baustellen. (Nicht mehr online verfügbar.) In: Stadtschreiber: Geschichten aus der Stadt. stadtfuehrung-herford.de, 4. April 2008, archiviert vom Original am 23. Oktober 2008; abgerufen am 10. Oktober 2008.
Weblinks
- Gunter Krebs: Mathematik: Rechensseil (13-Knoten-Seil). Wissenschaft im Mittelalter. In: Turba Delirantium. 30. Januar 2005 (zuletzt abgerufen am 13. August 2021).
