Korrelationsungleichung

Als Korrelationsungleichungen werden eine Gruppe von mathematischen Ungleichungen bezeichnet, welche den Begriff der positiven Korrelation auf partiell geordnete Mengen (POSETs) und distributive Verbände übertragen. Sie haben darüber hinaus eine wahrscheinlichkeitstheoretische Interpretation und berühren das mathematische Teilgebiet der Theorie der stochastischen Ordnungen.

Die Entwicklung wurde angestoßen durch die FKG-Ungleichung aus dem Jahr 1971, benannt nach C. M. Fortuin, Jean Ginibre und P. W. Kasteleyn, welche auf verschiedensten Gebieten Anwendung gefunden hat, unter anderem auf den Gebieten statistische Mechanik, Partikelsysteme, Kombinatorik und Perkolationstheorie. Eine frühere Version dieser Ungleichung für unabhängige und identisch verteilte Zufallsvariablen wurde 1960 von Theodore Edward Harris bewiesen, wurde jedoch zunächst nicht von Mathematikern anderer Disziplinen rezipiert und erst durch die Veröffentlichung von Fortuin, Kasteleyn und Ginibre bekannt. In diesem Zusammenhang spielt der Begriff des assoziierten Maßes (auch Maß mit positiven Korrelationen) eine Rolle.

Ausgehend von der FKG-Ungleichungen wurden weitere ähnliche Ungleichungen gefunden, zum Beispiel die Holley-Ungleichung nach Richard Holley im Jahr 1974, oder die sehr allgemeine Vier-Funktionen-Ungleichung von Rudolf Ahlswede und David E. Daykin von 1978, aus der die anderen genannten Ungleichungen folgen.

Assoziierte Maße

Der Begriff des assoziierten Maßes wurde 1967 von J. D. Esary, Frank Proschan und D. W. Walkup eingeführt. Wegen der Analogie zu positiven Korrelationen von Zufallsvariablen wird von manchen Autoren auch die Bezeichnung Maß mit positiven Korrelationen verwendet.

Ein endliches Maß $\mu$ auf $(X,{\mathfrak {B}})$, wobei $X$ ein halbgeordneter topologischer Raum sei, heißt assoziiert, falls

$\int fg\;\mathrm {d} \mu \geq \int f\mathrm {d} \mu \cdot \int g\mathrm {d} \mu$

für alle beschränkten, stetigen, monoton wachsenden Funktionen $f,g$ von $X$ nach $\mathbb {R}$ gilt.

Die FKG-Ungleichung

Die FKG-Ungleichung, benannt nach C. M. Fortuin, J. Ginibre und P. W. Kasteleyn (1971), ist ursprünglich eine Korrelationsungleichung auf distributiven Verbänden. Sie ist ein fundamentales Werkzeug auf den Gebieten der statistischen Mechanik und der probabilistischen Kombinatorik (speziell auf dem Gebiet der Zufallsgraphen.) Sie besagt übertragen auf ein wahrscheinlichkeitstheoretisches Setting in etwa, dass wachsende Ereignisse miteinander positiv korreliert sind.

Formulierung für endliche distributive Verbände

Sei $X$ ein endlicher distributiver Verband, und $\mu$ ein Maß auf $X$, welches

$\mu (\{x\wedge y\})\mu (\{x\vee y\})\geq \mu (\{x\})\mu (\{y\})$

für alle $x$, $y$ im Verband $X$ erfüllt. Diese Eigenschaft heißt auch Log-Supermodularität.

Die FKG-Ungleichung besagt dann, dass das Maß $\mu$ assoziiert ist, also dass für zwei beliebige bezüglich der von den Verbandsoperationen induzierten Halbordnung stetige, monoton wachsende, quadratintegrierbare Funktionen $f$ und $g$ von $X$ nach $\mathbb {R}$ gilt, dass sie positiv korreliert sind:

$\int fg\;\mathrm {d} \mu \geq \int f\mathrm {d} \mu \cdot \int g\mathrm {d} \mu$.

Ebenfalls positiv korreliert sind zwei Funktionen $f$ und $g$, wenn man die Bedingung „monoton steigend“ durch „monoton fallend“ ersetzt. Ist die eine Funktion monoton wachsend, die andere monoton fallend, dann sind sie negativ korreliert. Ein Beweis befindet sich in der Originalarbeit.

Eine ähnliche Aussage gilt im allgemeineren Fall, dass Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X} ein abzählbarer kompakter metrischer Raum ist. In diesem Fall muss Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu} ein strikt positives endliches Maß sein und die Log-Supermodularität muss über Randereignisse (Zylindermengen) definiert werden.

Weitere Formulierungen

In Rinott, Saks findet sich der Beweis für eine Form der FKG-Ungleichung für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sigma} -finite Maße auf der (überabzählbaren) Menge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \R^d} . In diesem Fall wird Log-Supermodularität eines Maßes über die Dichtefunktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varphi} (bezüglich irgendeines Produktmaßes auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \R^d} ) definiert, welche für alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x,y \in \R^d} erfüllen muss:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varphi(x)\varphi(y) \le \varphi(x\wedge y) \varphi(x \vee y)} .

Die Griffith-Ungleichung ist eine weitere Ungleichung von 1967, welche die gleiche Aussage macht wie die FKG-Ungleichung, jedoch andere Voraussetzungen hat und Anwendung auf dem Gebiet des Ising-Modells hat.

Die Harris-Ungleichung

Die Harris-Ungleichung ist im Prinzip die FKG-Ungleichung für Produktmaße, benannt nach Theodore E. Harris, welcher sie 1960 beim Studium von Perkolationen in der Ebene gefunden hat.

Wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X} eine totalgeordnete Menge ist, dann ist die Log-Supermodularität automatisch für jedes Maß Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu} auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X} erfüllt.

Es gilt zum Beispiel, dass für jede Wahrscheinlichkeitsverteilung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu} auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbb R} , und monoton wachsende quadratintegrierbaren Funktionen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g}

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int_\R f(x)g(x) \,d\mu(x) \geq \int_\R f(x)\,d\mu(x) \, \int_\R g(x)\,d\mu(x),}

gilt. Dies folgt aus

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int_\R\int_\R [f(x)-f(y)][g(x)-g(y)]\,d\mu(x)\,d\mu(y) \geq 0}

(die Terme in den eckigen Klammern haben das jeweils gleiche Vorzeichen.)

Die Log-Supermodularität ist auch automatisch erfüllt, wenn der Verband ein Produkt totalgeordneter Verbände ist, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X=X_1\times\dots\times X_n} , und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu=\mu_1\otimes\dots\otimes\mu_n} ein Produktmaß auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X} . In der Anwendung ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu} häufig die (Produkt-)Verteilung von unabhängig und identisch verteilten Zufallsvariablen auf unabhängigen Kopien Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X_i} eines Wahrscheinlichkeitsraumes.

Sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle E} eine endliche Indexmenge. Sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X = \prod_{e\in E} \{0,1\}} versehen mit der koordinatenweisen Ordnung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \le} und mit den Verbands-Operationen:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \xi \vee \eta} sei für alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \xi, \eta \in X} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle e \in E} definiert über Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \xi(e) \vee \eta(e) := \max \{\xi(e), \eta(e)\}} ,

sowie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \xi \wedge \eta} entsprechend über Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \xi(e) \wedge \eta(e) := \min \{\xi(e), \eta(e)\}} .

Mit diesen Operationen ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X} eine Boolesche Algebra.

Sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu} ein Wahrscheinlichkeitsmaß auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (X, \wp(X))} . Dann schreibt sich die FKG-Ungleichung

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf E_\mu fg \ge (\mathbf E_\mu f )(\mathbf E_\mu g)}

für alle monoton wachsenden Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f,g} für die die Erwartungswerte existieren, wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf E_\mu} den Erwartungswert bezüglich Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu} bezeichne.

Ein Ereignis Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A \in \wp(X)} heißt entsprechend wachsend, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbb I_A(x) \le \mathbb I_A(y)} für alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x,y \in X} mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x \le y} . (Und ein Ereignis heißt fallend, wenn das Komplement Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Omega\setminus A} wachsend ist.)

Sind Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle B} wachsende Ereignisse, so gilt

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf P_{\mu}(A \cap B) \ge \mathbf P_{\mu}(A)\mathbf P_{\mu}(B).}

Ein Beweis der Harris-Ungleichung, der auf dem hier verwendeten Doppelintegral-Trick auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \{0,1\}} beruht, findet sich in Grimmett 1999.

Beispiele

Wabengitter mit zufällig eingefärbten Waben.

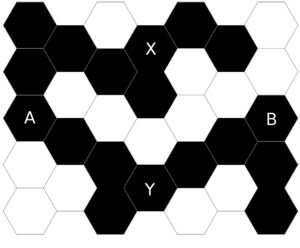
Man färbe zufällig jedes Hexagon des unendlichen Waben-Gitters schwarz jeweils stochastisch unabhängig voneinander mit Wahrscheinlichkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle p} und weiß mit Wahrscheinlichkeit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1-p} . Seien Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A, B, X, Y} vier (nicht notwendig verschiedene) solche Hexagone. Seien Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A \leftrightarrow B} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X\leftrightarrow Y} die Ereignisse, dass es einen schwarzen Pfad von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A} nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle B} respektive von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X} nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y} gibt. Dann besagt die FKG-Ungleichung, dass diese Ereignisse positive korreliert sind: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbf P(A \leftrightarrow B,\ X\leftrightarrow Y) \geq \mathbf P(A \leftrightarrow B)\mathbf P(X\leftrightarrow Y)} . In anderen Worten, wird vorausgesetzt, dass es bereits den einen schwarzen Pfad gibt, wird die Existenz des anderen Pfades wahrscheinlicher.

Im Erdős-Rényi-Zufallsgraph ist die Existenz eines Hamilton-Zyklus negativ korreliert mit der 3-Färbbarkeit des Graphen, da die Wahrscheinlichkeit der Existenz eines Hamilton-Zyklus mit der Anzahl der belegten Verbindungen steigt (steigendes Ereignis), während die Wahrscheinlichkeit von letzterem fällt (fallendes Ereignis).

Die Holley-Ungleichung

Diese von Richard Holley 1974 entdeckte und gelegentlich als Holley-Ungleichung bezeichnete Ungleichung besagt: Seien Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_1} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_2} zwei strikt positive Verteilungen auf einem endlichen distributiven Verband Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X} , welche

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_1(\{x\wedge y\})\mu_2(\{x\vee y\}) \ge \mu_1(\{x\})\mu_2(y\})} für alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x, y \in X}

erfüllen. Dann gilt

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int f \;\mathrm d\mu_2 \ge \int f\; \mathrm d\mu_1} .

für alle monoton wachsende integrierbaren Funktionen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f} auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X} . Dies ist gleichbedeutend damit, dass Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_2} größer als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_1} bezüglich der gewöhnlichen stochastischen Ordnung ist. Thomas Liggett hat einen Beweis für Räume der Form Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Omega = \prod_{s\in S} \{0,1\}} , welcher auf der Kopplung zweier Markow-Ketten in stetiger Zeit mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_1} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu_2} als stationären Verteilungen beruht. Er gibt darüber hinaus an, wie der Beweis auf abzählbare Produkträume zu erweitern wäre. Aus der Holley-Ungleichung lässt sich die FKG-Ungleichung durch geschicktes Einsetzen folgern.

Alternative Voraussetzung für die FKG-Ungleichung

Sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbb R^d} versehen mit der koordinatenweisen Halbordnung. Für eine Verteilung Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu} auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbb R^d} ist folgende Eigenschaft oft leichter zu überprüfen als die Log-Supermodularität:

Fixiert man eine Koordinate Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle i \in \{1, \dots, d\}} und zwei Konfigurationen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varphi} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \psi} in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mathbb R^d} bezüglich der anderen Koordinaten, so dass Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varphi_j \geq \psi_j} for all Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle w\not=v} , die auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu} bedingte Verteilung von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varphi_i} gegeben Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \{\varphi(j) : j\not=i\}} ist stochastisch größer als die auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu} bedingte Verteilung von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \psi} gegeben Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \{\psi_j: j\not=i\}} .

Erfüllt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu} diese Eigenschaft, dann ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu} assoziiert.

Die Vier-Funktionen-Ungleichung

Die Vier-Funktionen-Ungleichung von Ahlswede and Daykin von 1978 lässt sich wie folgt formulieren: Seien Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_1, f_2, g_1, g_2} nichtnegative reellwertige Funktionen auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \R^d} , welche folgende Bedingung erfüllen:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_1(x)f_2(y) \le g_1(x\vee y)g_2(x\wedge y) } für alle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x,y}

Dann gilt für jedes log-supermodulare Maß Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \mu} auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \R^d} ,

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \int_{\R^d} f_1(x)\mathrm d\mu(x) \int_{\R^d} f_2(x)\mathrm d\mu(x) \le \int_{\R^d} g_1(x)\mathrm d\mu(x) \int_{\R^d} g_2(x)\mathrm d\mu(x) }

Es lässt sich zeigen, dass aus der Vier-Funktionen-Ungleichung Holleys Ungleichung folgt, aus der wiederum die FKG-Ungleichung folgt.

Literatur

• C. M. Fortuin, P.W. Kasteleyn, J. Ginibre: Correlation inequalities on some partially ordered sets. In: Comm. Math. Phys. Nr. 22, 1971, MR0309498, ISSN 0010-3616, S. 89–103.
• P.C. Fishburn: FKG inequality. In: Michiel Hazewinkel (Hrsg.): Encyclopaedia of Mathematics, Kluwer Academic Publishers, 2001, ISBN 978-1-55608-010-4.
• P.C. Fishburn: Correlation inequalities. In: Michiel Hazewinkel (Hrsg.): Encyclopaedia of Mathematics, Kluwer Academic Publishers, 2001, ISBN 978-1-55608-010-4.
• H.-O. Georgii, O. Haggstrom, C. Maes: The random geometry of equilibrium phases. In: Phase transitions and critical phenomena. Nr. 18, 2001, Academic Press, San Diego, CA, MR2014387, S. 1–142.
• G. R. Grimmett: Percolation. Second edition. Springer-Verlag, New York 1999, MR1707339, ISBN 3-540-64902-6.
• T. E. Harris: A lower bound for the critical probability in a certain percolation. In: Proceedings of the Cambridge Philosophical Society, Nr. 56, 1960, MR0115221, S. 13–20.
• R. Holley: Remarks on the FKG inequalities. In: Communications in Mathematical Physics Nr. 36, 1974, MR0341552, ISSN 0010-3616, S. 227–231.
• Thomas M. Liggett: Interacting Particle Systems. Springer-Verlag, New York, 1985. ISBN 3-540-96069-4.
• R. Lyons: Phase transitions on nonamenable graphs In: J. Math. Phys. Nr. 41, 2000, MR1757952, S. 1099–1126.
• S. Sheffield: Random surfaces. In: Asterisque, Nr. 304, 2005, MR2251117.
• A. Müller and D. Stoyan: Comparison Methods for Stochastic Models and Risk. Wiley, Chichester, 2002.
• Yosef Rinott, Michael Saks: On FKG-type and permanental inequalities. In: Moshe Shaked, Y. L. Tong (Hrsg.): Stochastic inequalities: Papers from the AMS-IMS-SIAM Joint Summer Research Conference held in Seattle, Washington. July 1991 (Hayward, CA: Institute of Mathematical Statistics, 1992), ISBN 0-940600-29-3, ISBN 978-0-940600-29-4, 332–342, MR1228073.