Satz von Cantor-Bernstein-Schröder

Der Satz von Cantor-Bernstein-Schröder oder kurz Äquivalenzsatz ist ein Satz der Mengenlehre über die Mächtigkeiten zweier Mengen. Er ist nach den Mathematikern Georg Cantor (der ihn als erster formuliert hat), Felix Bernstein sowie Ernst Schröder (die Beweise veröffentlichten) benannt und wird in der Literatur auch als Cantor-Bernstein-Schröderscher [Äquivalenz-]Satz, Satz von Cantor-Bernstein, Äquivalenzsatz von Cantor-Bernstein, Satz von Schröder-Bernstein oder ähnlich bezeichnet. Allerdings wurde er unabhängig auch von Richard Dedekind bewiesen.

Der Satz besagt: Ist eine Menge A gleichmächtig zu einer Teilmenge einer zweiten Menge B und ist diese zweite Menge B gleichmächtig zu einer Teilmenge der ersten Menge A, so sind A und B gleichmächtig.

Der Satz von Cantor-Bernstein-Schröder ist ein wichtiges Hilfsmittel beim Nachweis der Gleichmächtigkeit zweier Mengen.

Geschichte

Der Äquivalenzsatz wurde 1887 von Georg Cantor formuliert, aber erst 1897 vom 19-jährigen Felix Bernstein in einem von Georg Cantor geleiteten Seminar und etwa gleichzeitig unabhängig von Ernst Schröder bewiesen. Cantor teilte Bernsteins Beweis noch im gleichen Jahr Émile Borel auf dem ersten internationalen Mathematiker-Kongress in Zürich mit.

Cantors erste Erwähnung des Äquivalenzsatzes, 1887

Cantor hatte diesen Äquivalenzsatz erstmals in seiner philosophischen Abhandlung Mitteilungen zur Lehre vom Transfiniten aus dem Jahre 1887 (ohne Beweis) mitgeteilt. In seiner großen Arbeit Beiträge zur Begründung der transfiniten Mengenlehre von 1895 hat Cantor diesen Satz erneut aufgestellt und aus dem Vergleichbarkeitssatz für Kardinalzahlen gefolgert. Den Vergleichbarkeitssatz konnte Cantor jedoch nicht beweisen. Er ist nach Friedrich Moritz Hartogs (Über das Problem der Wohlordnung, 1915) mit dem Auswahlaxiom (bzw. Auswahlprinzip oder Wohlordnungssatz) äquivalent.

Dedekind selbst fand den Beweis des Äquivalenzsatzes (welcher sich in seinem Nachlass fand) bereits am 11. Juli 1887, jedoch publizierte er ihn nicht und teilte ihn auch nicht Cantor mit.
Ernst Zermelo entdeckte Dedekinds Beweis wieder und gab 1908 in seiner Abhandlung Untersuchungen über die Grundlagen der Mengenlehre I einen Beweis, wobei er auf die Dedekindsche Kettentheorie aus Dedekinds Schrift Was sind und was sollen die Zahlen? (1888) zurückgriff. Giuseppe Peano gab einen ähnlichen Beweis, wobei es zu einem Prioritätsstreit mit Zermelo kam. Beide Beweise waren die Folge einer Herausforderung von Henri Poincaré, der um 1905 nach Beweisen verlangte, die ohne vollständige Induktion auskommen. Aufgrund von Poincarés Herausforderung wurde auch der Beweis von Julius König publiziert und weitere Forschung angeregt.

Ernst Schröder hatte 1896 (Ueber zwei Definitionen der Endlichkeit und G. Cantor’sche Sätze) eine Beweisskizze publiziert, die sich allerdings als falsch herausstellte, wie Alwin Reinhold Korselt 1911 (Über einen Beweis des Äquivalenzsatzes) bemerkt hatte; Schröder hat dort den Fehler in seinem Beweis bestätigt.

Dass der Satz auch ohne Auswahlaxiom beweisbar ist, haben Richard Dedekind 1887 und Bernstein 1898 in seiner Dissertation gezeigt (Bernsteins Beweis erschien zuerst in Borels Leçons sur la théorie des fonctions und dann nochmals in Bernsteins Abhandlung Untersuchungen aus der Mengenlehre).

Es gibt noch zahlreiche weitere Beweise des Satzes.

Eine passende Bezeichnung für den Äquivalenzsatz wäre Cantor-Dedekindscher Äquivalenzsatz oder Cantor-Dedekind-Bernsteinscher Äquivalenzsatz. Zudem hat Bernstein darauf hingewiesen, dass Cantor selbst die Bezeichnung „Äquivalenzsatz“ vorgeschlagen habe.

Satz

Das Cantor-Bernstein-Schröder-Theorem lautet:

Sei eine Menge $A$ gleichmächtig zu einer Teilmenge einer Menge $B$, und sei $B$ gleichmächtig zu einer Teilmenge von $A$. Dann sind $A$ und $B$ gleichmächtig.

Dabei heißen zwei Mengen gleichmächtig, wenn es eine bijektive Abbildung zwischen ihnen gibt. Ausgedrückt durch die Mächtigkeiten von $A$ und $B$ lautet das Theorem:

Aus $|A|\leqq |B|$ und $|B|\leqq |A|$ folgt $|A|=|B|$.

Dabei gilt $|A|=|B|$ genau dann, wenn $A$ und $B$ gleichmächtig sind, und $|A|\leqq |B|$ gilt genau dann, wenn $A$ gleichmächtig zu einer Teilmenge von $B$ ist, das heißt, wenn es eine injektive Abbildung von $A$ in $B$ gibt. Ausgedrückt durch die Eigenschaften von Funktionen lautet das Theorem:

Seien $A$ und $B$ Mengen mit einer Injektion $f\colon A\to B$ und einer Injektion $g\colon B\to A$. Dann existiert eine Bijektion $h\colon A\to B$.

Beweisidee

Im Folgenden ist hier eine Beweisidee gegeben.

Definiere die Mengen:

$C_{0}:=A\setminus g(B)$,

$C_{n+1}:=g(f(C_{n}))\quad {\mbox{ für }}n\geqq 0$,

$C:=\bigcup _{n=0}^{\infty }C_{n}$.

Für jedes $x$ aus $A$ setze dann:

$h(x):={\begin{cases}f(x),&\mathrm {falls} \ x\in C,\\g^{-1}(x),&\mathrm {falls} \ x\notin C.\end{cases}}$

Da im Falle, dass $x$ nicht in $C$ ist, $x$ in $g(B)$ liegen muss, gibt es ein eindeutig bestimmtes Element $g^{-1}(x)$ und $h$ ist eine wohldefinierte Abbildung von $A$ nach $B$.

Man kann nun zeigen, dass diese Funktion $h\colon A\to B$ die gewünschte Bijektion ist.

Beachte, dass diese Definition von $h$ nicht konstruktiv ist, d. h., es gibt kein Verfahren, um für beliebige Mengen $A$, $B$ und Injektionen $f$, $g$ in endlich vielen Schritten zu entscheiden, ob ein $x$ aus $A$ in $C$ liegt oder nicht. Für spezielle Mengen und Abbildungen kann das natürlich möglich sein.

Ein kurzer und leicht verständlicher Beweis findet sich auch in dem Göschen-Bändchen Mengenlehre Erich Kamkes.

Veranschaulichung

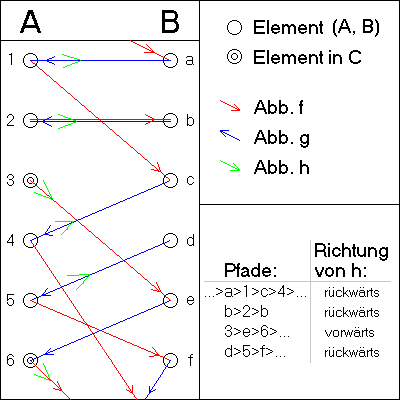
Veranschaulichen kann man sich die Definition von $h$ anhand der nebenstehenden Darstellung.

Dargestellt sind Teile der (disjunkten) Mengen $A$ und $B$ sowie die Abbildungen $f$ und $g$. Betrachtet man $A$ vereinigt $B$ als Graphen, dann zerfällt der Graph in verschiedene Zusammenhangskomponenten. Diese lassen sich in vier Typen einteilen:

1. beidseitig unendliche Pfade;
2. endliche Zyklen;
3. unendliche Pfade, die in $A$ beginnen;
4. unendliche Pfade, die in $B$ beginnen

(von jedem Typ ist hier einer vertreten, da der Pfad durch das Element $a$ beidseitig unendlich sein soll). Es ist aber allgemein nicht in endlich vielen Schritten entscheidbar, welchen Typ der durch ein vorgegebenes Element gehende Pfad hat.

Die im Abschnitt Beweisidee definierte Menge $C$ enthält nun genau die Elemente von $A$, die Teil eines in $A$ beginnenden Pfades sind. Die Abbildung $h$ wird so definiert, dass sie innerhalb einer jeden Zusammenhangskomponente eine Bijektion der $A$-Elemente auf „im Pfad benachbarte“ $B$-Elemente herstellt (dabei hat man bei den beidseitig unendlichen Pfaden und den endlichen Zyklen eine Richtungswahl und man legt sich auf „rückwärts“ fest).

Verallgemeinerung

Das Cantor-Bernstein-Schröder-Theorem erweist sich als direkte Folge des banachschen Abbildungssatzes.

Siehe auch

• Vergleichbarkeitssatz

Literatur

• Felix Bernstein: Untersuchungen aus der Mengenlehre. Buchdruckerei des Waisenhauses, Halle a. S. 1901 (Internet Archive – Inaugural-Dissertation bei David Hilbert). 
  • Felix Bernstein: Untersuchungen aus der Mengenlehre. In: Felix Klein, Walther von Dyck, David Hilbert (Hrsg.): Mathematische Annalen. Band 61, Nr. 1. B. G. Teubner, 1905, ISSN 0025-5831, S. 117–155, doi:10.1007/BF01457734 (gdz.sub.uni-goettingen.de [PDF] unveränderte Auflage bis auf einige Verbesserungen sowie Bemerkungen). 
• Émile Borel: Leçons sur la théorie des fonctions. Gauthier-Villars et fils, Paris 1898, S. 103 ff. (Textarchiv – Internet Archive). 
• Günter Bruns, Jürgen Schmidt: Eine Verschärfung des Bernsteinschen Äquivalenzsatzes. In: Heinrich Behnke, Richard Courant, Heinz Hopf, Gottfried Köthe, Kurt Reidemeister, Bartel L. van der Waerden (Hrsg.): Mathematische Annalen. Band 135, Nr. 3. Springer-Verlag, 1958, ISSN 0025-5831, S. 257–262, doi:10.1007/BF01351802 (gdz.sub.uni-goettingen.de [PDF] eingegangen am 3. Januar 1958). 
• Georg Cantor: Grundlagen einer allgemeinen Mannichfaltigkeitslehre. Ein mathematisch-philosophischer Versuch in der Lehre des Unendlichen. Commissions-Verlag von B. G. Teubner, Leipzig 1883 (digital.slub-dresden.de [PDF]). 
  • Georg Cantor: Ueber unendliche, lineare Punktmannichfaltigkeiten. 5. In: Felix Klein, Adolph Mayer (Hrsg.): Math. Ann. Band 21, Nr. 4. B. G. Teubner, 1883, ISSN 0025-5831, S. 545–591, doi:10.1007/BF01446819 (gdz.sub.uni-goettingen.de [PDF] Nachdruck; Halle, Oktober 1882). 
• Georg Cantor: Gesammelte Abhandlungen mathematischen und philosophischen Inhalts. Mit erläuternden Anmerkungen sowie mit Ergänzungen aus dem Briefwechsel Cantor–Dedekind. Hrsg.: Adolf Fraenkel (Lebenslauf); Ernst Zermelo. Verlag von Julius Springer, Berlin 1932 (gdz.sub.uni-goettingen.de). 
• Richard Dedekind: Was sind und was sollen die Zahlen? 2., unveränderte Auflage. Friedrich Vieweg & Sohn, Braunschweig 1893 (echo.mpiwg-berlin.mpg.de – Erstausgabe: 1888). 
• Richard Dedekind: Gesammelte mathematische Werke. Hrsg.: Robert Fricke, Emmy Noether, Øystein Ore. Band 3. Friedr. Vieweg & Sohn, Braunschweig 1932 (gdz.sub.uni-goettingen.de). 
• Friedrich Moritz Hartogs: Über das Problem der Wohlordnung. In: Felix Klein, Walther von Dyck, David Hilbert, Otto Blumenthal (Hrsg.): Math. Ann. Band 76, Nr. 4. B. G. Teubner, 1915, ISSN 0025-5831, S. 438–443, doi:10.1007/BF01458215 (gdz.sub.uni-goettingen.de [PDF] Juli 1914). 
• Alwin Reinhold Korselt: Über einen Beweis des Äquivalenzsatzes. In: Felix Klein, Walther von Dyck, David Hilbert, Otto Blumenthal (Hrsg.): Math. Ann. Band 70, Nr. 2. B. G. Teubner, 1911, ISSN 0025-5831, S. 294–296, doi:10.1007/BF01461161 (gdz.sub.uni-goettingen.de [PDF] Ende April 1910). 
• Ernst Schröder: Ueber zwei Definitionen der Endlichkeit und G. Cantor’sche Sätze. In: Kaiserliche Leopoldino-Carolinische Deutsche Akademie der Naturforscher (Hrsg.): Nova Acta, Abhandlungen der Kaiserl. Leop.-Carol. Deutschen Akademie der Naturforscher. Band 71, Nr. 6. Johann Ambrosius Barth Verlag, Halle a. S. 1898, S. 303–376 (biodiversitylibrary.org – Februar 1896, eingegangen am 21. Mai 1896). 
• Ernst Zermelo: Untersuchungen über die Grundlagen der Mengenlehre. I. In: Felix Klein, Walther von Dyck, David Hilbert, Otto Blumenthal (Hrsg.): Math. Ann. Band 65, Nr. 2. B. G. Teubner, 1908, ISSN 0025-5831, S. 261–281, doi:10.1007/BF01449999 (gdz.sub.uni-goettingen.de [PDF] 30. Juli 1907). 
• Arie Hinkis: Proofs of the Cantor-Bernstein theorem, a mathematical excursion. Birkhäuser 2013.

Weblinks

• Martin_Infinite: Der Satz von Schröder-Bernstein ‒ Explizit. Matroids Matheplanet, 19. November 2005, abgerufen am 13. September 2021.