Impedanzanpassung

In der Hochfrequenztechnik versteht man unter Impedanzanpassung (englisch Impedance matching) den Entwurf oder Abgleich passender Eingangsimpedanz einer Last zur Ausgangsimpedanz der Quelle in einem Stromkreis zum optimalen Erreichen eines gewünschten Zieles. Dabei sind Impedanzen im Allgemeinen komplex. Häufig wird die Auswahl entweder bestimmt durch das Ziel maximaler Wirkleistungsübertragung von der Quelle zur Last (Leistungsanpassung mit s), oder aber durch das Ziel minimaler Reflexionen auf einer Leitung (Leitungsanpassung ohne s). Eine typische Anwendung der Impedanzanpassung, ist z. B. die verbesserte Leistungsübertragung von einem Radiosender über die Leitung zur Antenne. Eine Signalübertragung ohne störende Reflexionen auf einer Leitung ist eine andere Anwendung. Sie lässt sich nach entsprechend anderen Gesichtspunkten ebenfalls durch Impedanzanpassung erreichen. Es kann auch auf beides ankommen. Um Mehrdeutigkeit zu vermeiden, sollte man dem Begriff Impedanzanpassung das jeweils angestrebte Ziel hinzufügen.

Wird ein Anpassungsziel nicht perfekt erreicht, spricht man bezüglich des angestrebten Optimums von Fehlanpassung. Fast nie lassen sich alle wünschenswerten Anpassungsziele gleichzeitig erreichen. Dann ist ein guter Kompromiss das Ziel. So kann z. B. eine suboptimale Anpassung auf einer Frequenz zugunsten verbesserter Anpassung auf dem gesamten benötigten Frequenzbereich (Bandbreite) in Kauf genommen werden.

Weitere Ziele sind z. B. ein guter Wirkungsgrad der Energiequelle (durch Spannungsanpassung) oder bestmögliches Signal-Rausch-Verhältnis am Ausgang eines Eingangsverstärkers.

In der Audiotechnik der Unterhaltungsindustrie ist die Spannungsanpassung die übliche Anpassung. Diese erlaubt das Parallelschalten mehrerer Verbraucher an eine Quelle. Auch die Energietechnik arbeitet mit Spannungsanpassung; hier steht maximaler Wirkungsgrad im Vordergrund.

Ursache

Oftmals ist eine Lastimpedanz nicht an eine Leitung angepasst, was bei Wechselströmen der Radio- und Hochfrequenztechnik zu stehenden Wellen auf der Leitung führt, wodurch nicht die vollständige Leistung vom Generator zur Last übertragen werden kann. Auf einer Leitung mit vollständig stehender Welle kann keine Energie transportiert werden. Dieser Effekt kann mit Stichleitungen oder durch Parallel- bzw. Serienschaltung von Kapazität(en) oder Induktivität(en) verhindert werden. Solche Impedanzwandler passen die Quellimpedanz oder eine Leitung an die Lastimpedanz an.

Um die optimale Anpassstruktur sowie Bauteilegrößen zu bestimmen, wird die Anpassung mit Hilfe des Smith-Diagramms simuliert; siehe auch Resonanztransformator und Leitungstransformation.

Anpassstrukturen

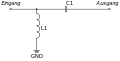
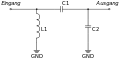
In der Praxis gibt es Anpassstrukturen, mit deren Hilfe man jede Impedanz an den Wellenwiderstand der Leitung anpassen kann: L-, T- sowie Pi- bzw. $\pi$-Struktur. Der Name wird vom Aussehen der Bauteilanordnung abgeleitet. Dabei kann in jedem Zweig eine Spule oder Kondensator liegen, die unten aufgeführten Bestückungen sind nur beispielhaft. Die Auswahl der Anpassstruktur ist nicht nur vom notwendigen Transformationsweg und somit der Anpassung abhängig, sondern auch von den peripheren Umgebungsbedingungen.

• Anpassstrukturen
• 

  T-Anpassstruktur

• 

  L-Anpassstruktur

• 

  Pi-Anpassstruktur

Beim Aufbau muss besonders auf eine auf die HF-Leitung eingekoppelte Versorgungsspannung also eine Spannungsquelle (Gleichspannung) geachtet werden, wodurch z. B. ein direkter Anschluss einer Spule auf Masse nicht möglich ist. Die Gleichspannung muss daher durch einen in Serie geschalteten Kondensator blockiert werden. Je größer dessen Kapazität ist, desto weniger beeinflusst er die Impedanz des mit der Betriebsspannung versorgten Bauteils.

L-Anpassstruktur

Unter Anpassnetzwerken ist eines der beliebtesten Entwurfsmethoden das verlustfreie L-Netzwerk. Dieses gilt für reelle Impedanzanpassungen.

Hat eine Impedanz auch einen imaginären Anteil, wie Spule oder Kondensator, muss als erstes konjugiert komplex erweitert werden, um den imaginären Anteil zu kompensieren. Hat eine Kapazität einen imaginären Blindwiderstand von −50 Ω, muss sie mit einer Spule, die eine Impedanz von +50 Ω aufweist, mittels Reihenschaltung kompensiert werden.

Schema Impedanzanpassung

Für die Dimensionierung ist das Parallelelement $X_{\text{p}}$ parallel zum größeren Widerstand, mit $R_{\text{q}}$ als Quellenwiderstand und $R_{\text{l}}$ als Lastwiderstand

$Z_{\text{links}}=R_{\text{links}}+\mathrm {j} X_{\text{links}}={\frac {R_{\text{q}}X_{\text{p}}^{2}+\mathrm {j} R_{\text{q}}^{2}X_{\text{p}}}{R_{\text{q}}^{2}+X_{\text{p}}^{2}}}$

daraus folgen zwei Gleichungen:

$R_{\text{links}}=R_{\text{l}}={\frac {R_{\text{q}}X_{\text{p}}^{2}}{R_{\text{q}}^{2}+X_{\text{p}}^{2}}}$

$X_{\text{links}}=-X_{\text{l}}=\mathrm {j} {\frac {R_{\text{q}}^{2}X_{\text{p}}}{R_{\text{q}}^{2}+X_{\text{p}}^{2}}}$

Als Erstes wird $X_{\text{p}}$ berechnet aus $R_{\text{l}}$ und $R_{\text{q}}$. $X_{\text{p}}$ kann der Blindwiderstand eines Kondensators oder eine Spule sein. Der resultierende Blindwiderstand in $X_{\text{links}}$ muss nun nur noch mit dem konjugiert komplexen Element $X_{\text{s}}$ kompensiert werden.

Mikrostreifen-Anpassung

Für die höheren Frequenzbereiche ab 1 GHz haben Leitungslängen immer größere Einflüsse. Diese kann man auch ausnutzen, um Impedanzen anzupassen. Es gibt offene Stichleitungen und kurzgeschlossene Stichleitungen, welche Impedanzen anpassen.

Ein bestimmter Abstand von der kleineren Impedanz weg „$d$“ wird so gewählt, dass für die Eingangsimpedanz $Z$ oder Admittanz $Y$ der Realteil angepasst ist.

Die Länge „$l$“ der Stichleitung wird so gewählt, dass der Blindanteil der Eingangsimpedanz $Z$ oder Admittanz $Y$ kompensiert und null wird.

Siehe auch

• Impedanzwandler
• Fehlanpassung
• s-Parameter

Literatur

• Thomas H. Lee, Planar Microwave Engineering, Cambridge, University Press, 2004, ISBN 978-0-521-83526-8.