Der Beweis der Potenzregel
Wir wollen vier Aussagen zeigen:
- A: Die Funktion
 hat an der Stelle
hat an der Stelle  eine Steigung von 2.
eine Steigung von 2.
- B: Die Funktion
 hat an der Stelle
hat an der Stelle  eine Steigung von
eine Steigung von  .
.
- C: Die Funktion
 hat an der Stelle
hat an der Stelle  eine Steigung von n.
eine Steigung von n.
- D: Die Funktion
 hat an der Stelle
hat an der Stelle  eine Steigung von
eine Steigung von  .
.
Frage: Dabei sind doch B und C eine Verallgemeinerung von A (mit einem Parameter  bzw.
bzw.  ), und D ist eine Verallgemeinerung von allen (mit beiden Parametern gleichzeitig). Würde es nicht reichen, nur D zu zeigen ?
), und D ist eine Verallgemeinerung von allen (mit beiden Parametern gleichzeitig). Würde es nicht reichen, nur D zu zeigen ?
Antwort: Ja. Allerdings ist der Beweis von D kompliziert, weil die vielen  und
und  das Gehirn verwirren und vom Wesentlichen ablenken. Daher bitte mit A beginnen. Es ist mir lieber, Sie haben Teil A wirklich verstanden, als dass Sie gleich mit Teil D beginnen, sich davon verwirren lassen und abschalten.
das Gehirn verwirren und vom Wesentlichen ablenken. Daher bitte mit A beginnen. Es ist mir lieber, Sie haben Teil A wirklich verstanden, als dass Sie gleich mit Teil D beginnen, sich davon verwirren lassen und abschalten.
Frage: Warum steht da oben in A  und nicht
und nicht  ?
?
Antwort für Anfänger: Das hat nichts zu bedeuten, wenn Sie in einer Gleichung von der kleinen Null verwirrt werden, dann lassen Sie die einfach weg, die Gleichung gilt dann immer noch.
Antwort für Fortgeschrittene: Wir betrachten eine Funktion, und der streng geschützte Markenname  bleibt reserviert für die allgemeine Variable dieser Funktion. Für ein bestimmtes festes
bleibt reserviert für die allgemeine Variable dieser Funktion. Für ein bestimmtes festes  bleibt dann nur noch der zugegebenermaßen etwas blödere Name
bleibt dann nur noch der zugegebenermaßen etwas blödere Name  übrig. Wenn wir sagen würden „
übrig. Wenn wir sagen würden „ ist jetzt mal immer 1“, dann wird die Funktion zu einem Punkt, und es gibt gar keine Steigung mehr.
ist jetzt mal immer 1“, dann wird die Funktion zu einem Punkt, und es gibt gar keine Steigung mehr.
Frage: Warum gibt es einen Anhang zu den Binomischen Formeln ?
Antwort: Jeder kennt  , aber was ist
, aber was ist  oder gar
oder gar  ? Um den Beweis einfacher zu machen, wird auf den Anhang verwiesen.
? Um den Beweis einfacher zu machen, wird auf den Anhang verwiesen.
Frage: Wie berechne ich eine Sekantensteigung ?
Antwort: Wie bei jeder anderen Linearen Funktion, siehe auch:
Frage: Ich verstehe das mit den vielen Gleichheitszeichen nicht.
Antwort: Jedes Gleichheitszeichen steht für eine Umformung. Schreiben Sie die Umformung, welche Sie nicht verstehen, extra auf ein Blatt Papier ab. Schauen Sie sie genau an, vielleicht kommt jetzt ein Gedanke. Wenn nicht, dann fragen Sie im Unterricht nach. Wenn Sie sagen, dass Sie alle Umformungen nicht verstehen: das glaube ich Ihnen nicht !
Frage: Ist Mathe in der ganzen Oberstufe so schwer?
Antwort: Nein ! Irgendwann glauben wir alle an Teil D und rechnen damit weiter, und dann wird alles viel einfacher.
- Empfohlene Übung: Wenn Sie Teil A verstanden haben: Berechnen Sie die Steigung von
 Das geht genauso, wenn am Schluss wieder „2“ rauskommt, haben Sie was falsch gemacht, wenn „3“ rauskommt, war es wahrscheinlich richtig. Übrigens,
Das geht genauso, wenn am Schluss wieder „2“ rauskommt, haben Sie was falsch gemacht, wenn „3“ rauskommt, war es wahrscheinlich richtig. Übrigens,  , wer das nicht glaubt bitte nachrechnen, der Beweis steht auch weiter unten im Teil C des Anhangs.
, wer das nicht glaubt bitte nachrechnen, der Beweis steht auch weiter unten im Teil C des Anhangs.
Also jetzt zum Beweis ! Wir benutzen die sogenannte „ -Methode“.
-Methode“.
Teil A
Die Funktion  hat an der Stelle
hat an der Stelle  eine Steigung von 2.
eine Steigung von 2.
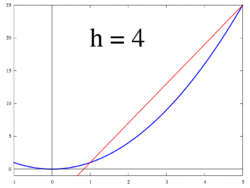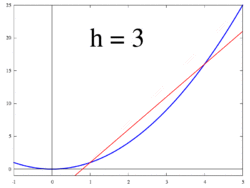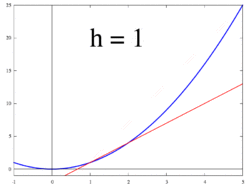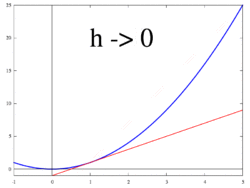
Vier Sekanten und eine Tangente: Zu den jeweiligen h-Werten sind die dazugehörigen Sekanten eingezeichnet. Für

geht die Sekante in die Tangente und somit die Sekantensteigung (Differenzenquotient) in die Tangentensteigung (Ableitung) über.
Die Steigung einer Funktion im Punkte  ist die Steigung ihrer Tangente, und die Tangentensteigung ist der Grenzwert von Sekantensteigungen.
ist die Steigung ihrer Tangente, und die Tangentensteigung ist der Grenzwert von Sekantensteigungen.
Wir betrachten deshalb zunächst für ein beliebiges, allgemeines  die Sekante durch die beiden Punkte
die Sekante durch die beiden Punkte  und
und  und berechnen ihre Sekantensteigung. Danach setzen wir Werte für
und berechnen ihre Sekantensteigung. Danach setzen wir Werte für  ein, die immer kleiner werden. Je kleiner das
ein, die immer kleiner werden. Je kleiner das  , um so besser die Annäherung der Sekantensteigung an die gesuchte Tangentensteigung. Wir betrachten jetzt sogar unendlich viele
, um so besser die Annäherung der Sekantensteigung an die gesuchte Tangentensteigung. Wir betrachten jetzt sogar unendlich viele  , die der Null beliebig nahe kommen, am einfachsten ist
, die der Null beliebig nahe kommen, am einfachsten ist  und so weiter. Damit kommen wir auch dem gesuchten Ergebnis beliebig nahe. Mathematisch bezeichnen wir das als „Grenzwert“, also läßt sich die gesuchte Tangentensteigung berechnen als Grenzwert von Sekantensteigungen mit „immer kleinerem“
und so weiter. Damit kommen wir auch dem gesuchten Ergebnis beliebig nahe. Mathematisch bezeichnen wir das als „Grenzwert“, also läßt sich die gesuchte Tangentensteigung berechnen als Grenzwert von Sekantensteigungen mit „immer kleinerem“  .
.
Die Steigung der Sekante ist
 ... (Binomische Formel)
... (Binomische Formel)- .......

Im Grenzwert gilt

Teil B
Die Funktion  hat an der Stelle
hat an der Stelle  eine Steigung von
eine Steigung von  .
.
Die Steigung der Sekante ist
 ... (Binomische Formel)
... (Binomische Formel)- .......

Im Grenzwert gilt

Teil C
Die Funktion  hat an der Stelle
hat an der Stelle  eine Steigung von n.
eine Steigung von n.
Die Steigung der Sekante ist
 ... (Binomische Formel)
... (Binomische Formel)- .......

Im Grenzwert gilt

Teil D
Die Funktion  hat an der Stelle
hat an der Stelle  eine Steigung von
eine Steigung von  .
.
Die Steigung der Sekante ist
 ... (Binomische Formel)
... (Binomische Formel)- .......

Im Grenzwert gilt

Anhang: Binomische Formeln
Jeder kennt 
Teil A: wir setzen  und
und  und erhalten
und erhalten

Teil B: wir setzen  und
und  und erhalten
und erhalten

Teil C: wir verallgemeinern die Formel aus Teil A,
zunächst für  , wir benutzen die für
, wir benutzen die für  (Binomische Formel)
(Binomische Formel)

Jetzt für  , wir benutzen die für
, wir benutzen die für 

Das könnten wir noch seitenlang weiter ausrechnen, in jeder Stufe kommt ein Summand hinzu und die Terme werden immer länger. Im Beweis brauchen wir aber eigentlich nur die ersten beiden Summanden, der Rest wird bei der Grenzwertbetrachtung sowieso zu Null. Darum schauen wir uns die Rechnungen mal genauer an:
- Der erste Summand „1“ im Ergebnis bleibt immer gleich , er stammt aus der linken Klammer, die rechte Klammer kann nichts dazu beitragen.
- Der zweite Summand (hier „4h“) stammt zum größten Teil (hier „3h“) aus der linken Klammer, aus der rechten Klammer wird er um genau ein h erhöht.
- Alles andere (hier „
 “) enthält Faktoren von
“) enthält Faktoren von  oder höher und laßt sich schreiben als
oder höher und laßt sich schreiben als  Rest.
Rest.
- Was genau der Rest ist, interessiert uns nicht, da sich ab
 im
im  sowieso alles wegkürzt.
sowieso alles wegkürzt.
Also können wir schreiben:





- (...) oder allgemein

Wir nehmen an, die Formel sei bereits gezeigt für den Exponenten n-1, für diesen lautet sie :
Allgemeiner Beweis für den Exponenten  , wir benutzen die bereits gezeigte Formel für
, wir benutzen die bereits gezeigte Formel für 

Diese Art von Beweis erinnert an das Umfallen einer Reihe von Dominosteinen: der vierte Stein stößt den fünften um, der fünfte den sechsten, allgemein der  te Stein den n-ten. In der Mathematik heißt dieses Prinzip „vollständige Induktion“.
te Stein den n-ten. In der Mathematik heißt dieses Prinzip „vollständige Induktion“.
Teil D: wir verallgemeinern die Formel aus Teil B, zunächst für  , wir benutzen die für
, wir benutzen die für 

Weiter geht es genauso wie in Teil C, und wir erhalten





- (...) oder allgemein

Allgemeiner Beweis für  , wir benutzen die bereits gezeigte Formel für
, wir benutzen die bereits gezeigte Formel für 






































































