Antireflexbeschichtung

aus Wikipedia, der freien Enzyklopädie
(Weitergeleitet von Entspiegelung)
In diesem Artikel oder Abschnitt fehlen noch folgende wichtige Informationen:
Der in der Einleitung erwähnte elementare Aspekt der Transmission bei einer Antireflexbeschichtung wird nicht behandelt; es fehlen plausible Diagramme zur Darstellung von destruktiver Interferenz, Transmission sowie der kausale Zusammenhang zwischen destruktiver Interferenz und Transmission; ferner die Erklärung des Verhaltens des Lichts unterhalb und oberhalb der destruktiven Interferenz (f0) als Aspekt der Notwendigkeit von Mehrschichtenvergütungen (Diskussion:Antireflexbeschichtung#Wie funktioniert eine Antireflexbeschichtung wirklich?).
Hilf der Wikipedia, indem du sie recherchierst und einfügst.

Antireflexbeschichtungen (kurz AR-Beschichtung) werden eingesetzt, um die Reflexion von optischen Oberflächen von Linsen, Objektiven, Prismen oder Platten zu unterdrücken und die Transmission zu erhöhen. Bei Objektiven und Okularen mit einer solchen Beschichtung spricht man hierbei von einer Vergütung, bei Brillen, Sichtfenstern oder Bildröhren von einer Entspiegelung. Als Erfinder der optischen Vergütung gilt der ukrainische Physiker Alexander Smakula.[1]

Grundlagen

Der einfallende Strahl wird an A und an B mit Phasensprung reflektiert. Die Strahlen r1 und r2 interferieren destruktiv zur Amplitude null.

Die Verminderung des Reflexionsgrades an der vergüteten Fläche wird durch eine destruktive Interferenz der reflektierten Strahlen erreicht.

Für den einfachsten Fall einer einzelnen, homogenen Vergütungsschicht betrachten wir einen Strahl einer bestimmten Wellenlänge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lambda_0} , der senkrecht einfällt (im Bild zur besseren Erkennbarkeit schräg gezeichnet). Er wird teilweise an der Oberfläche der Vergütungsschicht reflektiert (r1), und teilweise passiert er die Schicht und wird dann an der nächsten Grenzfläche teilweise reflektiert (r2). Damit die beiden Teilstrahlen r1 und r2 vollständig destruktiv interferieren, müssen ihre Amplituden gleich groß (Amplitudenbedingung) und gegenphasig (Phasenunterschied Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \pi} ) zueinander sein (Phasenbedingung).[2]

Aus den Fresnel’schen Formeln ergibt sich, dass der Brechungsindex Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n_1 } der Vergütungsschicht

betragen muss, damit die Amplituden von r1 und r2 gleich groß sind. Dabei ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n_2} der Brechungsindex des Stoffes und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n_0} der Brechungsindex des Mediums vor der Fläche (meistens Luft). Es wird hier vernachlässigt, dass der Strahl r2 an der Oberfläche der Vergütungsschicht nochmals reflektiert wird; genau genommen wird er unendlich oft hin und her reflektiert.

Datei:Reflexiongrad MgF2 auf SiO2.png
Reflexionsgrad für Licht der Wellenlänge λ0 = 580 nm in Abhängigkeit vom Einfallswinkel und der Dicke einer Magnesiumfluorid-Schicht (MgF2) auf einem Siliciumdioxidsubstrat.

Wegen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n_0 < n_1 < n_2 } findet bei der Reflexion sowohl bei Punkt A als auch bei B ein Phasensprung von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \pi} statt, genau genommen ein Vorzeichenwechsel der Amplitude, was auf die Interferenz keinen Einfluss hat. Für den nötigen Phasenunterschied von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \pi} muss also die optische Weglänge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta } des Strahls in der Vergütungsschicht

Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle \Delta =k{\frac {\lambda _{0}}{2}}\quad {\text{mit}}\quad k=1,3,5,\ldots }

betragen. Wenn man die dünnste mögliche Schicht verwendet (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k = 1 } ), ergibt sich mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta = 2 \; d \; n_1 } für die optimale Schichtdicke 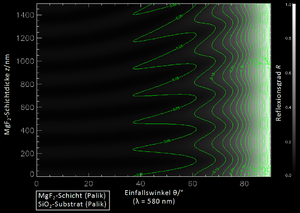Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d } :

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d=\frac{\lambda_0}{4 n_1}} .

Wenn der Strahl nicht senkrecht, sondern unter dem Winkel Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha } auf die Fläche trifft, verändert sich bei gleicher Schichtdicke die optische Weglänge in der Beschichtung nach dem Snellius’schen Brechungsgesetz und außerhalb durch den seitlich versetzten Austritt, so dass sich eine höhere optimale Schichtdicke ergibt bzw. bei gegebenen d eine Verkürzung der passenden Wellenlänge. Im Fall der destruktiven Interferenz und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k = 1} gilt (siehe auch [2][3]):

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \frac{\lambda_0}{d} = 4 \sqrt{n_1^2 - n_0^2 \sin^2 \alpha} }

Abweichende Wellenlängen werden zunehmend doch reflektiert bzw. interferieren nicht vollständig destruktiv. Das ist der Grund, warum die (schwache) Reflexion von vergüteten Oberflächen farbig ist und die Farbe winkelabhängig.

Beispiel einer Einfachvergütung

Als Beispiel betrachten wir den senkrechten Einfall von gelb-grünem Licht (550 nm Wellenlänge) auf Kronglas (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n_2 = 1{,}5} ). Das äußere Medium sei Luft (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n_0 \approx 1{,}0} ). Ohne Vergütung beträgt der Reflexionsgrad gemäß der Fresnel-Gleichungen

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R = \left( \frac{1{,}5-1}{1{,}5+1} \right)^2 = 0{,}2^2 = 4\,\%} .

Nach der Formel im vorangehenden Abschnitt wäre der ideale Wert für die AR-Schicht Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle n_{1}=1{,}22} , wofür jedoch kein haltbares Material zur Verfügung steht. Verwendet wird oft Magnesiumfluorid (MgF2, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n_1 = 1{,}38} ). Die λ/4-Schicht für das gelb-grüne Licht ist damit etwa 100 nm dick und ergibt bei senkrechtem Einfall einen Reflexionsgrad (Herleitung siehe u. a. Hecht[4] oder Pedrotti[5]) von

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle R = \left( \frac{1{,}5 \cdot 1-1{,}38^2}{1{,}5 \cdot 1 + 1{,}38^2} \right)^2 = 1{,}4\,\%} .

Mehrfachvergütung

Weiter und über einen breiteren Wellenlängen- und Winkelbereich kann die Reflexion verringert werden durch den Einsatz mehrerer übereinanderliegender Schichten mit unterschiedlichen Brechungsindizes. Für die optimalen Schichtdicken bei gegebener Wahl der Materialien gibt es keine einfache Formel. Diese Parameter werden daher mit Hilfe von Simulationsprogrammen bestimmt.

Herstellung

Die Herstellung von Antireflexionsbeschichtungen erfolgt durch Beschichtungsmethoden der Dünnschichttechnik. Zu den am häufigsten eingesetzten Verfahren gehören physikalische Gasphasenabscheidungen, wie thermisches Verdampfen und Sputterdeposition. Die Wahl der Beschichtungsmethode ist hauptsächlich von dem gewünschten Schichtmaterial abhängig, beispielsweise gibt es Materialien, die für das thermische Verdampfen nicht geeignet sind.

Die Antireflexionsschichten stellen hohe Anforderungen an die Gleichmäßigkeit der Schichtdicke. Denn ungleichmäßig vergütete Gläser zeigen Farbverläufe oder gar newtonsche Ringe und sind daher für viele Anwendungen unbrauchbar. Vergütete Flächen sind zudem empfindlich gegen Verschmutzung (Fingerabdrücke, Reste von Reinigungsmitteln), da diese ebenfalls eine dünne Schicht darstellen und somit die optischen Eigenschaften beeinflussen.

Anwendungsbereiche

Linsen und Objektive

Objektive mit zehn oder mehr Linsen, wie etwa Zoomobjektive, wären ohne Antireflexbeschichtung praktisch nicht einsetzbar: Licht kann nach zweimaliger Reflexion zusammen mit dem Nutzlicht aus dem Objektiv austreten und störende Lichtflecke (Reflexe) auf dem Bild verursachen oder als diffuser Schleier den Kontrast des Bildes vermindern. Bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k} Linsenoberflächen gibt es Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k (k-1) / 2 } Flächenpaare, an denen dies auftreten kann, d. h., der Effekt wächst quadratisch mit der Flächenzahl.

Die Verringerung des Reflexionsgrades an den Einzelflächen um einen Faktor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f} reduziert die Intensität der Reflexe um den Faktor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f^2} , da das Licht immer zweimal gespiegelt wird. Der positive Effekt durch die Vergütung wirkt sich also ebenfalls quadratisch aus.

Bei guten Fotoobjektiven sind alle Luft-Glas-Flächen mehrfachvergütet. In Fotoobjektiven werden vergütete Linsen seit den 1930er Jahren eingesetzt, die Mehrschichtvergütung hat sich aber erst in den 1970er Jahren bei hochwertigen Objektiven durchgesetzt und ist heute außer bei sehr einfachen Kameras und Objektiven Standard.

Manche optische Materialien für den infraroten Spektralbereich, etwa in Thermografie-Kameras, haben einen hohen Brechungsindex, z. B. einkristallines Germanium oder Zinkselenid, und weisen daher unbeschichtet hohe Reflexionsgrade auf.

Bei Objektiven für die Fotografie hat die Art der Vergütung bei modernen MC-Schichten nur einen sehr geringen Einfluss auf die Farbwiedergabe, weil der Anteil des noch reflektierten Lichts an der Gesamtenergie der hindurchtretenden Strahlung sehr gering ist und weil man verschiedene Vergütungen innerhalb eines Objektivs so kombiniert, dass die Gesamtreflexion an allen Flächen nur noch wenig von der Wellenlänge abhängt. Objektive können jedoch aufgrund ihrer spezifischen Gesamttransmission durchaus etwas „wärmer“ oder „kälter“ zeichnen, was jedoch in der Praxis meist nur in der Diafotografie von Bedeutung ist. Durch Änderung der Schichtdicken wird die Abhängigkeit von der Wellenlänge beeinflusst, dadurch entsteht der Farbeindruck der Objektivfrontlinsen.

Bei Brillen sind farbige Reflexe besonders unerwünscht. Deshalb wird dort breitbandig wirksame Mehrfachvergütung eingesetzt. Besonders wichtig sind entspiegelte Brillen für das Fahren im Dunkeln.

Hochleistungsoptiken

Die für die Beschichtung verwendeten Werkstoffe weisen meist höhere Absorption auf als die Werkstoffe der optischen Komponenten. Die Zerstörschwelle einer Antireflexbeschichtung durch thermische Belastung ist daher in der Regel geringer als diejenige einer unbeschichteten Grenzfläche. Man führt bei Hochleistungslichtleitkabeln den Strahl deshalb vor Eintritt oder nach Verlassen der Faser zunächst in einem Glasblock mit gleichem Brechungsindex weiter, bis er einen größeren Durchmesser hat. Dort kann dann eine Grenzfläche liegen, die auch antireflexbeschichtet werden kann.

Die Zerstörschwelle von beschichteten und unbeschichteten Laseroptiken wird bei kontinuierlicher Strahlung (CW) mit einer maximalen Leistungsdichte (z. B. Watt pro cm²) und bei gepulster Strahlung mit einer maximalen Energiedichte (z. B. Joule pro cm²) angegeben.

Kontinuierlich variierender Brechungsindex

Ein kontinuierlicher Übergang des Brechungsindex reduziert den Reflexionsgrad ohne starke Wellenlängen- und Winkelabhängigkeit. Für den Übergang auf n = 1 ist dafür allerdings ein Brechungsindex nahe bei 1 notwendig. Ein Forscherteam des Rensselaer Polytechnic Institute hat eine Beschichtung aus Siliziumstäbchen (vgl. Schwarzes Silizium) entwickelt, die einen Brechungsindex von lediglich 1,05 aufweist.[6][7] Die Entspiegelung durch Nanostrukturen an der Oberfläche wird auch Mottenaugen-Effekt genannt.

Volumenstrukturen

Das Konzept der Antireflexbeschichtung lässt sich auch von planaren Medien auf Systeme mit komplexer Volumenstruktur, wie z. B. ungeordnete Medien, verallgemeinern.[8] Die entsprechenden Antireflexstrukturen sind dann sorgfältig entworfene Anordnungen räumlich verteilter Elemente, deren Streueigenschaften auf das Medium abgestimmt sind, dessen Reflexion man unterdrücken möchte.

Einzelnachweise

  1. ↑ Josef Reiner: Grundlagen der Ophthalmologischen Optik. BoD – Books on Demand, 2002, ISBN 3-8311-2767-0, S. 72 (eingeschränkte Vorschau in der Google-Buchsuche).
  2. ↑ a b F. Pedrotti, L. Pedrotti, W. Bausch, Hartmut Schmidt: Optik für Ingenieure: Grundlagen. 3., bearb. u. aktualisierte Auflage. Springer, Berlin/Heidelberg 2005, ISBN 3-540-22813-6, S. 295–296.
  3. ↑ Eugene Hecht, Alfred Zajac: Optics. 4. Auflage. Addison-Wesley Longman, Amsterdam, 2003, ISBN 0-321-18878-0, S. 402.
  4. ↑ Eugene Hecht, Alfred Zajac: Optics. 4. Auflage. Addison-Wesley Longman, Amsterdam, 2003, ISBN 0-321-18878-0, S. 425.
  5. ↑ F. Pedrotti, L. Pedrotti, W. Bausch, Hartmut Schmidt: Optik für Ingenieure: Grundlagen. 3., bearb. u. aktualisierte Auflage. Springer, Berlin/Heidelberg 2005, ISBN 3-540-22813-6, S. 559–601.
  6. ↑ J.-Q. Xi, Martin F. Schubert, Jong Kyu Kim, E. Fred Schubert, Minfeng Chen, Shawn-Yu Lin, W. Liu, J. A. Smart: Optical thin-film materials with low refractive index for broadband elimination of Fresnel reflection. In: Nat Photon. Band 1, Nr. 3, Februar 2007, S. 176–179, doi:10.1038/nphoton.2007.26.
  7. ↑ Fred Schubert: New Nanocoating Is Virtual Black Hole for Reflections. Physorg.com, 1. März 2007.
  8. ↑ Michael Horodynski, Matthias Kühmayer, Clément Ferise, Stefan Rotter, Matthieu Davy: Anti-reflection structure for perfect transmission through complex media. In: Nature. Band 607, Nr. 7918, 14. Juli 2022, ISSN 0028-0836, S. 281–286, doi:10.1038/s41586-022-04843-6 (nature.com [abgerufen am 23. August 2022]).
Abgerufen von „https://de.wikiup.org/index.php?title=Antireflexbeschichtung&oldid=225572960“