Enzensberger-Stern
Der Enzensberger-Stern ist eine dreidimensionale algebraische Fläche, benannt nach dem Schriftsteller Hans Magnus Enzensberger. Die Deutsche Mathematiker-Vereinigung (DMV) hat am 10. November 2006 ihre Medienpreise im Leibnizsaal der Berlin-Brandenburgischen Akademie der Wissenschaften verliehen und dabei das Polynom 6. Grades
zu Ehren Enzensbergers mit gleichem Namen versehen.[1][2]
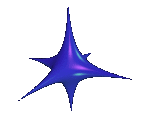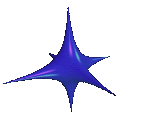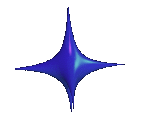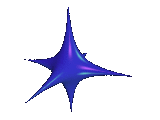
Die Fläche hat die Gestalt eines Sterns mit sechs Spitzen, die sich entlang der vierzähligen Symmetrieachsen eines Oktaeders ausbilden. Er besitzt dieselbe Symmetrie wie der Oktaeder bzw. der Hexaeder (Würfel). Die Spitzen sind durch elegant gekrümmte Flächen miteinander verbunden. Der Faktor 400 gibt dem Stern eine gefällige Form. Der Enzensberger-Stern hat vornehmlich den Charakter eines Kunstwerks und ist von geringerer mathematischer Bedeutung.
Weblinks
Einzelnachweise
- ↑ Rainer Schulze-Pillot: Medienpreis und Journalistenpreis der DMV. In: Mitteilungen der DMV. Band 15, Nr. 1, Februar 2007, ISSN 0947-4471, S. 22, doi:10.1515/dmvm-2007-0009.
- ↑ Jochen Brüning: Die Fläche des Poeten. In: Mitteilungen der DMV. Band 15, Nr. 1, Februar 2007, ISSN 0947-4471, S. 33–36, doi:10.1515/dmvm-2007-0014.