Eulerkraft

In der klassischen Mechanik ist die Eulerkraft (benannt nach Leonhard Euler) die auf einen Körper wirkende Scheinkraft, die in einem rotierenden Bezugssystem auftritt, wenn die Rotationsachse oder die Rotationsgeschwindigkeit sich zeitlich ändern.

Der Name wurde 1949 von Cornelius Lanczos in seinem Buch The Variational Principles of Mechanics eingeführt, wobei er gleichzeitig darauf hinwies, dass zu dieser Zeit kein allgemein gebräuchlicher Name für diese Trägheitskraft existierte.

Allgemeines

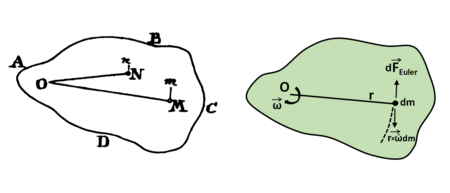
Die Eulerkraft ist gegeben durch:

${\begin{aligned}{\vec {F}}_{\mathrm {Euler} }&=-m\cdot {\frac {\mathrm {d} {\vec {\omega }}}{\mathrm {d} t}}\times {\vec {r}}\\&=-m\cdot {\vec {\alpha }}\times {\vec {r}}\end{aligned}}$

mit

• der Winkelgeschwindigkeit ${\vec {\omega }}$ des Bezugssystems,
• der Winkelbeschleunigung ${\vec {\alpha }}$ des Bezugssystems,
• dem Ortsvektor ${\vec {r}}$ des Punktes im Bezugssystem.

Siehe auch: Beschleunigtes Bezugssystem#Transformation der Beschleunigung

Die Eulerbeschleunigung ${\vec {a}}_{\mathrm {Euler} }$ (auch Azimutalbeschleunigung oder Transversalbeschleunigung; in der Physik ist die Bezeichnung „Eulerbeschleunigung“ kaum gebräuchlich) wird durch die Winkelbeschleunigung des Bezugssystems hervorgerufen:

${\vec {a}}_{\mathrm {Euler,TM} }={\vec {\alpha }}\times {\vec {r}}$

Die Eulerbeschleunigung gibt in der Technischen Mechanik (daher der Index TM) den von ${\vec {\alpha }}={\tfrac {\mathrm {d} {\vec {\omega }}}{\mathrm {d} t}}={\dot {\vec {\omega }}}$ abhängigen Teil der Führungsbeschleunigung an, die ein Punkt erfahren würde, der fest mit dem Bezugssystem verbunden ist. Er kommt durch die ungleichförmige Drehbewegung des Bezugssystems zustande.

Die oben definierte Eulerkraft ist der zugehörige Trägheitswiderstand:

$\Rightarrow {\vec {F}}_{\mathrm {Euler} }=-m\cdot {\vec {a}}_{\mathrm {Euler,TM} }$

Beispiele

Anfahrendes Karussell

Dies ist ein Beispiel für eine zeitliche Änderung der Rotationsgeschwindigkeit.

Eine Person, die in einem Kinderkarussell auf einem Pferd sitzt, spürt beim Anfahren die Eulerkraft. Es handelt sich um diejenige Trägheitskraft, die die Person beim Anfahren nach hinten vom Pferd zieht (und sie beim Anhalten nach vorne drückt). Die Richtung der Eulerkraft liegt hier in der Rotationsebene senkrecht zur Zentrifugalkraft. In diesem Beispiel mit fester Richtung der Drehachse ist die Eulerkraft nichts anderes als die Trägheitskraft $-m{\vec {a}}$, die ein Körper jeder Beschleunigung seiner Bewegung entgegensetzt ($m$ ist die Masse des Körpers und ${\vec {a}}$ die Beschleunigung ihrer Bahngeschwindigkeit).

Falls sich die Person beim ruckartigen Anfahren nicht fest hält, spürt sie in ihrem eigenen Bezugssystem keine Trägheitskraft, rutscht aber nach hinten vom Pferd herunter. Von außen betrachtet bleibt ihre Position unverändert, und das Pferd unter ihr fährt davon. Von einem Standpunkt in dem beschleunigt rotierenden Bezugsystem aus erscheint die Person aber nach hinten beschleunigt, was als Folge der in dem beschleunigt rotierenden Bezugsystem wirksamen Eulerkraft ${\vec {F}}_{\mathrm {Euler} }$ interpretiert wird.

Kippen der Drehachse

Neigt sich bei gleichbleibender Drehgeschwindigkeit eines Karussells die Drehachse zunehmend nach einer Seite, so erfährt die mitfahrende Person die Eulerkraft immer dann am stärksten, wenn ihr Ortsvektor senkrecht auf der Ebene steht, in der die Neigung sich vollzieht. Ihre Bahnkurve zeigt in diesen Punkten zusätzlich zur Krümmung aufgrund der Drehbewegung eine maximale Krümmung weg von der augenblicklichen Bahnebene.

Dagegen ist die Eulerkraft Null, wenn die Bahnkurve der Person durch die Ebene geht, in der sich die Drehachse neigt. Dann entspricht der zunehmenden Neigung der Achse nur eine gleichförmige Geschwindigkeit senkrecht zur Bahnebene.

Historische Bemerkung zur Eulerkraft

Die Eulerkraft kann bis zu Leonhard Eulers Werk zurückverfolgt werden, seine gesamte Mechanik der starren Körper basiert darauf.

In seinem dritten, späten Hauptwerk zur Mechanik, der Theoria Motus Corporum Solidorum et Rigidorum, erstmals 1765 erschienen, entwickelt Euler einen neuartigen, elementaren Ansatz zur Begründung sämtlicher Kraftwirkungen auf ausgedehnte Körper mit starren Verbindungen, der sich von der Newtonschen Kraftdynamik für Punktmassensysteme abgrenzt. Konzeptuell entspricht Eulers Ansatz der Anwendung des Prinzips nach d’Alembert, das von der Statik eines Körpersystems ausgeht und für dynamische Einwirkungen verallgemeinert wird. Er besagt in Kurzform:

Bei jeder infinitesimalen Rotation eines Körpers um eine feste Achse, die nicht durch den Massenmittelpunkt des Körpers verläuft, wird ein dynamisches Gleichgewicht der Drehmomente auf jedes Massenelement $\mathrm {d} m$ des Körpers erzeugt. Die verlorene, kompensierende Trägheitskraft tritt dabei in Form der Eulerkraft $\mathrm {d} {\vec {F}}_{\mathrm {Euler} }$ auf, deren Betrag $\mathrm {d} F_{\mathrm {Euler} }=\mathrm {d} m\cdot {\dot {\omega }}\cdot r$ ist.

Ausgehend von dieser „elementaren“ Kraft gelingt Euler die Verallgemeinerung für beliebige starre Körper, indem er über die jeweils wirkenden statischen Flächenmomente integriert. Daran schließt sich in den darauffolgenden Kapiteln der Theoria Motus ein erstmals systematischer Stand der Mechanik starrer Körper an. Zu der damaligen Zeit gehörten vor allem folgende Bereiche dazu: der Schwerpunktsatz, der allgemeine Momentensatz, eine allgemeine Theorie der Trägheitsmomente, die Theorie des Schwingungsmittelpunktes und die Kreiseltheorie.

Eulers Verfahren, die gesamte Mechanik der starren Körper aus der Elementarkraft $\mathrm {d} {\vec {F}}_{\mathrm {Euler} }$ zu entwickeln, konnte sich in den darauffolgenden Mechanikwerken nicht durchsetzen. Schon frühzeitig etablierte sich vielmehr die Lagrangesche Fassung des d’Alembertschen Prinzips, nach der die Eulerkraft nur als abgeleitete Größe, die aus Zwangs- oder Führungskräften gebildet wird, vorkommt.