Gergonne-Punkt

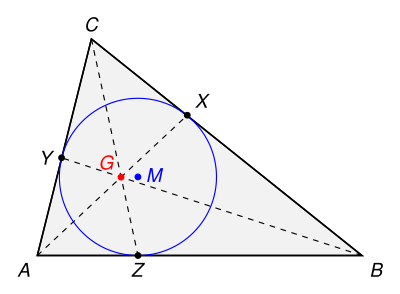
Der Gergonne-Punkt eines Dreiecks (benannt nach dem französischen Mathematiker Joseph Diaz Gergonne) ist ein ausgezeichneter Punkt im Inneren eines Dreiecks. Der Inkreis des Dreiecks $ABC$ hat den Mittelpunkt $M$ und berührt die Seiten des Dreiecks in den Punkten $X$, $Y$ und $Z$. Gergonne zeigte, dass sich die Verbindungsstrecken zwischen diesen Berührungspunkten und der jeweils gegenüberliegenden Ecke des Dreiecks in einem Punkt, dem Gergonne-Punkt $G$, schneiden.

Dass sich diese Strecken in einem Punkt schneiden, folgt aus ${\overline {AZ}}={\overline {AY}}$ usw. und dem Satz von Ceva.

Eigenschaften

• Der Gergonne-Punkt liegt mit dem Schwerpunkt und dem Mittenpunkt (in dieser Reihenfolge) auf einer Geraden.
• Gergonne-Punkt und Nagel-Punkt sind isotomisch konjugiert.

Koordinaten

Gergonne-Punkt ($X_{7}$)
Trilineare Koordinaten	${\frac {bc}{b+c-a}}\,:\,{\frac {ca}{c+a-b}}\,:\,{\frac {ab}{a+b-c}}$ $=\sec ^{2}{\frac {\alpha }{2}}\,:\,\sec ^{2}{\frac {\beta }{2}}\,:\,\sec ^{2}{\frac {\gamma }{2}}$
Baryzentrische Koordinaten	${\frac {1}{b+c-a}}\,:\,{\frac {1}{c+a-b}}\,:\,{\frac {1}{a+b-c}}$

Literatur

• Peter Baptist: Historische Anmerkungen zu Gergonne- und Nagel-Punkt. In: Sudhoffs Archiv, 71, 1987, 2, S. 230–233

Weblinks

• Eric W. Weisstein: Gergonne Point. In: MathWorld (englisch).
• Gergonne-Punkt – Visualisierung mit GeoGebra