Autobahndreieck

Ein Autobahndreieck ist ein dreiarmiger, höhenfreier Verkehrsknotenpunkt, an dem eine Autobahn in eine andere einmündet.
Straßenverkehrsrechtlich gesehen existiert der Begriff Autobahndreieck nur in Deutschland (Symbol ![]() , Kurzbezeichnung: AD). In der DDR und im Deutschen Reich wurde ein Dreieck als Abzweig bezeichnet. Sowohl in der Schweiz als auch in Österreich wird nicht zwischen Dreiecken und Kreuzen unterschieden: In der Schweiz werden diese als Autobahnverzweigung bezeichnet (Symbol:
, Kurzbezeichnung: AD). In der DDR und im Deutschen Reich wurde ein Dreieck als Abzweig bezeichnet. Sowohl in der Schweiz als auch in Österreich wird nicht zwischen Dreiecken und Kreuzen unterschieden: In der Schweiz werden diese als Autobahnverzweigung bezeichnet (Symbol: ![]() ), in Österreich als Knoten. Bei Einführung der Symbole für Knotenpunkte auf der Autobahnbeschilderung wurde auch in Deutschland nicht zwischen Kreuz und Dreieck unterschieden.
), in Österreich als Knoten. Bei Einführung der Symbole für Knotenpunkte auf der Autobahnbeschilderung wurde auch in Deutschland nicht zwischen Kreuz und Dreieck unterschieden.
Besteht zwischen zweien dieser Arme keine Verbindung, spricht man von einer Autobahngabelung. In Deutschland war dafür früher die Bezeichnung „Autobahnabzweig“ üblich, dort gilt dieser Begriff als treffender und ist dort noch der korrekte Fachbegriff.[1]
Autobahndreiecke befinden sich dort, wo eine Autobahn endet und in eine andere mündet oder wo ihr Verlauf unterbrochen ist. Im letzten Fall handelt es sich zwar um ein Dreieck, jedoch wird hier meist, zumindest teilweise, ein Autobahnkreuz gebaut und der Knotenpunkt auch bereits als Autobahnkreuz bezeichnet. Dadurch ist bei einem Weiterbau der Autobahn ohne großen baulichen Mehraufwand und ohne Umbenennung eine Inbetriebnahme möglich.
Bauteile
Die Bestandteile eines Autobahndreiecks entsprechen im Wesentlichen denen eines Autobahnkreuzes.
Bauformen
Es lassen sich drei Grundformen von Autobahndreiecken unterscheiden, sowie eine, die einem nicht fertiggestellten Autobahnkreuz entspricht. Alle Formen haben in Hinblick auf Wirtschaftlichkeit, Verkehrsaufkommen, Platzbedarf und Sicherheit Vor- und Nachteile.[2]

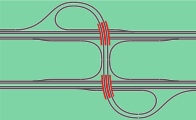
Dreieck
Bei dieser Bauform werden alle linksabbiegenden Fahrstreifen in einem großen Radius halbdirekt geführt. Dadurch sind hohe Geschwindigkeiten möglich. Es gibt dieses Dreieck in zwei Variationen je nach Schnittpunkt der Rampen: mit drei einzelnen Überwerfungen in zwei Etagen oder mit zwei Überwerfungen in drei Etagen, welches auch als halbes Malteserkreuz bezeichnet wird.
Der Einsatz dieser Bauform ist vor allem dort sinnvoll, wo in allen Richtungen eine hohe Verkehrsdichte herrscht. In Deutschland ist sie vorwiegend in Gegenden anzutreffen, die eine starke Verkehrsbelastung haben. In Österreich ist es die am häufigsten verwendete Form, in den USA sehr verbreitet und die bei Highways innerhalb von Ballungsräumen gängige Bauform.
- Beispiele für diese Bauform in Deutschland
- Hattenbacher Dreieck (50° 48′ 19″ N, 9° 31′ 50″ O) – Eine sehr große Form mit drei Brückenbauwerken an der A 7 / A 5. Anders als die Nummerierung der Autobahnen suggeriert, beschreibt die Relation Frankfurt am Main–Kassel (A 5–A 7) die durchgehende Fahrbahn.
- Viernheimer Dreieck (49° 33′ 21″ N, 8° 33′ 24″ O) – Sehr symmetrisch angelegtes Dreieck mit drei Brücken an der A 6 / A 67. Die durchgehende Fahrbahn bildet die Relation Frankfurt am Main–Karlsruhe (A 6–A 67).
- Autobahndreieck Karlsruhe an der A 5 / A 8.
- Autobahndreieck Würzburg-West (49° 44′ 42″ N, 9° 49′ 11″ O) – Bauform mit nur einem Brückenbauwerk an der A 3 / A 81. Das heutige Dreieck war als Malteserkreuz geplant.
- Autobahndreieck Frankfurt-Erlenbruch (50° 7′ 50″ N, 8° 43′ 30″ O) – Sehr symmetrische Bauform mit Trogbauwerken an der A 661 / A 66. Dieses Dreieck entsteht im Osten von Frankfurt am Main als Teil der Baumaßnahme Riederwaldtunnel.
- Beispiele für diese Bauform in Deutschland fast ohne Brücke
- Rosa-Luxemburg-Straße, Marie-Curie-Straße (50° 10′ 6″ N, 8° 37′ 46″ O). Die einzige Brücke hat die Rosa-Luxemburg-Straße, soll auch vierspurig in Nord-Süd-Richtung ausgebaut werden.
- Beispiel für diese Bauform in Österreich
- Knoten Innsbruck (47° 14′ 58″ N, 11° 23′ 54″ O) – An diesem Dreieck mit drei Brücken mündet die Brennerautobahn A13 in die Inntalautobahn A12. Die durchgehende Relation bilden die A13 und der östliche Teil der A12.
- Beispiele für diese Bauform in anderen Ländern
- Échangeur de Tournai (50° 37′ 48″ N, 3° 25′ 11″ O) – Sehr aufwändige Form eines Autobahndreiecks der A8 / A16 bei Tournai in Belgien. Innerhalb des Dreiecks befindet sich die voll ausgebaute Anschlussstelle Tournai, die aus insgesamt sieben Rampen besteht.
- Vor Qingdao in der Volksrepublik China ist ein Dreieck mitten in der Meeresbucht von Jiaozhou als Teil der Qingdao-Haiwan-Brücke eingebaut und liegt bei 36° 10′ 12″ N, 120° 17′ 54″ O.
- Autobahndreieck zwischen der Autoroute A6 und der Autoroute A31 bei Beaune in Frankreich.
- Autobahndreieck zwischen der Autoroute A40 und der Autoroute A42 bei Pont-d’Ain in Frankreich.
Dreieck ohne einheitliche Hauptrichtung
In den Richtlinien für die Anlage von Autobahnen (RAA) ist ein „Dreieck ohne einheitliche Definition der Hauptfahrbahnen“ definiert.[3] Dies ist ein höhenfreier dreiarmiger Verkehrsknoten, der aus drei Gabelungen besteht, deren jeweiliges Überwerfungsbauwerk nur die eine Fahrbahn der Gegenrichtung überführt, wodurch gegenüber der abzweigenden Straße in der Hauptrichtung ein TOTSO oder eine linksseitige Ausfahrt entsteht. Zwischen den Richtungsfahrbahnen entstehen Zwischenräume. Die Bauform ist in den USA mehrfach vorhanden. Ein Beispiel in Deutschland war bis 2007 auf der gelben Autobahn B7 (Brüsseler Straße) der Abzweig zur Düsseldorfer Straße im Westen des Stadtteils Oberkassel von Düsseldorf. 51° 14′ 3″ N, 6° 43′ 57″ O
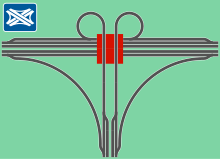
Trompete
Bei der sogenannten „Trompete“ wird ein linksabbiegender Fahrstreifen halbdirekt und einer indirekt geleitet. Diese Bauform ist kostengünstig, da nur ein Brückenbauwerk notwendig ist und verhältnismäßig wenig Fläche erforderlich ist. Allerdings ist die maximale Geschwindigkeit in der indirekt geführten Verbindungsrampe gering. Wegen der einfachen Bauform eignet sich die Trompete auch als Autobahnanschlussstelle, wenn der Zubringer an der Anschlussstelle endet. Der durch die Höhenfreiheit frei fließende Verkehr bringt keine Mehrkosten am Brückenbauwerk mit sich, da keine Verflechtung entsteht.
Es werden zwei Varianten der Trompete unterschieden: die rechts- und die linksgeführte.[4] Die Trompete ist in Deutschland häufig anzutreffen, die rechtsgeführte ist aber seltener, da der Verkehr ohne vorgeschalteten Verzögerungsstreifen in den engen Radius der Schleife geführt werden muss, was sich negativ auf die Verkehrssicherheit auswirkt. Daher wird diese Bauform bevorzugt nur dann realisiert, wenn der zur Verfügung stehende Platz keine andere Bauweise ermöglicht.
Beispiele der Trompeten-Bauform in Deutschland:
- Kirchheimer Dreieck (A 7 / A 4) – linksgeführt
- Autobahndreieck Fulda (A 7 / A 66) – linksgeführt
- Autobahndreieck Düsseldorf-Süd (A 46 / A 59) – rechtsgeführt
- Autobahndreieck Nordharz (A 36 / A 369) – linksgeführt
- Autobahndreieck Halle-Süd (A 38 / A 143) – linksgeführt
- Autobahndreieck Inntal (A 8 / A 93) – linksgeführt
- Autobahndreieck Saarlouis (A 8 / A 620) – rechtsgeführt
- Autobahndreieck Oldenburg-West (A 28/A 293) – rechtsgeführt
- Autobahndreieck Südharz (A 38/A 71) – rechtsgeführt
- Autobahndreieck Werntal (A 71 / A 70) – rechtsgeführt
- Autobahndreieck Friedrichsthal (A 8 / A 623) – rechtsgeführt
- Autobahndreieck Drammetal (A 7 / A 38) – rechtsgeführt
- Autobahndreieck Treptow (A 117 / B 96a) – rechtsgeführt
Eine Trompete im Wasser ist nördlich auf Taipa (Macau) auf der Estrada Alm. Magalhaes Correia zur Pte. da Amizade, der Brücke zum Flughafen zu finden. 22° 9′ 56″ N, 113° 33′ 50″ O
22° 16′ 52″ N, 114° 10′ 49″ O
Eingeschmolzene Trompete
Bei der eingeschmolzenen Trompete ist im Unterschied zur Trompete die durchgehende Fahrtrichtung gegenüber dem mündenden Verkehrsweg räumlich getrennt, um den mündenden Verkehr durch Verflechtung zu verbinden. Hierdurch entstehen (bei Rechtsverkehr) linksseitige Anschlüsse. Nach einer Wendeschleife wird die Gegenrichtung wiederum durch Verflechtung angebunden. Die Verflechtungen liegen außerhalb des Brückenbauwerkes und sind die einzige Kapazitätsbegrenzung bei einspuriger Ausführung. Diese Bauform benötigt die geringste Brückenfläche, jedoch mehr Raum. Nur eine Richtungsfahrbahn muss von einer weiteren überbrückt werden. Technisch ist das ein von innen gespeister, entflochtener, tropfenförmiger Turbokreisverkehr, der die Hauptrichtungen nicht unterbricht, oder eine Autobahngabelung ohne Hauptrichtung mit nachfolgender linksseitiger Wendeschleife, wodurch weitere teure Fläche innerhalb der Überwerfung eingespart wird. Die Wendeschleife ähnelt dem Michigan Left. Ein anderer Ansatz zur Beschreibung ist der Ausbau einer Gabelung zum Dreieck durch räumliche Trennung der Richtungsfahrbahnen. Im Westen des US-Bundesstaates Texas endet die Interstate 20 an der Interstate 10 bei 31° 5′ 25″ N, 104° 3′ 9″ W in dieser Bauform. In Florida finden sich mehrere Verkehrsknoten dieser Art.

Doppeltrompete
Zwei Trompeten kommen zum Einsatz, wenn zwei Autobahnen oder autobahnähnliche Straßen sich stark annähern, sich jedoch nicht oder erst an anderer Stelle kreuzen, oder wenn nachträglich eine Verbindung geschaffen wird. In diesem Fall wird ein kurzes autobahnartiges Verbindungsstück eingefügt, wodurch zwei dreiarmige Knotenpunkte (Trompeten) entstehen. In diesem Fall sind die Mundstücke der Trompeten direkt miteinander verbunden. Gegenüber einem Kreuz bilden die beiden T-Stücke H-förmig eine 4-armige Verbindung. Dies wird in Italien, Japan und USA bevorzugt eingesetzt, um Mautstraßen mit mautfreien Straßen zu verbinden. Dabei werden die Fahrzeuge nach Fahrziel gemischt, aber nach Auffahren und Verlassen der Mautstraße sortiert. Beispiele für Doppeltrompeten sind:
- Das Gießener Nordkreuz besteht aus zwei linksgeführten Trompeten.
- Die Verbindung zwischen der A 45 bei Dillenburg und der B 277 bei 50° 44′ 38″ N, 8° 15′ 37″ O.
- Die Anschlussstelle Trier-Ehrang, die bei 49° 48′ 7″ N, 6° 42′ 31″ O die A 602 mit der B 52 verbindet.
Eine Sonderform der Doppeltrompete mit fehlenden direkten Rampen ist die Büroklammer. Verwandt ist die indirekte Trompete.
Zudem existieren Doppeltrompeten, deren Trichter auf dieselbe Autobahn münden.[5] Dies könnte die Bauform für ein Autobahnkreuz sein, wenn die Ausfahrrampe einer abzweigenden Autobahn links angebracht werden darf oder zwei Autobahnen an der durchgehenden enden. Da die Ohren mit je zwei Fahrtrichtungen ineinander liegen, wird erheblich Platz gespart.
- In der norwegischen Stadt Bergen verbindet eine der kompaktesten Doppeltrompeten die E39 und die endende E18, die Fjøsangerveien und Sotraveien (Autobahn 555) bei 60° 23′ 1,1″ N, 5° 20′ 9,4″ O.
- Eine Doppeltrompete ist die Järnbrott-Kreuzung (Järnbrottsmotet), die im Süden von Göteborg bei 57° 38′ 45,5″ N, 11° 55′ 51,4″ O die Landstraße 158 mit der Dag-Hammarskjöld-Autobahn auf dem Gelände und den beiden Brücken des bis in die 1990er Jahre existierenden Europa-Kreisels verbindet. Dies wird durch zwei Zwischenrampen ermöglicht.
- In South Carolina bei Myrtle Beach kreuzen sich 10 km vor der Atlantikküste die US-501 und der Carolina Parkway, der SR-31 bei 33° 44′ 26″ N, 78° 57′ 6,4″ W.
- In Vermont nördlich von Bennington, bei 42° 54′ 15,3″ N, 73° 12′ 15″ W entsteht eine verschmolzene Doppeltrompete mit zwei durch die Bauform verkürzten Rampen; ein leistungsstarker Knoten, der die US-7 mit der VT-SR-279 verbindet.
- In Singapur ist der platzsparende Knoten zweifach vertreten: zwischen den Expressways Bukit Timah und Seletar bei 1° 25′ 17,1″ N, 103° 46′ 16,9″ O und bei 1° 19′ 31,5″ N, 103° 58′ 20,4″ O am East Coast Parkway zur Changi Coast Road und der Xilin Avenue.
- Eine prinzipverwandte Konstruktion ist das Autobahndreieck Moseltal, das aus zwei rechtsgeführten Trompeten besteht und lagebedingt noch zwei indirekte Rampen benötigt, um die L145 über die L150 in alle Richtungen einzubinden.
- Eine Doppeltrompete war rund 50 Jahre lang die Anschlussstelle Telegraph Road (ein Teil der US-24) zur Interstate 94 in Taylor, südlich gelegen im Großraum von Detroit im US-Bundesstaat Michigan bei 42° 15′ 52,9″ N, 83° 16′ 13,5″ W. Die 2005 zur SPUI zurückgebaute Anschlussstelle verlor um den Preis der Verlagerung der Ausfahrten auf die rechte Seite der Interstate ihren freien Verkehrsfluss. Im Zuge dessen wurden die Richtungsfahrbahnen der Interstate näher aneinander gelegt.[6]
„Trompete“, vor dem Ausbau zum vollen Kleeblatt, angewendet an den Autobahnkreuzen Ratingen-Ost, Dortmund-Nordwest und am Seligenstädter Dreieck
Birne
Bei einem Autobahndreieck in Birnenform, dem Pendant zur Turbine, werden beide linksabbiegende Fahrstreifen halbdirekt geführt. Dies ermöglicht ein Durchfahren mit hoher Geschwindigkeit, benötigt allerdings auch mehr Platz als die Trompete, und es sind zwei Brückenbauwerke notwendig.
Diese Bauform ist in Deutschland recht selten anzutreffen, da sie sowohl im Hinblick auf die Kosten als auch den Platzbedarf keine gravierenden Vorteile gegenüber den anderen Varianten hat. Als Birne war z. B. das Autobahndreieck Braunschweig-Südwest (A 39 / A 391) bis 2011 gebaut. Auch die neue Form des Dreiecks ist an die Birne angelehnt. Das im Juni 2015 eröffnete Autobahndreieck Bochum-West ist ebenfalls an die Bauform der Birne angelehnt, hier befindet sich eine der halbdirekten Rampen allerdings außerhalb der direkten Rampen.
Halbes Kleeblatt
Das halbe Kleeblatt (auch Teilkleeblatt, in der Schweiz Öse[7]) stellt einen Sonderfall unter den Autobahndreiecken dar. Es kommt ausschließlich dann vor, wenn bereits beim Bau ein Ausbau zum Autobahnkreuz als Kleeblatt geplant wird. Der gesamte Ausbauzustand ist dabei im Normalfall so ausgelegt, dass eine Erweiterung zum vollständigen Autobahnkreuz ohne Umbauten der bestehenden Bauwerke möglich ist. Meist sind nur diejenigen direkten und indirekten Verbindungsrampen fertiggestellt, die auch genutzt werden. Das zentrale Brückenbauwerk ist aber in voller Breite ausgebaut. Gegenüber der Trompete hat das halbe Kleeblatt eine Verflechtungsstrecke.
Beispiele für diese Bauform gibt es in Deutschland viele. Sie sind ein eindeutiges Indiz für die geplante – und teils auch wieder verworfene – Weiterführung von Autobahnen. Im Gegensatz zu anderen Varianten von Autobahndreiecken tragen sie meist auch bereits die Bezeichnung Autobahnkreuz:
- Autobahndreieck Holledau (A 9 / A 93)
- Autobahnkreuz Dortmund/Witten (A 44 / A 45)
- Dreieck Löhne (A 30 / B 61)
Mathematische Zusammenhänge
Es lässt sich mathematisch ermitteln, wie viele theoretisch mögliche Autobahndreiecke es gibt.
Um dies berechnen zu können, kann man sich vorstellen, dass 3 Autobahnen auf ein Autobahndreieck zulaufen, auch wenn in der Realität oft zwei dieser Autobahnen direkt miteinander verbunden sind. Diese Autobahnen werden im Folgenden mit A, B, C bezeichnet.
Die auf ein Autobahndreieck zulaufenden Fahrstreifen jeder Autobahn verzweigen sich in 2 Richtungen zu den jeweils anderen 2 Autobahnen. Dabei liegt die eine Abzweigung links von der anderen. In der Realität stellt die linke Abzweigung sozusagen die "Geradeausspur" dar. Die linke Abzweigung kann entweder an die eine oder andere Autobahn angebunden werden. Für die rechte Abzweigung ist dann eindeutig klar, an welche Autobahn sie angebunden wird. Dafür gibt es also 2 Möglichkeiten.
Genau die gleichen Betrachtungen gelten unabhängig für die vom Autobahndreieck wegführenden Fahrstreifen. Auch hier gibt es 2 Richtungen, sodass jeweils 2 Zusammenführungen mit den anderen 2 Autobahnen entstehen. Also gibt es für eine Autobahn insgesamt 2 · 2 = 4 Möglichkeiten. Die Betrachtungen für die anderen beiden Autobahnen sind natürlich gleich und ebenfalls davon unabhängig.
Daraus folgt, dass es für ein gesamtes Autobahndreieck genau 4 · 4 · 4 = 64 Möglichkeiten für die Anbindung aller Abzweigungen gibt.
Hinweis: In der Realität werden Abzweigungen meist mit Wegweisern ausgeschildert. Die Abzweigungen können Abfahrten oder Auffahrten sein. In der Realität können sie aber auch Weiterführungen derselben Autobahn sein, zum Beispiel beim Autobahndreieck „Birne“ und „halbes Kleeblatt“.
Im Folgenden betrachten wir die Autobahn A. Die linke Abzweigung wird mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \uparrow} A1, die rechte Abzweigung mit A2, die linke Zusammenführung mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \downarrow} A1 und die rechte Zusammenführung mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \downarrow} A2 bezeichnet.
Die Abzweigungs- und Zusammenführungsmöglichkeiten können wie folgt notiert werden:
| Abstrakte Darstellung für die Autobahn A eines Autobahndreiecks | ||||||
|---|---|---|---|---|---|---|
| Abzweigungen | Zusammenführungen | zugeordnete Farben | ||||
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \uparrow A_1 \rightarrow B} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \uparrow A_2 \rightarrow C} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \times} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \downarrow A_1 \leftarrow B} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \downarrow A_2 \leftarrow C} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \leftrightarrow} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_1: \quad \mathrm{rot}} |
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_2: \quad \mathrm{gelb}} | ||||||
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \uparrow A_1 \rightarrow C} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \uparrow A_2 \rightarrow B} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \downarrow A_1 \leftarrow C} | Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \downarrow A_2 \leftarrow B} | |||
| Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle f_4: \quad \mathrm{blau}} | ||||||
Hinweis: Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \times} steht für kartesisches Produkt, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \leftrightarrow} steht für bijektive Funktion.
Dabei wird das sozusagen das kartesische Produkt der 2 Möglichkeiten für die Abzweigungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \uparrow} A1 und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \uparrow} A2 der und der 2 Möglichkeiten für die Zusammenführungen A1 und A2 gebildet. Diese 2 Möglichkeiten sind die 2 Permutationen der Autobahnen B und C, und zwar jeweils für die Abzweigungen und die Zusammenführungen. Daraus ergeben sich 2 · 2 = 22 = 4 Kombinationen für jede der 3 Autobahnen A, B, C.
Diese 4 Kombinationen können zum Beispiel den 4 Farben f1 (rot), f2 (gelb), f3 (grün), f4 (blau) bijektiv zugeordnet werden. Die 3 Autobahnen können zum Beispiel 3 Perlen zugeordnet werden.
Als bijektive Analogie ergibt sich daraus eine Perlenkette mit 3 Perlen, die jeweils unabhängig eine von 4 Farben haben können. Für die Anzahl der möglichen Perlenketten erhält man also insgesamt (2 · 2)3 = (22)3 = 22 · 3 = 26 = 64 mögliche Kombinationen. Dabei werden gedrehte und gespiegelte Varianten der Perlenkette mitgezählt, wenn sie verschieden sind. Also gibt es auch 64 mögliche Kombinationen für ein ganzes Autobahndreieck. Dabei wird davon ausgegangen, dass die Autobahnen A, B, C festgelegt sind, also nicht durch Drehung oder Spiegelung vertauscht werden können.
Wenn die Autobahnen A, B, C nicht festgelegt sind, reduziert sich die Anzahl der möglichen Kombinationen auf 24. Bei diesen Kombinationen ist nicht die genaue geographische oder geometrische Anordnung der Fahrstreifen entscheidend, wie sie zum Beispiel auf einem Satellitenfoto sichtbar ist, sondern nur die zweidimensionale räumliche Zuordnung und Anordnung der Abzweigungen und Anbindungen, also die graphentheoretische Isomorphie. Die von oben sichtbaren Überschneidungspunkte der Abzweigungen, die üblicherweise durch Autobahnbrücken realisiert werden, werden bei der Betrachtung dieser Kombinationen nicht berücksichtigt.
Verallgemeinerung für ein Autobahnkreuz
Ein Autobahnkreuz hat 4 Autobahnen, die mit A, B, C, D benannt werden können. Wenn die Autobahnen A, B, C, D festgelegt sind, ergeben sich für ein Autobahnkreuz entsprechend (3! · 3!)4 = ((3!)2)4 = (62)4 = 62 · 4 = 68 = 1679616 mögliche Kombinationen. Dabei ist zu beachten, dass es für jede der 4 Autobahnen jeweils genau 3! = 6 Permutationen (Möglichkeiten) zu den 3 anderen Autobahnen gibt, und zwar jeweils für die Abzweigungen und die Zusammenführungen.
Wenn die Autobahnen A, B, C, D nicht festgelegt sind, reduziert sich die Anzahl der möglichen Kombinationen auf 420246 Möglichkeiten. Das kann mit einem Computerprogramm gezeigt werden.
Für die Verallgemeinerung mit n Autobahnen, einen hypothetischen "Autobahn-Stern", ergeben sich mithilfe der Permutationen der jeweils n − 1 anderen Autobahnen genau ((n − 1)! · (n − 1)!)n = (((n − 1)!)2)n = ((n − 1)!)2 · n mögliche Kombinationen.
Siehe auch
Weblinks
- Ágnes Lindenbach: Planfreie Knotenpunkte. (PDF; 410 kB) Vorlesung 2, Straßen und Eisenbahnwesen II. BMEEOUV-N40. Technische und Wirtschaftswissenschaftliche Universität Budapest, S. 2–5, archiviert vom Original am 5. Juli 2015; abgerufen am 15. März 2017.
- Adolf Elsaesser: Städte an den Hafrabastrassen. (PDF; 1,5 MB) III. Mannheim. In: Hafraba-Mitteilungsblatt. 1930, abgerufen am 15. März 2017 (Artikel von 1930 zur kreuzungsfreien Einlenkung Mannheim und Heidelberg).
- Autobahnkreuze & Autobahndreiecke in Deutschland (Datenbank mit Karten- und Luftbilddaten). (Memento vom 30. März 2016 im Internet Archive) (im archive.org)
Einzelnachweise
- ↑ Autobahnabzweig: RAS 1968 (BRD) RIST 1990 (DDR) Neufert (1937, 1980, 1996).
- ↑ Richtlinien für die Anlage von Straßen. Teil: Walter Durth (Hrsg.): Linienführung. RAS-L. Forschungsgesellschaft für Straßen- und Verkehrswesen, Köln 1995, ISBN 3-7812-1400-1.
- ↑ Institut für Straßen- und Eisenbahnwesen am KIT: Entwurf und Bau von Straßen – Teil: Straßenentwurf. (PDF; 8,44 MB). Abgerufen am 7. September 2013.
- ↑ Günter Wolf: Straßenplanung. Werner Verlag, München 2005, ISBN 3-8041-5003-9, S. 269.
- ↑ Joseph E. Hummer: Introduction to and Update on Unconventional Interchanges. (Memento vom 16. Dezember 2014 im Internet Archive) Regional Transportation Alliance, Raleigh, NC, abgerufen am 27. Juni 2014, S. 43.
- ↑ Historisches Luftbild im Museum of Ridiculous Highway Design. Abgerufen am 28. März 2013.
- ↑ Schweizer Norm 640 250 Knoten; Grundlagenorm, Ausgabe 1998, S. 7
Anmerkungen
- Google Earth hat Luftbilder zu diesem Thema. In der Mobilversion und dem Earth-Plug-in von Google Maps sind keine historischen Luftbilder verfügbar.