Korpuskeltheorie

aus Wikipedia, der freien Enzyklopädie

Die Korpuskeltheorie (auch Emissionstheorie oder ballistische Lichttheorie) ist eine vor allem Isaac Newton zugeschriebene physikalische Theorie, nach welcher das Licht aus kleinsten Teilchen oder Korpuskeln (Körperchen) besteht. Die Korpuskeltheorie wurde im 19. Jahrhundert durch die Wellentheorie des Lichtes abgelöst, jedoch werden dem Licht seit der Photonentheorie von Albert Einstein (1905) teilweise wieder auch korpuskulare Eigenschaften zugeschrieben.

Da die ursprüngliche Emissionstheorie mit dem Relativitätsprinzip und somit mit dem Michelson-Morley-Experiment verträglich ist, wurden zu Beginn des 20. Jahrhunderts solche Modelle erneut diskutiert und als Alternative zur Relativitätstheorie in Betracht gezogen. Jedoch wäre in der Emissionstheorie die Lichtgeschwindigkeit von der Geschwindigkeit der Lichtquelle abhängig, was durch eine Reihe anderer Experimente eindeutig widerlegt wurde. Ebenso wurde niemals eine vollständig durchgearbeitete Theorie vorgelegt. Folglich kann die Emissionstheorie nicht mehr in Betracht gezogen werden.[1][2][3]

Bis zum 19. Jahrhundert

Es gibt in der Wissenschaftsgeschichte viele verschiedene Emissionstheorien. Bereits Pythagoras und Empedokles hatten Emissionstheorien der Sinneswahrnehmung entwickelt. Auch Augustinus bezeichnete den Sehvorgang als „Strahlenwurf aus unseren Augen“.[4] Zahlreiche Emissionstheorien sind entstanden und wieder in Vergessenheit geraten. Emissionstheoretiker waren zum Beispiel Sir Isaac Newton (1643–1727), Pierre Simon de Laplace (1749–1827), Jean-Baptiste Biot (1774–1862), Sir David Brewster (1781–1868).

Die Korpuskeltheorie des Lichts besagt, dass das Licht aus winzigen Teilchen bzw. Korpuskeln besteht, die von den leuchtenden Körpern mit großer Geschwindigkeit geradlinig ausgeschleudert bzw. emittiert werden, wobei die Lichtgeschwindigkeit abhängig von der Geschwindigkeit der Lichtquelle ist. Diese Theorie konnte sowohl die geradlinige Ausbreitung, wie auch die Reflexion des Lichtes erklären. Ebenfalls können verschiedene Farben durch Annahme verschiedener Größe der Lichtteilchen erklärt werden. Beugung, Brechung an Grenzflächen oder teilweise Reflexion bereiten allerdings Schwierigkeiten. Die Brechung wurde so erklärt: In größerem Abstand zu Grenzflächen sind die Lichtteilchen allseitig von (anderen) gleichartigen Teilchen umgeben und fliegen deshalb geradlinig. An der Grenzfläche zweier verschieden „dichter“, transparenter Stoffe werden die „Lichtteilchen“ unterschiedlich stark angezogen und ändern deshalb schlagartig die Flugrichtung. Damit verbunden war die Vermutung, dass das Licht im „optisch dichteren“ Medium schneller fliegt.[5] Erst viel später, nach 1820, wurde gezeigt, dass die Lichtgeschwindigkeit im „optisch dichteren“ Medium kleiner ist als beispielsweise im Vakuum (snelliussches Brechungsgesetz). Obwohl also die Begründung für „optisch dichter“ falsch ist, wird dieser Ausdruck heute noch verwendet.

Einige Forscher zogen aus der korpuskularen Natur des Lichts weitergehende Schlüsse: Newton deutete bereits 1704 eine mögliche Ablenkung von Lichtstrahlen durch die Schwerkraft an, ohne jedoch die Ablenkung zu berechnen.[6][7] John Michell (1783)[8] und unabhängig von ihm Pierre-Simon Laplace (1796)[9] folgerten, dass derart massereiche Sterne vorstellbar seien, dass selbst das Licht ihnen nicht entkommen könnte, d. h., sie entwarfen eine Frühform eines Schwarzen Lochs. Schließlich (1801, veröffentlicht 1804) berechnete Johann Georg von Soldner die von Newton angedeutete Lichtablenkung, wobei er für unsere Sonne den Wert von 0,84″ erhielt,[10] was allerdings nur im Rahmen der Newtonschen Gravitationstheorie korrekt ist. Zur Ermittlung des korrekten Werts muss die aus der allgemeinen Relativitätstheorie folgende Raumkrümmung berücksichtigt werden, wodurch sich der Newtonsche Wert verdoppelt, wie Albert Einstein errechnete. Diese Voraussage wurde experimentell vielfach bestätigt.

In der Frage, ob denn die von Christiaan Huygens (1690) begründete, auf den Äther basierende Wellentheorie des Lichtes oder die Korpuskeltheorie richtig sei, siegte vorerst Newton. Im 19. Jhd. wurde Newtons Modell allerdings vor allem durch die Arbeiten von Thomas Young (1800), Augustin Jean Fresnel (1816) und James Clerk Maxwell (1864) überwunden und die Wellentheorie schien bewiesen zu sein. Dies folgte einerseits aus der Tatsache, dass Effekte wie Brechung und Beugung (insbesondere in Form des Poisson-Flecks) mittels der Wellentheorie sehr viel einfacher erklärt werden konnten, während im Rahmen der Korpuskeltheorie immer wieder Hilfshypothesen eingeführt werden mussten. Ebenso die Übereinstimmung in der Lichtgeschwindigkeit verschiedener Lichtstrahlen sprach für das Wellenmodell. Entscheidend war jedoch die bereits oben erwähnte Voraussage der Korpuskeltheorie, wonach Licht in dichteren Medien schneller sein müsste als in weniger dichten. 1850 konnte Léon Foucault erstmals mittels der Drehspiegelmethode die Lichtgeschwindigkeit in Medien ermitteln und fand heraus, dass sie in Luft größer war als in Wasser, was den Voraussagen der Wellentheorie entsprach. Dies wurde als endgültige Widerlegung der Korpuskeltheorie aufgefasst.[11][12][5]

Seit der Photonentheorie von Einstein (1905) werden dem Licht teilweise wieder auch korpuskulare Eigenschaften zugeschrieben, jedoch besitzen Photonen gemäß der Relativitätstheorie keine Masse, sondern lediglich Energie und Impuls. Im Rahmen der Quantenmechanik wird auch vom Welle-Teilchen-Dualismus gesprochen.

20. Jahrhundert

Emissionstheorien beruhen gewöhnlich auf der Annahme, dass sich das Licht ausschließlich in Bezug zur Lichtquelle konstant mit Lichtgeschwindigkeit ausbreitet – im Gegensatz zur (stationären) Äthertheorie, wonach sich Licht konstant in Bezug zum Äther ausbreitet, und im Gegensatz zur speziellen Relativitätstheorie (SRT), wonach sich Licht konstant in allen Inertialsystemen ausbreitet. Daraus folgt, wie in der ursprünglichen newtonschen Korpuskeltheorie, dass die Lichtgeschwindigkeit abhängig von der Geschwindigkeit der Lichtquelle ist. Der Wechsel des Inertialsystems erfolgt durch die Galilei-Transformation, wodurch das klassische Relativitätsprinzip erfüllt wird.[13] Das heißt, im Gegensatz zur Äthertheorie ist bei der Emissionstheorie ausschließlich die Relativbewegung von Quelle und Empfänger für den Dopplereffekt , als auch für die Aberration verantwortlich. Ähnliche Überlegungen wurden gelegentlich auch auf elektromagnetische Wellen übertragen, nicht nur auf Teilchen, wobei aber unterschiedliche Vorstellungen über die Quellenabhängigkeit der Lichtgeschwindigkeit einflossen.[14]

Da eine Emissionstheorie im Gegensatz zur Äthertheorie das klassische Relativitätsprinzip nicht verletzt und somit mit den erfolglosen Ätherdriftexperimenten (wie dem Michelson-Morley-Experiment) verträglich ist, wurde sie zu Beginn des 20. Jahrhunderts als Alternative zur lorentzschen Elektrodynamik und der SRT wieder in Betracht gezogen. Dies geschah vor allem deswegen, um die mit der Konstanz der Lichtgeschwindigkeit in allen Inertialsystemen einhergehende radikale Änderung des Verständnisses von Raum und Zeit zu vermeiden. Albert Einstein selbst zog vor 1905 eine Emissionstheorie in Erwägung, jedoch verwarf er sie noch vor 1905, da er sie als unverträglich mit den gewonnenen Erkenntnissen der Elektrodynamik ansah.[15][3][2]

Während das Licht sich in den meisten Emissionsmodellen konstant in Bezug zur ursprünglichen Lichtquelle ausbreitet, gab es unterschiedliche Vorstellungen, was überhaupt als Lichtquelle zu bewerten ist und ob auch Spiegel dazu gezählt werden dürfen. Daraus entwickelten sich verschiedene kinematische Varianten von Emissionstheorien[13][1]:

  • Licht breitet sich ausschließlich konstant in Bezug zur ursprünglichen Lichtquelle aus, unabhängig davon, ob es später an einem Spiegel reflektiert wird. Das heißt, das Zentrum der sphärischen Welle bewegt sich immer mit derselben Geschwindigkeit wie die ursprüngliche Lichtquelle. Dieses Modell wurde durch Walter Ritz 1908 vorgeschlagen und galt als die am weitesten entwickelte Emissionstheorie.[16]
  • Jeder Körper ist als neue Lichtquelle zu betrachten. Das heißt, ein Spiegel, der von einem Lichtstrahl getroffen wird und diesen reflektiert, fungiert als neue Lichtquelle, relativ zu dem sich das Licht nun konstant mit Lichtgeschwindigkeit ausbreitet. Licht breitet sich also als eine sphärische Welle aus, dessen Zentrum sich mit der Geschwindigkeit des jeweils letzten Körpers bewegt, von dem das Licht zuletzt reflektiert wurde. Dieses Modell wurde von Richard C. Tolman 1910 vorgeschlagen (wobei Tolman selbst Einsteins Relativitätstheorie bevorzugte).[17]
  • Licht, welches von einem Spiegel reflektiert wird, breitet sich von nun an mit der Geschwindigkeit des Spiegelbildes der ursprünglichen Quelle aus. (Diese Theorie wurde von Stewart 1911 vorgeschlagen).[18]
  • Eine Modifikation der Ritz-Tolman-Theorie wurde von Fox (1965) eingeführt. Dieser argumentierte, dass auch die Extinktion (also Absorption, Streuung, und Emission des Lichtes innerhalb eines durchquerten Mediums) berücksichtigt werden muss. In der Luft wäre die Extinktionslänge für sichtbares Licht nur 0,2 cm. Nach dieser Entfernung würde die Lichtgeschwindigkeit nicht mehr konstant zur Quelle, sondern konstant zum Medium sein (wobei Fox selbst Einsteins Relativitätstheorie bevorzugte).[1]

Keines dieser Modelle war jedoch vollständig durchgearbeitet, deswegen wurden sie von der Fachwelt niemals als ernsthafte Alternative zur SRT in Betracht gezogen. Insbesondere wurde ihrer grundlegende Vorhersage, nämlich der Abhängigkeit der Lichtgeschwindigkeit von der Quellengeschwindigkeit, experimentell vielmals widerlegt (s. folgenden Abschnitt).

Experimente

Die kinematische Grundaussage bzw. experimentelle Voraussage der meisten Emissionstheorien, nämlich die Abhängigkeit der Lichtgeschwindigkeit von der Quellengeschwindigkeit, wurde in der Fachwelt in einigen älteren Artikeln bis in die 1960er im Zusammenhang mit Tests der speziellen Relativitätstheorie oder Tests der Lichtkonstanz erwähnt.

Sowohl Emissionstheorie als auch SRT stimmen darin überein, dass kein Ätherwind bzw. kein Einfluss eines bevorzugten Bezugssystems existiert. Das bedeutet, wenn Quelle und Empfänger im selben Inertialsystem ruhen, sagen beide Modelle ein Nullresultat voraus, und sind beispielsweise mit dem negativen Ergebnis des Michelson-Morley-Experiments verträglich.

Unterschiede ergeben sich, wenn Quelle und Empfänger relativ zueinander bewegt sind. Während auch hier gemäß SRT die Lichtgeschwindigkeit in allen Inertialsystemen konstant bleibt, ergibt sich in der Emissionstheorie bei einer Quellengeschwindigkeit von ±v eine Lichtgeschwindigkeit von c±v. Bei Experimenten wird gewöhnlich folgendes Schema benutzt:[19]

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle c'=c\pm kv\,} ,

wo c die Lichtgeschwindigkeit, v die Quellengeschwindigkeit, und c' die resultierende Geschwindigkeit ist; k gibt das Ausmaß der Quellenabhängigkeit an. Bei k=0 ist die Lichtgeschwindigkeit völlig unabhängig von der Quellengeschwindigkeit (wie in der SRT oder dem ruhenden Äther), hingegen bei k=1 ist sie vollständig abhängig von ihr. Werte zwischen 0 und 1 sind auch möglich und repräsentieren eine eingeschränkte Quellenabhängigkeit. Da im Rahmen der aktuellen Messgenauigkeit gezeigt wurde, dass k∼0 ist, gelten die Emissionstheorien als experimentell widerlegt, während die SRT dadurch bestätigt ist.

Michelson-Morley-Experiment

Im Ruhesystem des Interferometers bzw. der Lichtquelle breiten sich die Lichtstrahlen mit konstanter Geschwindigkeit in alle Richtungen aus. Bei einer Armlänge von D (wo D=ct) ergeben sich die Laufzeiten in longitudinaler und transversaler Richtung von je t=D/c und somit für Hin- und Rückweg von

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle T=\frac{2D}{c}} .

Hingegen in einem Inertialsystem, in dem sich die Anordnung mit v bewegt, bekommt das Licht die Geschwindigkeit der Lichtquelle wie bei einem Geschoss gemäß der Galilei-Transformation hinzuaddiert. Die Lichtgeschwindigkeit in longitudinaler Richtung ist c+v und der zurückzulegende Weg D+vt. Bei der Rückkehr bewegt sich der Lichtstrahl mit c-v und der zurückzulegende Weg ist D-vt. Das ergibt eine Laufzeit von:[20]

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle T = \frac{D+vt}{c+v}+\frac{D-vt}{c-v} = \frac{2D}{c}} .

In transversaler Richtung ergibt sich mit dem Satz des Pythagoras: a) wenn D der Laufweg in y-Richtung und vt in x-Richtung ist, ein Laufweg von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sqrt{D^{2}+(vt)^{2}}} , b) wenn c die Geschwindigkeitskomponente in y-Richtung und v in x-Richtung ist, eine Lichtgeschwindigkeit von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sqrt{c^{2}+v^{2}}} . Das ergibt eine Laufzeit von

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle T = 2\sqrt{\frac{D^{2}+(vt)^{2}}{c^{2}+v^{2}}} = \frac{2D}{c}} .

Die Laufzeit T ist also in allen Inertialsystemen gleich, d. h. die Lichtstrahlen breiten sich in allen Systemen konstant relativ zur Lichtquelle aus. Emissionstheorien sind daher bei Verwendung einer stationären Lichtquelle mit dem negativen Ergebnis dieses Experimentes verträglich. Hingegen, wie Tolman ausführte, ergäbe sich beim Modell von Ritz bei Verwendung von Sonnen- bzw. Sternenlicht ein positives Ergebnis.[13]

Widerlegungen

Astronomisch

de Sitters Doppelstern-Argument

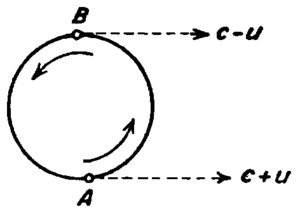
Die unterschiedlichen Geschwindigkeiten, mit denen das Licht je nach Position von Doppelsternen in der Umlaufbahn ausgesandt würde, würde gemäß der Emissionstheorie das auf der Erde empfangene Bild der Umlaufbahnen verzerren. Das heißt, die Sterne verhalten sich scheinbar so, als ob sie den Keplerschen Gesetzen nicht mehr unterworfen wären. Das ist jedoch nicht der Fall, wie Daniel Frost Comstock (1910) und vor allem Willem de Sitter (1913) anführten, wobei Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle k<2\times 10^{-3}} erzielt wurde.[21][22][19] Dieser Einwand betrifft allerdings nicht das Extinktionsmodell von Fox (also Absorption, Streuung, und Emission des Lichtes durch interstellaren Staub, der relativ zur Erde praktisch ruht), wodurch die Lichtstrahlen relativ zur Erde wieder Lichtgeschwindigkeit annehmen.[1] Jedoch Brecher (1977) untersuchte die von Doppelsternen emittierte Röntgenstrahlung, die mit interstellarem Staub kaum wechselwirkt. Dadurch ist die Extinktion nicht groß genug, um das Ergebnis nennenswert zu verfälschen. Auch hier konnten keine Verzerrungen und somit auch keine Abhängigkeit von der Quellengeschwindigkeit festgestellt werden, was Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k < 2\times10^{-9}} entspricht.[23]

Hans Thirring wies 1924 darauf hin, dass „wenn ein Atom auf der Sonne während des Emissionsaktes durch einen thermischen Zusammenstoß eine Änderung der Geschwindigkeitskomponente in der Visionsrichtung erfährt, dann wird der von ihm emittierte Wellenzug von etwa 3 m Gesamtlänge auf dem Wege zur Erde zunächst auf die Länge Null zusammenschrumpfen, wird sich dann gewissermaßen überschlagen und schließlich, mit dem Hinterende voraus, auf eine Gesamtlänge von 500 km auseinander gezogen, beim irdischen Beobachter anlangen, der die Strahlung als Radiowelle von einigen Zentimetern Wellenlänge empfängt. Die ballistische Hypothese wird also in ihrer konsequenten Fassung allein schon durch die Tatsache widerlegt, daß die Sonnenstrahlung ein sichtbares Spektrum mit scharfen Spektrallinien besitzt.“[24]

Terrestrisch

Sadeh (1963) benutzte ein Verfahren zur Flugzeitmessung, um Geschwindigkeitsunterschiede von in entgegengesetzter Richtung sich ausbreitenden Gammastrahlen, die durch Positron-Annihilation entstanden sind, zu messen.[25] Ein anderes Experiment wurde von Alväger et al. (1963) durchgeführt, die die Flugzeit von Gammastrahlen verglichen, die von ruhenden und bewegten Quellen ausgesandt wurden.[26] In beiden Experimenten konnte keine Quellenabhängigkeit festgestellt werden.

Filippas und Fox (1964) waren allerdings der Meinung, dass Sadeh (1963) und Alväger (1963) die Extinktionseffekte nicht ausreichend berücksichtigt haben. Deswegen führten sie ein Experiment mit Gammastrahlen aus dem Zerfall von π0-Mesonen durch, das besonders auf die Vermeidung von Extinktionseffekten ausgerichtet war. Abermals konnte keine Quellenabhängigkeit festgestellt werden.[27]

Alväger et al. (1964) führten nun weitere Tests mit π0-Mesonen durch, die bei einer Geschwindigkeit von 99,9 % der Lichtgeschwindigkeit in Gammastrahlen zerfallen. Die Messung der Flugzeit ergab, dass sich die Photonen weiter mit Lichtgeschwindigkeit bewegten, bei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k =(-3\pm13)\times10^{-5}} . Die Untersuchung der Medien, die bei diesem Experiment von den Photonen durchquert wurden, ergab, dass die Extinktion nicht ausreichend ist, um das Ergebnis nennenswert zu verfälschen.[28]

Inzwischen wurden auch Messungen der Neutrinogeschwindigkeit vorgenommen, wobei als Quelle zerfallende Mesonen mit annähernd Lichtgeschwindigkeit benutzt wurden. Da Neutrinos nur elektroschwach wechselwirken, spielt Extinktion keine Rolle. Es ergaben sich maximale Obergrenzen bei terrestrischen Experiment von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle k\leq10^{-6}} .

Interferometrie

Emissionstheorien widersprechen dem Sagnac-Effekt. Dieser Effekt beruht darauf, dass aufgrund der Rotation eines Interferometers der Weg für einen Strahl länger wird, und für den anderen kürzer. Dies ist aber nur dann möglich, wenn die Lichtgeschwindigkeit unabhängig von der Geschwindigkeit der Quelle ist.[29][30] Auch hier spielt Extinktion keine Rolle, da der Sagnac-Effekt auch im Vakuum auftritt.

Albert A. Michelson (1913)[31] und Quirino Majorana (1918/9)[32][33] führten Experimente mit bewegten Quellen und Spiegeln durch und konnten zeigen, dass in der Luft keine Quellenabhängigkeit vorliegt. Beckmann und Mandics (1965) führten ähnliche Experimente im Hochvakuum durch, wobei eine Quellenabhängigkeit mit k kleiner als 0,09 ausgeschlossen werden konnte. Extinktion konnte zwar nicht völlig, jedoch mit großer Wahrscheinlichkeit ausgeschlossen werden.[34]

Babcock et al. (1964)[35] platzierten rotierende Glasplatten zwischen den Spiegeln eines statischen Interferometers. Wenn die Geschwindigkeit der Glasplatten sich zur Lichtgeschwindigkeit addieren würde, müsste es zu einer messbaren Verschiebung der Interferenzstreifen kommen. Das Ergebnis war jedoch negativ und da das Experiment im Vakuum durchgeführt wurde, spielt Extinktion ebenfalls keine Rolle. Nur die ursprüngliche Theorie von Ritz, wonach die Glasplatten nicht als neue Lichtquellen anzusehen sind, ist mit dem Ergebnis verträglich. Doch gibt es in der Ritzschen Theorie keine Extinktion, wodurch sie im Widerspruch zu allen anderen Experimenten steht, die nur durch Extinktion mit der Emissionstheorie zu vereinbaren sind.

Sonstige Widerlegungen

Die maxwellsche Elektrodynamik und die SRT beruhen auf der Unabhängigkeit der Lichtgeschwindigkeit von der Quelle, und deren Voraussagen sind allesamt mit hoher Präzision experimentell bestätigt worden. Beispielsweise beruhen Emissionstheorien auf der Galilei-Transformation und somit auf einer bezugssystemunabhängigen, absoluten Zeit. Durch den Nachweis der Zeitdilatation wie beispielsweise bei den Ives-Stilwell-Experimenten oder der Zeitdilatation bewegter Teilchen konnte dieses Konzept jedoch ausgeschlossen werden, und die Lorentz-Transformation bestätigt werden. Ebenso wird die damit zusammenhängende Galileische Geschwindigkeitsaddition und auch die Newtonschen Impulsbeziehung durch Tests der relativistischen Energie-Impuls-Beziehung widerlegt, wonach massebehaftete Teilchen nicht auf Lichtgeschwindigkeit und darüber hinaus beschleunigt werden können.

Es wurde bislang keine Emissionstheorie entwickelt, die alle diese experimentellen Resultate mindestens genauso gut erklären könnte, was Voraussetzung ist, damit sie überhaupt als ernsthafte Alternative in Betracht kommen kann. Darüber hinaus wurde die maxwellsche Elektrodynamik zur Quantenelektrodynamik weiterentwickelt, wobei diese als die am genauesten bestätigte Theorie überhaupt gilt – auch hier ist die Lichtgeschwindigkeit unabhängig von der Quellengeschwindigkeit.

Siehe auch

Weblinks

Einzelnachweise

  1. ↑ a b c d Fox, J. G.: Evidence Against Emission Theories. In: American Journal of Physics. 33, Nr. 1, 1965, S. 1-17. doi:10.1119/1.1971219.
  2. ↑ a b Martínez, Alberto A.: Ritz, Einstein, and the Emission Hypothesis. In: Physics in Perspective. 6, Nr. 1, Dezember, S. 4-28. doi:10.1007/s00016-003-0195-6.
  3. ↑ a b Norton, John D.: Einstein's Investigations of Galilean Covariant Electrodynamics prior to 1905. In: Archive for History of Exact Sciences. 59, 2004, S. 45–105. doi:10.1007/s00407-004-0085-6.
  4. ↑ Wolfram Schmitt: Antike und mittelalterliche Theorien über die fünf Sinne. In: Fachprosaforschung – Grenzüberschreitungen. Band 10, 2014, S. 7–18, insbesondere S. 7 f. und 15.
  5. ↑ a b Wuellner, Adolph: Lehrbuch der Experimentalphysik. Ersten Bandes zweite Abtheilung. Optik.. B. G. Teubner, Leipzig 1866, S. 632–635, 699–708.
  6. ↑ Newton, I.: New theory about light and colours. Fritsch, München 1672/1965.
  7. ↑ Newton, I.: Opticks. William Innys, St. Pauls 1704/1730.
  8. ↑ Michell, John: On the means of discovering the distance, magnitude etc. of the fixed stars. In: Philosophical Transactions of the Royal Society. 1784, S. 35-57.
  9. ↑ Laplace, Pierre-Simon: The system of the world (English translation 1809), Band 2. Richard Phillips, London 1796, S. 366-368.
  10. ↑ Soldner, Johann Georg von: Ueber die Ablenkung eines Lichtstrals von seiner geradlinigen Bewegung. In: Berliner Astronomisches yearbuch. 1804, S. 161-172.
  11. ↑ Foucault, Léon: Allgemeine Methode zur Messung der Geschwindigkeit des Lichts in Luft und anderen durchsichtigen Mitteln; relative Geschwindigkeiten des Lichts in Luft und Wasser; Entwurf eines Versuches über die Fortpflanzungs-Geschwindigkeit der strahlenden Wärme;. In: Annalen der Physik. 157, 1850, S. 434.
  12. ↑ Foucault, Léon: Sur les vitesses relatives de la lumière dans l'air et dans l'eau. In: Annales de Chim. et de Phys.. 41, 1854, S. 129.
  13. ↑ a b c Tolman, R.C.: Some Emission Theories of Light. In: Physical Review. 35, Nr. 2, 1912, S. 136–143.
  14. ↑ Kunz, Jakob: An Attempt at an Electromagnetic Emission Theory of Light. In: Physical Review. 3, Nr. 6, 1914, S. 464-475. doi:10.1103/PhysRev.3.464.
  15. ↑ Shankland, R. S.: Conversations with Albert Einstein. In: American Journal of Physics. 31, Nr. 1, 1963, S. 47–57. doi:10.1119/1.1969236.
  16. ↑ Ritz, Walter: Recherches critiques sur l'Électrodynamique Générale Archiviert vom Original am 14. Dezember 2009.  Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/gallica.bnf.fr In: Annales de Chimie et de Physique. 13, 1908, S. 145-275. Abgerufen am 2. Juni 2010.Siehe auch.
  17. ↑ Tolman, R.C.: The Second Postulate of Relativity. In: Physical Review. 31, Nr. 1, 1910, S. 26–40.
  18. ↑ Stewart, Oscar M.: The Second Postulate of Relativity and the Electromagnetic Emission Theory of Light. In: Physical Review. 32, Nr. 4, 1911, S. 418-428.
  19. ↑ a b De Sitter, W.: Über die Genauigkeit, innerhalb welcher die Unabhängigkeit der Lichtgeschwindigkeit von der Bewegung der Quelle behauptet werden kann. In: Physikalische Zeitschrift. 14, 1913, S. 1267.
  20. ↑ Cyrenika, A.A.: Principles of Emission Theory. In: Apeiron. 7. (Es handelt sich hier um eine gegen die anerkannte Mainstreamphysik gerichtete Arbeit. Sie wird hier aber aufgeführt da sie einfache Herleitungen zur Emissionstheorie und MM-Experiment enthält).
  21. ↑ Comstock, D.F.: A Neglected Type of Relativity. In: Physical Review. 30, Nr. 2, 1910, S. 267.
  22. ↑ De Sitter, W.: Ein astronomischer Beweis für die Konstanz der Lichtgeschwindigkeit. In: Physikalische Zeitschrift. 14, 1913, S. 429.
  23. ↑ Brecher, K.: Is the speed of light independent of the velocity of the source. In: Physical Review Letters. 39, 1977, S. 1051-1054. doi:10.1103/PhysRevLett.39.1051.
  24. ↑ Thirring, Hans: Über die empirische Grundlage des Prinzips der Konstanz der Lichtgeschwindigkeit. In: Zeitschrift für Physik. 31, Nr. 1, 1924, S. 133–138.
  25. ↑ Sadeh, D.: Experimental Evidence for the Constancy of the Velocity of Gamma Rays, Using Annihilation in Flight. In: Physical Review Letters. 10, Nr. 7, 1963, S. 271-273. doi:10.1103/PhysRevLett.10.271.
  26. ↑ Alväger, T.; Nilsson, A.; Kjellman, J.: A Direct Terrestrial Test of the Second Postulate of Special Relativity. In: Nature. 197, Nr. 4873, 1963, S. 1191. doi:10.1038/1971191a0.
  27. ↑ T.A. Filippas, Fox, J.G.: Velocity of Gamma Rays from a Moving Source. In: Physical Review. 135, Nr. 4B, 1964, S. B1071-1075.
  28. ↑ Alväger, T.; Farley, F. J. M.; Kjellman, J.; Wallin, L.: Test of the second postulate of special relativity in the GeV region. In: Physics Letters. 12, Nr. 3, 1964, S. 260-262. doi:10.1016/0031-9163(64)91095-9.
  29. ↑ Sagnac, Georges: Sur la preuve de la réalité de l'éther lumineux par l'expérience de l'interférographe tournant. In: Comptes Rendus. 157, 1913, S. 1410–1413.
  30. ↑ Witte, Hans: Sagnac-Effekt und Emissionstheorie. In: Berichte der Deutschen Physikalischen Gesellschaft. 16, 1914, S. 755-756.
  31. ↑ Michelson, A.A.: Effect of Reflection from a Moving Mirror on the Velocity of Light. In: Astrophysical Journal. 37, 1913, S. 190-193.
  32. ↑ Majorana, Q.: On the Second Postulate of the Theory of Relativity: Experimental Demonstration of the Constancy of Velocity of the Light reflected from a Moving Mirror. In: Philosophical Magazine. 35, Nr. 206, 1918, S. 163-174.
  33. ↑ Majorana, Q.: Experimental Demonstration of the Constancy of Velocity of the Light emitted by a Moving Source. In: Philosophical Magazine. 37, Nr. 217, 1919, S. 145-150.
  34. ↑ P. Beckmann, Mandics, P.: Test of the Constancy of the Velocity of Electromagnetic Radiation in High Vacuum. In: Radio Science Journal of Research NBS/USNC-URSI. 69D, Nr. 4, 1965, S. 623-628.
  35. ↑ Babcock, G. C.; Bergman, T. G.: Determination of the Constancy of the Speed of Light. In: Journal of the Optical Society of America. 54, Nr. 2, 1964, S. 147-150. doi:10.1364/JOSA.54.000147.
Abgerufen von „https://de.wikiup.org/index.php?title=Korpuskeltheorie&oldid=225423975“