McShane-Identität

In der Mathematik ist die McShane-Identität eine Aussage über die Längen kürzester Linien (geschlossener Geodäten) auf hyperbolischen Flächen.

Sie ist unter anderem bemerkenswert, weil sie nicht von der hyperbolischen Metrik abhängt (obwohl Flächen einen hoch-dimensionalen Modulraum hyperbolischer Metriken besitzen), sowie wegen der Anwendungen ihrer verschiedenen Verallgemeinerungen in der höheren Teichmüller-Theorie.

McShane-Identität für hyperbolische Flächen

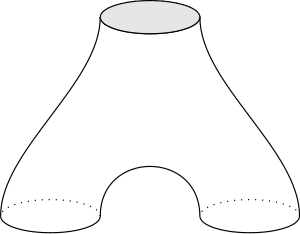
Torus mit Loch

(McShane 1991): Für die einfachen geschlossenen Geodäten in einem hyperbolischen Torus mit Loch gilt die Identität

$\sum _{\gamma }{\frac {1}{1+e^{l(\gamma )}}}={\frac {1}{2}}$,

wobei über alle geschlossenen einfachen Geodäten $\gamma$ summiert wird und $l(\gamma )$ die Länge der geschlossenen Geodäte bezeichnet.

Beliebige hyperbolische Flächen

Eine Hose wird von 3 geschlossenen Kurven berandet.

(McShane 1998): Für eine hyperbolische Fläche mit einer Spitze gilt

$\sum _{\alpha ,\beta }{\frac {1}{1+e^{\frac {l(\alpha )+l(\beta )}{2}}}}={\frac {1}{2}}$,

wobei über alle diejenigen Paare geschlossener einfacher Geodäten summiert wird, die gemeinsam mit der Spitze eine Hose beranden.

Mirzakhanis Verallgemeinerung

Die folgende von Mirzakhani bewiesene Formel diente als Ausgangspunkt für ihre Berechnung des Weil-Petersson-Volumens der Modulräume hyperbolischer Metriken auf (berandeten) Flächen.

Für eine hyperbolische Fläche, deren Randkomponenten $\beta _{1},\beta _{2},\ldots ,\beta _{n}$ geschlossene Geodäten der Längen $L_{1},L_{2},\ldots ,L_{n}$ sind, gilt:

$\sum _{\{\gamma _{1},\gamma _{2}\}}{\mathfrak {D}}(L_{1},l(\gamma _{1}),l(\gamma _{2}))+\sum _{i=2}^{n}\sum _{\gamma }{\mathfrak {R}}(L_{1},L_{i},l(\gamma ))=L_{1}$.

Hierbei ist die erste Summe über alle ungeordneten Paare geschlossener einfacher Geodäten $\{\gamma _{1},\gamma _{2}\}$, die mit $\beta _{1}$ eine Hose beranden, die zweite Summe ist über alle geschlossenen einfachen Geodäten $\gamma$, die mit $\beta _{1},\beta _{i}$ eine Hose beranden. Die Funktionen ${\mathfrak {D}},{\mathfrak {R}}\colon \mathbb {R} _{+}^{3}\to \mathbb {R} _{+}$ werden durch die Geometrie der Hosen definiert, eine explizite Formel ist

${\mathfrak {D}}(x,y,z)=2\log \left({\frac {e^{\frac {x}{2}}+e^{\frac {y+z}{2}}}{e^{\frac {-x}{2}}+e^{\frac {y+z}{2}}}}\right),{\mathfrak {R}}(x,y,z)=x-\log \left({\frac {\cosh({\frac {y}{2}})+\cosh({\frac {x+z}{2}})}{\cosh({\frac {y}{2}})+\cosh({\frac {x-z}{2}})}}\right).$

Andere Lie-Gruppen

Für eine quasifuchssche hyperbolische 3-Mannigfaltigkeit $M$ homotopieäquivalent zum Torus mit Loch (also eine quasifuchssche Darstellung $\rho \colon F_{2}\to SL(2,\mathbb {C} )$ der freien Gruppe vom Rang 2) gilt ebenfalls die Identität

$\sum _{\gamma }{\frac {1}{1+e^{l(\gamma )}}}={\frac {1}{2}}$,

wobei über alle geschlossenen einfachen Geodäten in $M=\rho (F_{2})\backslash \mathbb {H} ^{3}$ summiert wird. (Bowditch 1997)

Andere Verallgemeinerungen der McShane-Identität existieren für eine Reihe weiterer Darstellungen von Flächengruppen in $SL(2,\mathbb {C} )$, zum Beispiel für quasifuchssche Darstellungen freier Gruppen (Akiyoshi-Miyachi-Sakuma), und auch für Hitchin-Darstellungen von Flächengruppen und freien Gruppen in $SL(n,\mathbb {R} )$ (Labourie-McShane).

Literatur

• McShane, Gregory: A remarkable identity for lengths of curves, Ph.D. thesis, Univ. Warwick, Coventry, (1991).
• Bowditch, B. H.: A proof of McShane's identity via Markoff triples. Bull. London Math. Soc. 28 (1996), no. 1, 73–78.
• Bowditch, B. H.: A variation of McShane's identity for once-punctured torus bundles. Topology 36 (1997), no. 2, 325–334.
• McShane, Gregory: Simple geodesics and a series constant over Teichmuller space. Invent. Math. 132 (1998), no. 3, 607–632.
• Akiyoshi, Hirotaka; Miyachi, Hideki; Sakuma, Makoto: Variations of McShane's identity for punctured surface groups. Spaces of Kleinian groups, 151–185, London Math. Soc. Lecture Note Ser., 329, Cambridge Univ. Press, Cambridge, 2006.
• Mirzakhani, Maryam: Simple geodesics and Weil-Petersson volumes of moduli spaces of bordered Riemann surfaces. Invent. Math. 167 (2007), no. 1, 179–222.
• Tan, Ser Peow; Wong, Yan Loi; Zhang, Ying: McShane's identity for classical Schottky groups. Pacific J. Math. 237 (2008), no. 1, 183–200.
• Labourie, François; McShane, Gregory: Cross ratios and identities for higher Teichmüller-Thurston theory. Duke Math. J. 149 (2009), no. 2, 279–345.

Weblinks

• Bridgeman, Martin; Tan, Ser Peow: Identities on hyperbolic manifolds