Multiplikatives magisches Quadrat
Ein multiplikatives magisches Quadrat[1] ist eine Variante des allgemeinen magischen Quadrats. Es ist ein spezielles Zahlenquadrat, bei dem das Produkt der Zahlen jeder Zeile, jeder Spalte und jeder Diagonalen stets gleich ist.
Eigenschaften
Alle Eigenschaften, die sich bei den additiven magischen Quadraten auf Summen beziehen, lassen sich analog auf Produkte übertragen.
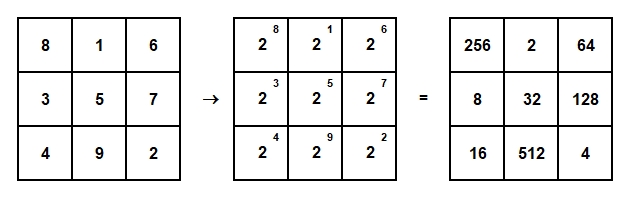
Die Umwandlung von magischen Summenquadraten zu magischen Produktquadraten beruht auf dem ersten Potenzgesetz:
Potenzen mit gleicher Basis werden multipliziert, indem man ihre Exponenten addiert.
Beispiel Dreierquadrat:
Die 8 Produkte der Zahlen jeder Zeile, Spalte und Diagonalen ergeben jeweils das magische Produkt 32.768.
Beispiel Duererquadrat:
Beim magischen Quadrat von Albrecht Dürer werden sogar alle 86 Summenkombinationen der magischen Zahl in analoger Weise zu 86 Produktkombinationen der magischen Zahl.
Die 10 Produkte der Zahlen jeder Zeile, Spalte und Diagonalen und der weiteren 76 Kombinationen ergeben jeweils das magische Produkt 17.179.869.184.