Rösselsprung-Quadrat
Ein Rösselsprung-Quadrat ist ein achtreihiges Zahlenquadrat, das aus den natürlichen Zahlen 1 bis 64 besteht und folgende Besonderheit aufweist:
Ein Springer auf dem Ausgangsfeld mit der 1 kann regelkonform so gezogen werden, dass er der Reihe nach alle Zahlen bis 64 genau einmal erreicht. Eine solche Abfolge von Springerbewegungen wird in der Schach-Sprache auch Springertour genannt. Von einer geschlossenen Springertour spricht man, wenn mit einem zusätzlichen Sprung vom letzten Feld der Springertour das Anfangsfeld wieder erreicht werden kann.
Veröffentlichungen
Bereits im Mittelalter wurden die Existenz und die Art von Springertouren exemplarisch erörtert. Der Schweizer Mathematiker und Physiker Leonhard Euler analysierte von 1757 bis 1759 Springertouren erstmals detailliert.[1]
1838 beschrieb der Nürnberger Mathematiklehrer Christoph Wilhelm Zuckermandel Regeln zur Bildung von Zauberquadraten, zusammen mit einer Anweisung über den Rösselsprung.[2]
Der ehemalige russische Schachmeister Carl Ferdinand Jänisch veröffentlichte 1859 einen Beitrag über die symmetrische magische Springertour im New Yorker Schachmagazin The Chess Monthly.[3]
Magische und semimagische Rösselsprung-Quadrate
Ist das Rösselsprung-Quadrat ein magisches Quadrat, bzw. semimagisches Quadrat, so handelt es sich um eine sogenannte magische Springertour, bzw. semimagische Springertour.[4]
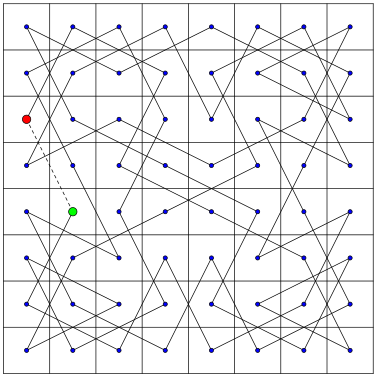
Beispiel
Das folgende semimagische Rösselsprung-Quadrat mit der magischen Zahl 260, bei dem zwar die Zeilen- und Spaltensummen gleich sind, aber nicht mit den beiden Diagonalensummen übereinstimmen, stellt eine geschlossene semimagische Springertour dar. Vom Anfangsfeld 1 (grün) startend kann ein Springer der Reihe nach alle Zahlen bis 64 genau einmal und mit einem Folgesprung vom letzten Feld (rot) wieder das Anfangsfeld erreichen.
Semimagisches Rösselsprung-Quadrat
Geschlossene semimagische Springertour
Siehe auch
Weblinks
- Klaus Pommerening: Kryptologie - Rösselsprung, Johannes Gutenberg-Universität Mainz, abgerufen am 11. September 2022
- W. Ahrens: Mathematische Unterhaltungen und Spiele, B. G. Teubner Verlag, Leipzig 1901
- Eric Weisstein: There are no Magic Knight’s Tour on the Chessboard, Wolfram MathWorld
- Andreas Kühne, Christina Reiher: Rösselsprung aus magischesquadrat.de, abgerufen am 11. September 2022
- Springerproblem, Rösselsprung, Rösselsprungrätsel aus schach-chess.com, abgerufen am 11. September 2022
- Magische Quadrate im Schach Knowledgebase von Gerald Allerstorfer, veröffentlicht am 18. März 2018, abgerufen am 15. September 2022
- Andreas Stiller: Magisches Springer-Problem gelöst heise online vom 6. September 2003, abgerufen am 15. September 2022
Einzelnachweise
- ↑ Leonhard Euler: Solution d'une Question Curieuse qui ne Paroit Soumise a Aucune Analyse. Mémoires de l'Académie des Sciences de Berlin, pages 310–337, 1759
- ↑ Christoph Wilhelm Zuckermandel: Regeln, nach denen alle Zauberquadrate gebildet werden können, Nürnberg 1838
- ↑ Carl Friedrich Andreyevich Jänisch: La solution la plus parfaite du Problème du Cavalier, The Chess Monthly, Band 3, April/Mai/Juni 1859, Seiten 110–115, 146–151 und 176–179
- ↑ Torsten Bosse, Andreas Griewank, Lutz Lehmann, Daniel Schlagk: Die magische Quadratur des Superhirns aus researchgate.net, abgerufen am 11. September 2022
