Satz von König (Graphentheorie)

Der Satz von König ist ein mathematischer Satz aus der Graphentheorie, der für bipartite Graphen einen Zusammenhang zwischen einer größten Paarung und einer minimalen Knotenüberdeckung aufzeigt. Er lautet:

In einem bipartiten Graphen ist die Größe einer größten Paarung gleich der Größe einer kleinsten Knotenüberdeckung.

Der Satz ist nach dem ungarischen Mathematiker Dénes Kőnig benannt, der ihn 1931 bewiesen hat. Unabhängig von König hat der Mathematiker Jenő Egerváry, ebenfalls im Jahr 1931 , eine allgemeinere Formulierung des Theorems für gewichtete Graphen bewiesen. Deshalb wird der Satz gelegentlich auch als Satz von König und Egerváry bezeichnet.

Er lässt sich auch auf unendliche Graphen übertragen, wie schon Paul Erdős vermutete und wie Ron Aharoni bewies.

Beispiel

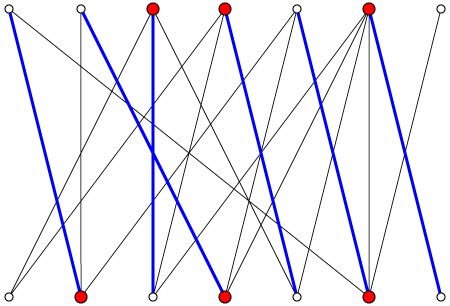
Ein Beispiel eines bipartiten Graphen, mit größter Paarung (blau) und minimaler Knotenüberdeckung (rot):

Algorithmus

Dieser Algorithmus beschreibt wie man aus einer größten Paarung die minimale Knotenüberdeckung erhält. Eine größte Paarung kann beispielsweise mit dem Algorithmus von Hopcroft und Karp berechnet werden. Die beiden Knotenmengen des bipartiten Graphen werden in Folge mit $O$ (oben) und $U$ (unten) bezeichnet.

1. Eine größte Paarung berechnen.
2. Alle nicht in der Paarung enthaltenen Knoten aus $O$ werden in $T$ eingefügt.
3. Auf nicht in der Paarung enthaltenen Kanten gehen wir von diesen Knoten nach $U$. Alle besuchten Knoten werden in $T$ eingefügt.
4. Von den so erreichten Knoten in $U$ gehen wir auf in der Paarung enthaltenen Kanten wieder nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle O} . Alle besuchten Knoten werden in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle T} eingefügt.
5. Wiederhole die beiden vorherigen Schritte, solange bis keine neuen Knoten mehr in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle T} eingefügt werden.
6. Die minimale Knotenüberdeckung ergibt sich aus Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (O \setminus T) \cup (U \cap T)}

Variante für gewichtete Graphen

Unabhängig von König hat der Mathematiker Jenő Egerváry eine Variante des Theorems für gewichtete Graphen bewiesen. Hier betrachtet man bipartite Graphen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle G=(V=A\cup B,E)} mit einer Gewichtsfunktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d \colon E \to \mathbb{N}} die jeder Kante im Graphen eine nichtnegative ganze Zahl zuordnet. Eine gewichtete Knotenüberdeckung von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d} ist eine Funktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \pi \colon V \to \mathbb{N}} die jedem Knoten im Graphen eine nichtnegative ganze Zahl zuordnet, sodass $\pi (u)+\pi (v)\geq d(\{u,v\})$ für alle Kanten $\{u,v\}\in E$ gilt. Das Gewicht von $\pi$ is durch $\sum _{v\in V}\pi (v)$ gegeben. Der Satz lautet dann wie folgt:

In einem vollständigen bipartiten Graphen $G=(V=A\cup B,E)$ mit $|A|=|B|$ und einer Gewichtsfunktion $d\colon E\to \mathbb {N}$, entspricht das maximale Gewicht einer Paarung dem minimalen Gewicht einer gewichteten Knotenüberdeckung von $d$.

Weblinks

Wikiversity: Ein Beweis des Satzes von König im Rahmen eines Kurses zur diskreten Mathematik – Kursmaterialien

• Eric W. Weisstein: König-Egeváry Theorem. In: MathWorld (englisch).
• Beweis zum Satz von König (PDF; 286 kB)