Trachtenberg-System

Das Trachtenberg-System, auch Trachtenberg-Schnellrechenmethode genannt, ist ein System zum schnellen Kopfrechnen. Es besteht aus mehreren leicht zu erkennenden Operationen, die es erlauben, arithmetische Rechnungen schnell durchzuführen. Entwickelt wurde das System vom russisch-jüdischen Ingenieur Jakow Trachtenberg, der das System in einem Konzentrationslager der Nationalsozialisten erfand, während er dort einsaß. Die wichtigsten Algorithmen sind die für das allgemeine Multiplizieren, das Dividieren und das Addieren. Außerdem enthält das Trachtenberg-System einige spezielle Methoden für die Fälle der Multiplikation von kleinen Zahlen zwischen fünf und dreizehn.

Die Methode zur Addition enthält ein effektives Verfahren zur Überprüfung von Berechnungen, welches auch auf die Multiplikation angewandt werden kann.

Allgemeines Multiplizieren

Das Verfahren für das allgemeine Multiplizieren ist ein Verfahren, um Multiplikationen $a\times b$ mit einem geringen Aufwand durchführen zu können; das heißt, sich so wenige Zwischenergebnisse wie möglich merken zu müssen. Das wird erreicht mithilfe der Feststellung, dass die Endziffer der Multiplikation bestimmt ist von den letzten Ziffern der Faktoren. Diese wird als Zwischenergebnis festgehalten. Um die vorletzte Ziffer zu finden, braucht man alles, was diese Ziffer beeinflusst: Das Zwischenergebnis, die letzte Ziffer von $a$ mal die vorletzte Ziffer von $b$, sowie die vorletzte Ziffer von $a$ mal die letzte Ziffer von $b$. Diese Berechnung wird durchgeführt und wir haben ein Zwischenergebnis, dessen letzte beide Ziffern korrekt sind.

Im Allgemeinen, für jede Position $n$ im Endergebnis, haben wir für alle $i$:

$a\ (\mathrm {Ziffer\ bei\ } i)\times \ b\ (\mathrm {Ziffer\ bei\ } (n-i)).$

Man kann diesen Algorithmus erlernen und dann vierstellige Zahlen im Kopf multiplizieren, nur mit dem Niederschreiben des Endergebnisses. Man fängt rechts an und endet mit der linkesten Ziffer.

Trachtenberg definierte diesen Algorithmus mit einer Art paarweiser Multiplikation, bei der zwei Ziffern multipliziert werden mit einer anderen Ziffer, nur mit Beibehalten der mittleren Ziffer des Ergebnisses. Beim Anwenden dieses Algorithmus mit der paarweisen Multiplikation wird man immer weniger Zwischenergebnisse festhalten müssen.

Beispiel: $123456\times 789$

Um die erste Ziffer des Ergebnisses zu finden:

Die Einer von $9\times 6=4.$

Um die zweite Ziffer des Ergebnisses zu finden, fängt man bei der zweiten Ziffer des Multiplikanden an:

Die Einer von $9\times 5$ plus die Zehner von $9\times 6$ plus

die Einer von $8\times 6$.

$5+5+8=18$.

Die zweite Ziffer ist $8$ und $1$ gemerkt für die dritte Ziffer.

Um die dritte Ziffer zu finden, beginnt man bei der dritten Ziffer des Multiplikanden:

Die Einer von $9\times 4$ plus die Zehner von $9\times 5$ plus

die Einer von $8\times 5$ plus die Zehner von $8\times 6$ plus

die Einer von $7\times 6$.

$1+6+4+4+0+2=17$.

Die dritte Ziffer der Antwort ist $7$ und $1$ gemerkt für die vierte Ziffer.

Um die vierte Ziffer zu finden, beginnt man bei der vierten Ziffer des Multiplikanden:

Die Einer von $9\times 3$ plus die Zehner von $9\times 4$ plus

die Einer von $8\times 4$ plus die Zehner von $8\times 5$ plus

die Einer von $7\times 5$ plus die Zehner von $7\times 6$.

$1+7+3+2+4+5+4=26$.

Die vierte Ziffer der Antwort ist $6$ und $2$ gemerkt für die fünfte Ziffer.

Mit der gleichen Methode für die restlichen Zahlen fortfahren.

Zwei-Finger Methode

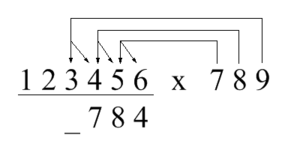
Trachtenberg nannte dies die Zwei-Finger Methode. Die Berechnungen, um die vierte Ziffer aus obigem Beispiel zu finden, sind anhand der Grafik rechts gut zu erkennen:

Der Pfeil von der neun wird immer auf die Ziffer des Multiplikanden direkt über der Antwort zeigen, für die Sie den Wert berechnen möchten. Die anderen Pfeile zeigen immer eins nach rechts. Der vertikale Pfeil zeigt die Ziffer, von der wir die Einer brauchen, der schräge Pfeil auf diejenige Ziffer, von der wir die Zehner brauchen. Wenn ein Pfeil auf ein Feld mit keiner Zahl zeigt, muss hierfür keine Berechnung vorgenommen werden. Mit der Berechnung einer Zahl rutscht die Ansammlung an Pfeilen immer um eine Einheit nach links solange, bis alle Pfeile an vorangestellte Nullen zeigen.

Allgemeine Division

Dividiert wird im Trachtenberg-System sehr ähnlich der Trachtenberg'schen Multiplikation, aber mit Subtraktion statt Addition.

Literatur

• Trachtenberg, J. (1960): The Trachtenberg Speed System of Basic Mathematics. Doubleday and Company, Inc., Garden City, NY, US
• Э. Катлер, Р. Мак-Шейн: Система быстрого счёта по Трахтенбергу, 1967.
• Rushan Ziatdinov, Sajid Musa: Rapid mental computation system as a tool for algorithmic thinking of elementary school students development. European Researcher 25(7): 1105-1110, 2012.

Weblinks

• Halber Nachbar