Wavelet-Paket-Transformation

Die Wavelet-Paket-Transformation ist eine Erweiterung der schnellen Wavelet-Transformation (FWT) und dient wie diese in der digitalen Signalverarbeitung der Analyse und Kompression digitaler Signale. In der FWT wird ein zeitdiskretes Eingangssignal mit einer Abtastrate F mittels einer Wavelet-Filterbank (z. B. der Daubechies-Wavelets) in einen Tiefpasskanal L und einen Bandpasskanal H mit halber Abtastrate F/2 aufgespalten und dieses Vorgehen für den Tiefpasskanal rekursiv wiederholt. So entstehen im darauffolgenden Schritt aus dem Kanal L die Kanäle LL und LH mit Abtastrate F/4, aus dem Kanal LL im nächsten Schritt die Kanäle LLL und LLH und so weiter.

Bei der Wavelet-Paket-Transformation werden nun auch die Bandpasskanäle aufgespalten, sodass im zweiten Rekursionsschritt nicht nur LL und LH, sondern auch die Kanäle HL und HH entstehen. Im dritten Schritt entstehen so acht Teilkanäle usw. Die Teilkanäle des Ergebnisses und der Zwischenschritte können in einem binären Baum angeordnet werden.

Diese Transformation kann dazu dienen, aus einer 2-Kanal-DWT wie z. B. den Daubechies-Wavelets eine M-Kanal-DWT zu erhalten, wobei M eine Potenz von zwei ist, der Exponent wird Tiefe des Paket-Baums genannt. Dieses Verfahren wird in der Breitbanddatenübertragung als DWT-OFDM bzw. DWPT-OFDM als Alternative zur schnellen Fourier-Transformation in der FFT-OFDM angewandt.

Hat die zugrundeliegende Wavelet-Transformation eine Skalierungsfunktion φ mit Tiefpassfilter Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a(Z)} (L-Kanal) und Bandpassfilter Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b(Z)} (H-Kanal), so ergeben sich die Wavelets der Kanäle zu

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \psi_\text{L}(x/2) &:= a(S)\phi(x) = \sum_n a_n\phi(x-n) = \phi(x/2)\, ,\\ \psi_\text{H}(x/2) &:= b(S)\phi(x) = \sum_n b_n\phi(x-n) = \psi(x/2)\, , \end{align}}

wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S} der Operator der Verschiebung (shift) um 1 in Richtung wachsender Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} -Werte ist, d. h. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (Sf)(x)=f(x-1)} . Potenzen von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S} sind dann Verschiebungen um den Exponenten der Potenz, Laurent-Polynome in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle S} entsprechen den jeweiligen Linearkombinationen der verschobenen Funktionen.

Bis hier sind die Funktionen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \phi} und $\psi$ identisch mit den in der FWT auftretenden. Im zweiten Schritt ergeben sich neue Funktionen

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \psi_\text{LL}(x/4)&:=a(S^2)a(S)\phi(x)=\phi(x/4),\\ \psi_\text{LH}(x/4)&:=b(S^2)a(S)\phi(x)=\psi(x/4),\\ \psi_\text{HL}(x/4)&:=a(S^2)b(S)\phi(x)\, ,\\ \psi_\text{HH}(x/4)&:=b(S^2)b(S)\phi(x)\, . \end{align}}

Ist das Spektrum von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \phi(x)=\psi_\text{LL}(x)} nahezu optimal auf das Basisband Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left[0,1/2\right]} beschränkt und sind Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle b} gute frequenzselektive digitale Filter für die sich 1-periodisch wiederholenden Intervalle Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left[-1/4,1/4\right]} bzw. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left[1/4,3/4\right]} , so wird das Spektrum von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \psi(x)=\psi_\text{LH}(x)} auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left[1/2,1\right]} konzentriert sein, das von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \psi_\text{LH}(x)} auf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (\left[-1/2,1/2\right]\cup\left[3/2,5/2\right])\cap\left[1,3\right]\cap\left[0,2\right]=\left[3/2,2\right]} , das von $\psi _{\text{HH}}(x)$ auf Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle (\left[1/2,3/2\right]\cup \left[5/2,7/2\right])\cap \left[1,3\right]\cap \left[0,2\right]=\left[1,3/2\right]} , d. h. die Frequenzbänder der Kanäle sind in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left[0,2\right]} , jedes mit Breite 1/2, in der Reihenfolge LL, LH, HH, HL angeordnet.

Im dritten Schritt dann

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \psi_\text{LLL}(x/8)&:=a(S^4)a(S^2)a(S)\phi(x)=\phi(x/8),\\ \psi_\text{LLH}(x/8)&:=b(S^4)a(S^2)a(S)\phi(x)=\psi(x/8)\, ,\\ \psi_\text{LHL}(x/8)&:=a(S^4)b(S^2)a(S)\phi(x)\, ,\\ \psi_\text{LHH}(x/8)&:=b(S^4)b(S^2)a(S)\phi(x)\, ,\\ \psi_\text{HLL}(x/8)&:=a(S^4)a(S^2)b(S)\phi(x)\, ,\\ \psi_\text{HLH}(x/8)&:=b(S^4)a(S^2)b(S)\phi(x)\, ,\\ \psi_\text{HHL}(x/8)&:=a(S^4)b(S^2)b(S)\phi(x)\, ,\\ \psi_\text{HHH}(x/8)&:=b(S^4)b(S^2)b(S)\phi(x)\, . \end{align}}

usw.

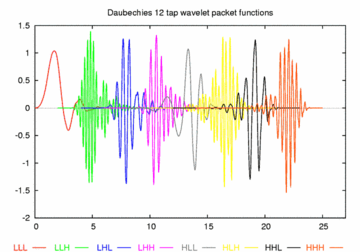
In der folgenden Grafik wurden die Wavelets der dritten Stufe dargestellt, die sich aus dem Daubechies-12-Tap-Wavelet D12 ergeben, der Übersichtlichkeit halber ganzzahlig verschoben. Daneben die Amplituden der Fourier-Transformierten der einzelnen Wavelets. Man kann aus den Spektren im Amplitudenbereich oberhalb 0,7 die Aufteilung des Frequenzbandes Fehler beim Parsen (Konvertierungsfehler. Der Server („https://wikimedia.org/api/rest_“) hat berichtet: „Cannot get mml. Server problem.“): {\displaystyle \left[0,4\right]} in die acht Teilkanäle der Breite 1/2 mit der Reihenfolge LLL, HLL, HHL, LHL, LHH, HHH, HLH, LLH ablesen. Dies entspricht einer Variante eines Gray-Codes.

Weblinks

• Wavelet Packet Modulation for Wireless Communications (PDF, englisch; 677 kB)
• Implementierung der Wavelet-Paket-Transformation in Java (englisch; Softwareprojekt)