Benutzer:Zumthie/Mathematisches
| Babel: | ||
|---|---|---|
| ||
| Benutzer nach Sprache |
Mersenne-Primzahlen
| Die Mersenne-Primzahl ist eine Primzahl, die ausschließlich mit der Binärziffer "1" geschrieben wird. | |||||||||
| binär | 11 | 111 | 11111 | 1111111 | 1111111111111 | 11111111111111111 | 1111111111111111111 | 1111111111111111111111111111111 | … |
|---|---|---|---|---|---|---|---|---|---|
| potenz | 22-1 | 23-1 | 25-1 | 27-1 | 213-1 | 217-1 | 219-1 | 231-1 | … |
| dezimal | 3 | 7 | 31 | 127 | 8191 | 131071 | 524287 | 2147483647 | … |
| Die wichtigste Eigenschaft einer Mersenne-Primzahl: „Die Anzahl der Binärziffern muss eine Primzahl sein.“ | |||||||||
Die Mersennezahl ist eine Binärzahl, die gerade aus Einsen besteht (Zahlenpalindrom). Bei Mersenne-Primzahlen (Primzahlpalindrom) ist also die Anzahl der Einsen selbst eine Primzahl. Dies ist eine notwendige aber nicht hinreichende Voraussetzung!
Teilbarkeit von Repunits
Repunits sind Zahlen, die nur mit der Ziffer Eins geschrieben werden. Jede Repunit deren Ziffernanzahl keine Primzahl ist, ist durch jede Repunit teilbar die soviel Ziffern enthält wie ein Teiler der Ziffernanzahl des Dividenden. Beispiel: Die Zahl 111111111111 ist eine Repunit und enthält 12 Ziffern. 12 ist teilbar durch 2, 3, 4 und durch 6, deswegen ist die Zahl teilbar durch die Repunits 11, 111, 1111 und auch durch 111111. Das Ergebnis einer solchen Division ist immer eine Palindromzahl, die nur aus den Ziffern Eins und Null besteht. Das Ergebnis sieht in jedem polyadischen Zahlensystem gleich aus, obwohl diese Zahlen ganz unterschiedliche Werte darstellen.
Repunit Basis durch Teilerrepunit Basis:
| RepunitBasis | TeilerrepunitBasis | QuotientBasis | Quotientdezimal |
|---|---|---|---|
| 1111111111112 | 112 | 101010101012 | 1365dezimal |
| 1111111111112 | 1112 | 10010010012 | 585dezimal |
| 1111111111112 | 11112 | 1000100012 | 273dezimal |
| 1111111111112 | 1111112 | 10000012 | 65dezimal |
Verallgemeinerung:
Repunit b durch Teilerrepunit b
Wobei b Element der Ganzen Zahlen >1:
| Repunitb | Teilerrepunitb | Quotientb |
|---|---|---|
| 11 11 11 11 11 11b | 11b | 1 01 01 01 01 01b |
| 111 111 111 111b | 111b | 1 001 001 001b |
| 1111 1111 1111b | 1111b | 1 0001 0001b |
| 111111 111111b | 111111b | 1 000001b |
Fazit:
Jede als Repunit darstellbare Zahl ist teilbar (keine Primzahl), wenn die Anzahl ihrer Ziffern teilbar ist!
Repunits
Repunits sind eine Teilmenge der Repdigits. Unter den Repdigits können nur bei den Repunits Primzahlen sein.
Die ersten Zahlen dieser Art, die aus diesem Grund keine Primzahlen sein können sind:
- 15 (1111 Basis 2)
- 40 (1111 Basis 3)
- 63 (111111 Basis 2)
- 85 (1111 Basis 4)
- 156 (1111 Basis 5)
- 255 (11111111 Basis 2)
- 259 (1111 Basis 6)
- 364 (111111 Basis 3)
- 400 (1111 Basis 7)
- 511 (111111111 Basis 2)
...
Umgekehrt ist jede Primzahl p>2 in dem Stellenwertsystem mit der Basis p-1 eine 2-stellige Repunit. Besonders interessant sind aber die Repunits mit mehr als 2 Stellen die Primzahlen sind. In der Folge A085104 in OEIS sind diese Art Primzahlen aufgeführt.
Pythonprogramm Lucas-Lehmer-Test
Mit dem Lucas-Lehmer-Test läßt sich sehr schnell prüfen ob eine Mersennezahl auch eine Mersenne-Primzahl ist. Mit dem hier gezeigten Pythonprogramm können Mersennezahlen überprüft werden, wobei die Berechnungen bis zur 20ten Mersenne-Primzahl jeweils nur wenige Sekunden dauern. (Download: Portable Python 2.6.1)
#!/Lucas-Lehmer-Test für Python 2.6.1
print 'Lucas-Lehmer-Test (Mersenne-Zahlen)'
p = int(raw_input ('Exponent p von 2^p-1'))
m=2**p-1
print 'm = 2 ^',p,'- 1 =',m
s=4
for i in range (2,p):
s=(s*s-2)%m
print 'ist',
if s==0:
print 'eine',
else:
print 'keine',
print 'Mersenne-Primzahl'
Exponenten p (2p-1) der ersten 20 Mersenne-Primzahlen
- 2
- 3
- 5
- 7
- 13
- 17
- 19
- 31
- 61
- 89
- 107
- 127
- 521
- 607
- 1279
- 2203
- 2281
- 3217
- 4253
- 4423
Repunits2, besondere Palindromzahlen
Quadrate der Repunits mit b-1 Ziffern in der Basis b ergeben unvollständige Palindromzahlen der Form 123..(b-1)..321 in der entsprechenden Basis b.
Beispiel: 111112(6)=123454321(6)=15552(10)=2418025(10)
Die dezimalen Werte dieser Repunits sind in der Folge A060072 in OEIS aufgeführt.
Basis 2 Repunits2 (Mersennezahlen2)
(2n-1)2 = 2(n+1)(2(n-1)-1)+1
Repunits und Palindrome in Dreieckszahlen
Unter den Dreieckszahlen sind besondere Palindromzahlen aufgeführt. Die n-ten Dreieckszahlen bei denen n Repunits mit einer geraden Anzahl von Stellen (vollständige Palindromzahlen) sind, scheinen vollständige palindromische Dreieckszahlen zu indizieren die eine auffällige Ziffernfolge aufweisen. Tatsächlich lassen sich n-te palindromische Dreieckszahlen in Stellenwertsystemen mit gerader Basis > 2 konstruieren.
(Folge A000217 in OEIS) und Liste der Dreieckszahlen
Repunit 11Basis n-te palindromische DreieckszahlBasis:
| nBasis | DreieckszahlBasis | ndezimal | Dreieckszahldezimal |
|---|---|---|---|
| 114 | 334 | 5dezimal | 15dezimal |
| 116 | 446 | 7dezimal | 28dezimal |
| 118 | 558 | 9dezimal | 45dezimal |
| 1110 | 6610 | 11dezimal | 66dezimal |
| 1112 | 7712 | 13dezimal | 91dezimal |
| 1114 | 8814 | 15dezimal | 120dezimal |
| ... | ... | ... | ... |
- (Siehe hierzu auch: A000384)
Repunit 1111Basis n-te palindromische DreieckszahlBasis:
| nBasis | DreieckszahlBasis | ndezimal | Dreieckszahldezimal |
|---|---|---|---|
| 11114 | - | 85dezimal | - |
| 11116 | 4155146 | 259dezimal | 33670dezimal |
| 11118 | 5166158 | 585dezimal | 171405dezimal |
| 111110 | 61771610 | 1111dezimal | 617716dezimal |
| 111112 | 71881712 | 1885dezimal | 1777555dezimal |
| 111114 | 81991814 | 2955dezimal | 4367490dezimal |
| ... | ... | ... | ... |
Repunit 111111Basis n-te palindromische DreieckszahlBasis:
| nBasis | DreieckszahlBasis | ndezimal | Dreieckszahldezimal |
|---|---|---|---|
| 1111114 | - | 1365dezimal | - |
| 1111116 | - | 9331dezimal | - |
| 1111118 | 51627726158 | 37449dezimal | 701232525dezimal |
| 11111110 | 617288271610 | 111111dezimal | 6172882716dezimal |
| 11111112 | 718299281712 | 271453dezimal | 36843501331dezimal |
| 11111114 | 8192AA291814 | 579195dezimal | 167733713610dezimal |
| ... | ... | ... | ... |
Je größer die Basis eines Stellenwertsystems gewählt wird, desto mehr palindromische Dreieckszahlen lassen sich konstruieren!
Die größten hexadezimalen palindromischen Dreieckszahlen dieser Art sind:
RepunitBasis n-te palindromische DreieckszahlBasis:
| nBasis | DreieckszahlBasis | ndezimal | Dreieckszahldezimal |
|---|---|---|---|
| 111111111111hex | 91A2B3C4D5EE5D4C3B2A19hex | 18764998447377dezimal | 176062583365039992818313753dezimal |
| 11111111111111hex | 91A2B3C4D5E6FF6E5D4C3B2A19hex | 4803839602528529dezimal | 11538437463410730145064930716185dezimal |
Algorithmus
Bildungsalgorithmus für die größte palindromische Dreieckszahl in einem Stellenwertsystem mit einer geradezahligen Basis > 2.
- Die n-te Dreieckszahl wird bestimmt durch eine Repunit zur ausgewählten Basis b mit b-2 Ziffern (Stellen).
- Die Anzahl der Ziffern der palindromischen Dreieckszahl ist (b-3)*2, die erste Hälfte der Palindromzahl hat somit b-3 Ziffern.
- Die erste Stelle der palindromischen Dreieckszahl erhält die Ziffer b/2+1.
- Die zweite Stelle der ersten Hälfte der Palindromzahl (sofern vorhanden) erhält die Ziffer 1.
- Die weiteren Stellen der ersten Hälfte der Palindromzahl (sofern vorhanden) erhalten die um 1 erhöhten Ziffern der vorvorherigen Stelle.
- Die zweite Hälfte der palindromischen Dreieckszahl wird dann durch Anhängen der gespiegelten Ziffernfolge gebildet.
Mehr zu Dreieckszahlen
Zu: Alle Dreieckszahlen > 3 sich zusammengesetzte Zahlen
- Bei allen (Dreieckszahlen > 6) - 1 handelt es sich ebenfalls um zusammengesetzte Zahlen.
Von Quadraten zu den Dreieckszahlen
Wird eine ungerade Zahl quadriert, dann 1 subtrahiert und der Differenzwert durch 8 dividiert, dann ergibt es immer eine Dreieckszahl .
Pascalsches Dreieck und Palindromzahlen
Im Pascalschen Dreieck können die Zeilen als Palindromzahlen angesehen werden, wobei die einzelnen Zahlen dann als Symbole für die Ziffern in einem b-adischen Zahlensystem stehen. Die Quersumme dieser Ziffern in einer Zeile ergeben bekanntlich Zweierpotenzen. (Siehe auch: Binomialkoeffizient)
Pythonprogramm zur Berechnung von Zeilen des Pascalschen Dreiecks. (Download: Portable Python 2.6.1)
Hier von Zeile 0 bis 50
#!Pascalsches Dreieck (Zeilen 0 bis 50 als Palindromzahlen)
b=126410606437752+1 #! Basis b muss hinreichend gross sein
#! mindestens gr?sste "Ziffer" + 1
for p in range (0,51):
c=(b+1)**p #! entspricht: c=(b+1)^p
print""
while c>0:
print c%b, #! entspricht: print c-c//b*b oder (print c mod b)
c=c//b #! entspricht: c=int(c/b) oder c=c\b
Repunits, Euler-Dreieck, Fakultäten
0
1 0
2 1 0
3 4 2 0
4 11 14 6 0
5 26 64 66 24 0
6 57 244 456 384 120 0
7 120 846 2556 3744 2640 720 0
8 247 2778 12762 28944 34560 20880 5040 0
- Zweitletzte Spalte von links oben nach rechts unten n! (Fakultät)
- Zweite Spalte von rechts oben nach links unten 2n-n-1 (Euler-Dreieck) oeis:A000295 und oeis:A125128
- Drittletzte Spalte von links oben nach rechts unten (n(n+1)/2+1)(n-1)!
- Viertletzte Spalte von links oben nach rechts unten oeis:A144335(n-2)!
Für die Zeilen gilt z.B.:
4 | 4+11=15 |15+25=40 |40+45=85 |... 11 |11+14=25 |25+20=45 |45+26=71 |... 14 |14+ 6=20 |20+ 6=26 |26+ 6=32 |... 6 | 6+ 0= 6 | 6+ 0= 6 | 6+ 0= 6 |... 0
Repunits zur Basis
4=11111 |15=11112 |40=11113 |85=11114 |...
Zweites Dreieck, Mersenne-Zahlen, Stirling-Zahlen, Fakultäten
0
1 0
3 1 0
7 6 2 0
15 25 20 6 0
31 90 130 90 24 0
63 301 700 840 504 120 0
127 966 3402 6300 6384 3360 720 0
255 3025 15540 41706 63504 55440 25920 5040 0
- Zweitletzte Spalte von links oben nach rechts unten n!
- Erste Spalte von rechts oben nach links unten 2n-1 (Mersenne-Zahlen)
- Zweite Spalte von rechts oben nach links unten 2n-n-1 (Stirling-Zahlen der zweiten Art) oeis:A000392
Vollkommene Zahlen
| Eine Zahl ist eine Vollkommene Zahl, wenn sie genauso groß ist wie die Summe ihrer positiven echten Teiler. Aus den Mersenne-Primzahlen lassen sich alle bekannten Vollkommenen Zahlen konstruieren. Die Verwandschaft läßt sich besonders leicht in der Binärdarstellung erkennen. | ||||||||
| binär | 110 | 11100 | 111110000 | 1111111000000 | 1111111111111000000000000 | 111111111111111110000000000000000 | 1111111111111111111000000000000000000 | … |
|---|---|---|---|---|---|---|---|---|
| potenz | (22-1)21 | (23-1)22 | (25-1)24 | (27-1)26 | (213-1)212 | (217-1)216 | (219-1)218 | … |
| dezimal | 6 | 28 | 496 | 8128 | 33550336 | 8589869056 | 137438691328 | … |
| Der binäre Darstellung einer Vollkomenen Zahl besteht aus der Mersenne-Primzahl, gefolgt von Ziffern „0“ mit einer um eine Stelle verringerten Anzahl. | ||||||||
Die Vollkommenen Zahlen gehören zu den „Freiwilligen Palindromzahlen“, denn in der Binärschreibweise kann die erforderliche Anzahl der Ziffern „0“ vor der Zahl ergänzt werden, ohne dass sich der Wert der Zahl verändert.
Beispiel: 11100 = 0011100 = Freiwillige Palindromzahl
Formel:
- alternativ
Vollkommene Zahlen (1. - 20.)
Die ersten 20 Vollkommenen Zahlen, die nach der oben angegebenen Formel mit den Mersenne-Primzahlen gebildet wurden, lauten:
- 6
- 28
- 496
- 8128
- 33550336
- 8589869056
- 137438691328
- 2305843008139952128
- 2658455991569831744654692615953842176
- 191561942608236107294793378084303638130997321548169216
- 13164036458569648337239753460458722910223472318386943117783728128
- 14474011154664524427946373126085988481573677491474835889066354349131199152128
- 23562723457267347065789548996709904988477547858392600710143027597506337283178622239730365539602600561360255566462503270175052892578043215543382498428777152427010394496918664028644534128033831439790236838624033171435922356643219703101720713163527487298747400647801939587165936401087419375649057918549492160555646976
- 141053783706712069063207958086063189881486743514715667838838675999954867742652380114104193329037690251561950568709829327164087724366370087116731268159313652487450652439805877296207297446723295166658228846926807786652870188920867879451478364569313922060370695064736073572378695176473055266826253284886383715072974324463835300053138429460296575143368065570759537328128
- 54162526284365847412654465374391316140856490539031695784603920818387206994158534859198999921056719921919057390080263646159280013827605439746262788903057303445505827028395139475207769044924431494861729435113126280837904930462740681717960465867348720992572190569465545299629919823431031092624244463547789635441481391719816441605586788092147886677321398756661624714551726964302217554281784254817319611951659855553573937788923405146222324506715979193757372820860878214322052227584537552897476256179395176624426314480313446935085203657584798247536021172880403783048602873621259313789994900336673941503747224966984028240806042108690077670395259231894666273615212775603535764707952250173858305171028603021234896647851363949928904973292145107505979911456221519899345764984291328
- 1089258355057829337698225273522048981957108454302608067318906618508470155298616996291940961858901379546182685531220055762780759342407499066046704182083087124626926378164410931450968826355205573671671624202686633360807123109470452668371537599662797484934359039779954213666598820299501366380164619080260403235229556730554163992303009752651350320619930563673695280153023049498468696618144072021372831425963701460505606378119245841386552600145384072983309717141950085498085709671387054868320477972299055273914798446936214147860706887052107312380067072602317009422809314774791894700769891009818743169303028154303290071199392984292940283852217800166629229157110264080599294016452483028528153331119523441423159614934140265550242360007858215936798489500727196347516386044241721984706558329364277995903102292034620628080752342422906401283027034649671445569324281946859622177566643375489715678451311792675935981010355562887971948569016060035334607879359770371846507659970601616998311983878150420763306289490886429900481786499537645379839365212725494441511932772182768149943659849007457246983861558265144823191367758350341527780770221556945275566504831636564856831502556078058133043400055653540413313266034639355202834006126905491569560542489551023207382276137352665717018261519604817417112576526410535323991500058749996247580834453782528
- 99497054337086473442435202604522816989643863571126408511774020575773849326355529178686629498151336416502516645641699516813140394897940636561646545947753232301453603583223268085613647233768081645727669037394385696522820301535888041815559513408036145123870584325525813950487109647770743827362571822870567643040184723115825645590386313377067112638149253171843914780065137373446222406322953569124771480101363180966448099882292453452395428270875732536311539266115116490704940164192417744919250000894727407937229829300578253427884494358459949535231819781361449649779252948099909821642207485514805768288115583409148969875790523961878753124972681179944234641016960011815788847436610192704551637034472552319820336532014561412028820492176940418377074274389149924303484945446105121267538061583299291707972378807395016030765440655601759109370564522647989156121804273012266011783451102230081380401951383582987149578229940818181514046314819313206321375973336785023565443101305633127610230549588655605951332351485641757542611227108073263889434409595976835137412187025349639504404061654653755349162680629290551644153382760681862294677414989047491922795707210920437811136712794483496437355980833463329592838140157803182055197821702739206310971006260383262542900044072533196137796552746439051760940430082375641150129817960183028081010978780902441733680977714813543438752546136375675139915776
- 33570832131986724437010877211080384841138028499879725454996241573482158450444042882048778809437690388449535774260849885573694759906173841157438424730130807047623655942236174850509108537827658590642325482494761473196579074656099918600764404702181660294469121778737965822199901663478093006075022359223201849985636144177185925402078185073015045097727084859464743635537781500284915880244886306461785982956072060013474955617851481680185988557136609224841817877083608951191123174885226416130683197710667392351007374503755403352531476227943590071651702697594241031955529898971218001214641774673134944471562560957179657881556419122102935450299751813340515170956167951095453649485576150660101689160658011770193274226308280507786835049549112576654510119670456745939890194205255175384484489909328967646988163155982471564998196261632751283127879509198074253193409580454562488664383465379885002735506153988851506645137759275553988219425439764732399824712438125054117523837438256744437055019441051006489972341609117978404563794992004873057518455748701444951238377139620494287982489529827233140637014837408856156199515457669607964052126908149265601786094447595560440059050091763547114092255371397425807867554352112542194784815494784276201170845949274674632985210421075531784918358926690395463649721452265405713484388043911634485432358638806645313826206591131266232422007835577345584225720310518698143376736219283021119287617896146885584860065048876315701088796219593640826311622273328035603309475642390804499460156797855361018246696101253922254567240908315385468240931846166962495983407607141601251889544407008815874744654769507268678051757746956891212485456261121386667407711139619071530923355823178662705374393035049022603882479742334799407130280148769298597743778193050348749740786928096033906295910199238181338557856978191860647256209708168229116156300978059197026855726877649767072684960463452763160384093838292277544911857859658328888332628525056
- 18201749040140430273835167914751015293362889506937596103357359437740048438463485836303232258902400875568993809975036246337556768238366233707757573415903278080066115951092522543145952013119010340408099881835975590975835499003463227280543140756802691525621894771543951403656868707748606069885095036335283528581813088651653833089052785834280723280067200484903706704970113521040604064538274154252165373175595605248628998615687866235395077520314640188634353318831397392517095413127961059169783805545093120277974213161792712750189234973622853507624924636687588461310469170436099238232492598937308477793932361698480685664770932715430491007662682405163044765107996164343261202355969912750334459238591875176292279879181327972920090211444842306766331109269166235125509668704478958734853068636529397153443016761158813447481567868262367893981171020212189792514086148090215189947704212407282687964267041783873543080261582448824858431838554183153705837057341487700727731550997896239330477471263230726484877117521254868468174015562068490713644719481693089433418532636835808942200716440819313366362403191355576523173825131875335647759016207232990842875902548737480801898289658229210850221695663421649611729577245208490877897945867171915873804061345544603919338281884397538634259920738193259330950837923823615411304543599290641330796754637229721314074245135865275394292301532835414540035740253567232435673868968242806554916467387945199026147468808031055150281915733287931898181708779241724409277593094799901224641825850183281480975988801751016901958988814849430087926938683408662084176896164178170688871544229415824450055526787148715365214142372692896788902761679810950828268208180845309986581369910322372338718437892376924042425319226250711104694125177110946650435829229609212441927473293781744486775943173110295432226780186422343937384580708855852269417012387614583884866613236875101300845603785945237925447338784922452682337026775686191693583794243538309813874806083439394116832472101884074936138517168612519077402832074575032255369216417037979614393919019507244388546924316787128440250098924928769352393698587810869831127888084696751795845351130410199628821737636610886633120714458623846784948362409208330416268144841565505869827619451490634144640754203543507421045031995754480556197763855213987476437990952173006055503017305481394836591954388794314558786433824434673257753459825605748638411145315395326160048592155490496363095590187403880545069860151237473584639382355987779291886392614452838326884468500853448420623482240841078202705004101172745586672975106848437133377536
- 40767271711094423266286789500920409509472451956754173657558947684464681715260993357605734441071512726995067528227747339481802307406017975918463751821848507118336173625166416441051751909733833921511752076653991689253045435925355114303300112240094312492366309429025181937703076074631694330891971804062290637324463063370007444165676699382865548574698013900725344417715580901794517787294713626725247616431165717354475083506329812661542345174259067891050196093969424325393268526237129649381671501429508518532700654319135658688537822432173525578067619513381189044904675194018182193349875318307576479629202619084300084497552929130566459016664436323063518973396208264181441158994259766077215199598273505770807393645474832736784296681037040447804670653738245607704296033370069548245058222346937754342008266115596746009270472531585662215058309416971412450120373149200391305139626391147758497714062124945414219545021663761325651848979096956363445054874071200187004098334242171313866643279783121709224161095222080608666106221075196556669546036212033916214620015754946773858930331944632744676736422424630471770419404321630175578272380575860947613876452571102541656491464344575071152521057073596731123384560986412117728286743021819378916115542964437048959026512685144124956065485652281953670546881779736097894174076453897164963235414848542178185638376039787558515854327876892100291586150169593481653250617283841617035992495539326209286081463451168016943400175227907739209129141984002670216279803245614932227988255785347373220924269748847852670574748163344676257876208108900678912830541369572996543783984620215364954353893838464888672671453393130927672103268849597298792373028395452767031129100333696063046099180328138782391367566104347713165495897021159454503241952055937183814515589264894586591501363147676413662843302502175075791426238440513015405476007476498747783201892106205584698383524005031036187539925202274453467202350823213372999023061199920256689198899908817944610695281886646630824678765305845231339408011870948795735488385897157930791657525540518959449984465130248721166519809265271872913736358591494923276213116461018047328995621925367809697847697726183327599265650527446129800629718921404375627930737500435684546352140119118622625161732119556975036023320412126344181833754571377867747583783758174317957011000027824913530257131124993626863404596480086028834672069335493603141485087204213357254720762673897857837928958409382883536405344396217119883289266162616394049286804626796372654015917535645430198053751867174961912991147525380624081763689015391680510756697550659469557112900507657356152843089480485079285160832736274980123243426924630558985552020642912534528
Länge der Sehne (Kreis) mit dem Pythagoras
Die Länge der Sehne in einem Kreis läßt sich berechnen, wenn der Radius des Kreises und der Abstand der Sehne vom Mittelpunkt des Kreises bekannt ist. Der Abstand a und die halbe Sehne x bilden immer die Katheten eines rechtwinkligen Dreiecks. Der Radius r entspricht immer der Hypotenuse. Mit dem Satz des Pythagoras läßt sich leicht die Länge der Sehne s ermitteln.
Pythagoras:
Formel nach x umgestellt:
Sehne gleich 2x:
Annäherung an π mit dem Pythagoras
Es gibt viele Brechnungsmethoden für die Kreiszahl π. Eine läßt sich über die Berechnung von Kreissehnen verwirklichen. Wie oben gezeigt, läßt sich die halbe Länge einer Sehne mit dem Pythagoras direkt berechnen. Werden viele halbe Sehnen zwischen Mittelpunkt und Radius berechnet, dann nähert sich der Mittelwert π/4 an, wenn der Radius 1 gewählt wird.
Besondere primitive pythagoreische Tripel
Siehe auch: Pythagoreisches Tripel
- Für jede ungerade Zahl >1 gilt, wenn sie als „a“ (Gegenkathete) eines rechtwinkligen Dreiecks genommen wird, dass sich immer ein pythagoreisches Zahlentripel bilden läßt.
- Die Ankathete „b“ ist zu bilden mit (a^2-1)/2
- Die Hypotenuse „c“ ist zu bilden mit (a^2+1)/2
- Es gilt also: (natürlich) a^2+b^2=c^2 und b+c=a^2 und b=c-1 und c ist ungerade und b gerade
Nach diesen Regeln erhält man folgende primitive pythagoreische Tripel.
| a | b | c |
|---|---|---|
| 3 | 4 | 5 |
| 5 | 12 | 13 |
| 7 | 24 | 25 |
| 9 | 40 | 41 |
| 11 | 60 | 61 |
| 13 | 84 | 85 |
| ... | ... | ... |
Tripel mit zwei Primzahlen
Pythagoreische Tripel mit zwei Primzahlen haben immer die oben beschriebene Form. Wobei die Seiten a und c die Primzahlen sind.
Die Tabelle dieser Tripel beginnt dann wie folgt:
| aprime | b | cprime |
|---|---|---|
| 3 | 4 | 5 |
| 5 | 12 | 13 |
| 11 | 60 | 61 |
| 19 | 180 | 181 |
| 29 | 420 | 421 |
| 59 | 1740 | 1741 |
| ... | ... | ... |
Primzahl = a+b
Wenn zusätzlich die Bedingung gestellt wird, dass a+b ebenfalls eine Primzahl sein soll, dann sieht die Tabelle so aus:
| aprime | b | cprime | a+b(prime) |
|---|---|---|---|
| 3 | 4 | 5 | 7 |
| 5 | 12 | 13 | 17 |
| 11 | 60 | 61 | 71 |
| 19 | 180 | 181 | 199 |
| 29 | 420 | 421 | 449 |
| 71 | 2520 | 2521 | 2591 |
| ... | ... | ... | ... |
Primzahl = a+b+ größter Primfaktor (b)
Wenn die Summe der größten Primfaktoren der Seiten (a+c+b)>prime eine Primzahl ist, dann ergibt sich folgende Tabelle:
| aprime | b | cprime | b>prime factor | a+c+b>prime factor(prime) |
|---|---|---|---|---|
| 29 | 420 | 421 | 7 | 457 |
| 199 | 19800 | 19801 | 11 | 20011 |
| 1091 | 595140 | 595141 | 109 | 596341 |
| 2711 | 3674760 | 3674761 | 271 | 3677743 |
| 3491 | 6093540 | 6093541 | 349 | 6097381 |
| 4691 | 11002740 | 11002741 | 67 | 11007499 |
| ... | ... | ... | ... | ... |
Auffällig ist hier, dass viele größte Primfaktoren von b in einem besonderen Verhältnis zu a stehen. Es gibt häufig die Konstellation (a-1)/10 = b>prime factor
Perfekte und Fast Perfekte Primzahlen (rechtsstutzbare Primzahlen)
Seite hierzu: Truncatable prime
Weitere Seiten:Madbros/Perfekte Primzahl und Thogo/Fast Perfekte Primzahl
- Primzahlen sollen dann Perfekte Primzahlen heißen, wenn sie durch das wiederholte Anhängen einer Ziffer an eine Primzahl entstanden sind und das Anhängen jeder weiteren beliebigen Ziffer keine Primzahl mehr ergibt.
- Primzahlen sollen dann Fast Perfekte Primzahlen heißen, wenn sie eine einstellige Primzahl sind oder durch das wiederholte Anhängen einer Ziffer an eine Primzahl entstanden sind. Die Perfekten Primzahlen sind somit eine Teilmenge der Fast Perfekten Primzahlen.
Die Fast Perfekten Primzahlen und die Perfekten Primzahlen sind abhängug vom verwendeten Stellenwertsystem. So gibt es im Binärsystem keine Fast Perfekten Primzahlen (und damit auch keine Perfekten Primzahlen) weil weder 0 noch 1 Primzahlen sind.
Basis 3 mit 4 Fast Perfekten Primzahlen
- (Siehe hierzu auch: A129669)
(Perfekte Primzahlen sind fett gedruckt)
| n | Basis 3 | Dezimal |
|---|---|---|
| 1. | 2 | 2 |
| 2. | 21 | 7 |
| 3. | 212 | 23 |
| 4. | 2122 | 71 |
Es gibt eine Perfekte Primzahl zur Basis 3
| n | Basis 3 | Dezimal |
|---|---|---|
| 1. | 2122 | 71 |
Basis 4 mit 7 Fast Perfekten Primzahlen
- (Siehe hierzu auch: A129670)
(Perfekte Primzahlen sind fett gedruckt)
| n | Basis 4 | Dezimal |
|---|---|---|
| 1. | 2 | 2 |
| 2. | 3 | 3 |
| 3. | 23 | 11 |
| 4. | 31 | 13 |
| 5. | 233 | 47 |
| 6. | 311 | 53 |
| 7. | 2333 | 191 |
Es gibt 2 Perfekte Primzahlen zur Basis 4
| n | Basis 4 | Dezimal |
|---|---|---|
| 1. | 311 | 53 |
| 2. | 2333 | 191 |
Basis 5 mit 14 Fast Perfekten Primzahlen
(Perfekte Primzahlen sind fett gedruckt)
| n | Basis 5 | Dezimal |
|---|---|---|
| 1. | 2 | 2 |
| 2. | 3 | 3 |
| 3. | 21 | 11 |
| 4. | 23 | 13 |
| 5. | 32 | 17 |
| 6. | 34 | 19 |
| 7. | 214 | 59 |
| 8. | 232 | 67 |
| 9. | 324 | 89 |
| 10. | 342 | 97 |
| 11. | 2322 | 337 |
| 12. | 3244 | 449 |
| 13. | 3422 | 487 |
| 14. | 34222 | 2437 |
Es gibt 4 Perfekte Primzahlen zur Basis 5
| n | Basis 5 | Dezimal |
|---|---|---|
| 1. | 214 | 59 |
| 2. | 2322 | 337 |
| 3. | 3244 | 449 |
| 4. | 34222 | 2437 |
Basis 6 mit 36 Fast Perfekten Primzahlen
- (Siehe hierzu auch: A129672)
(Perfekte Primzahlen sind fett gedruckt)
| n | Basis 6 | Dezimal |
|---|---|---|
| 1. | 2 | 2 |
| 2. | 3 | 3 |
| 3. | 5 | 5 |
| 4. | 21 | 13 |
| 5. | 25 | 17 |
| 6. | 31 | 19 |
| 7. | 35 | 23 |
| 8. | 51 | 31 |
| 9. | 211 | 79 |
| 10. | 215 | 83 |
| 11. | 251 | 103 |
| 12. | 255 | 107 |
| 13. | 351 | 139 |
| 14. | 515 | 191 |
| 15. | 2115 | 479 |
| 16. | 2151 | 499 |
| 17. | 2155 | 503 |
| 18. | 2511 | 619 |
| 19. | 2551 | 643 |
| 20. | 2555 | 647 |
| 21. | 3515 | 839 |
| 22. | 5155 | 1151 |
| 23. | 21155 | 2879 |
| 24. | 21515 | 2999 |
| 25. | 21551 | 3019 |
| 26. | 21555 | 3023 |
| 27. | 25115 | 3719 |
| 28. | 25515 | 3863 |
| 29. | 35155 | 5039 |
| 30. | 51551 | 6907 |
| 31. | 51555 | 6911 |
| 32. | 215515 | 18119 |
| 33. | 215555 | 18143 |
| 34. | 515511 | 41443 |
| 35. | 515551 | 41467 |
| 36. | 2155555 | 108863 |
Es gibt 11 Perfekte Primzahlen zur Basis 6
| n | Basis 6 | Dezimal |
|---|---|---|
| 1. | 31 | 19 |
| 2. | 2555 | 647 |
| 3. | 21155 | 2879 |
| 4. | 21515 | 2999 |
| 5. | 25115 | 3719 |
| 6. | 25515 | 3863 |
| 7. | 35155 | 5039 |
| 8. | 215515 | 18119 |
| 9. | 515511 | 41443 |
| 10. | 515551 | 41467 |
| 11. | 2155555 | 108863 |
Basis 7 mit 19 Fast Perfekten Primzahlen
- (Siehe hierzu auch: A129673)
(Perfekte Primzahlen sind fett gedruckt)
| n | Basis 7 | Dezimal |
|---|---|---|
| 1. | 2 | 2 |
| 2. | 3 | 3 |
| 3. | 5 | 5 |
| 4. | 23 | 17 |
| 5. | 25 | 19 |
| 6. | 32 | 23 |
| 7. | 52 | 37 |
| 8. | 56 | 41 |
| 9. | 254 | 137 |
| 10. | 256 | 139 |
| 11. | 322 | 163 |
| 12. | 326 | 167 |
| 13. | 524 | 263 |
| 14. | 566 | 293 |
| 15. | 2564 | 977 |
| 16. | 3262 | 1171 |
| 17. | 5246 | 1847 |
| 18. | 5662 | 2053 |
| 19. | 25642 | 6841 |
Es gibt 7 Perfekte Primzahlen zur Basis 7
| n | Basis 7 | Dezimal |
|---|---|---|
| 1. | 23 | 17 |
| 2. | 254 | 137 |
| 3. | 322 | 163 |
| 4. | 3262 | 1171 |
| 5. | 5246 | 1847 |
| 6. | 5662 | 2053 |
| 7. | 25642 | 6841 |
Basis 8 mit 68 Fast Perfekten Primzahlen
- (Siehe hierzu auch: A129692)
(Perfekte Primzahlen sind fett gedruckt)
| n | Basis 8 | Dezimal |
|---|---|---|
| 1. | 2 | 2 |
| 2. | 3 | 3 |
| 3. | 5 | 5 |
| 4. | 7 | 7 |
| 5. | 21 | 17 |
| 6. | 23 | 19 |
| 7. | 27 | 23 |
| 8. | 35 | 29 |
| 9. | 37 | 31 |
| 10. | 51 | 41 |
| 11. | 53 | 43 |
| 12. | 57 | 47 |
| 13. | 73 | 59 |
| 14. | 75 | 61 |
| 15. | 211 | 137 |
| 16. | 213 | 139 |
| 17. | 235 | 157 |
| 18. | 277 | 191 |
| 19. | 351 | 233 |
| 20. | 357 | 239 |
| 21. | 373 | 251 |
| 22. | 513 | 331 |
| 23. | 533 | 347 |
| 24. | 535 | 349 |
| 25. | 573 | 379 |
| 26. | 577 | 383 |
| 27. | 737 | 479 |
| 28. | 753 | 491 |
| 29. | 2111 | 1097 |
| 30. | 2117 | 1103 |
| 31. | 2135 | 1117 |
| 32. | 2353 | 1259 |
| 33. | 2773 | 1531 |
| 34. | 3513 | 1867 |
| 35. | 3517 | 1871 |
| 36. | 3571 | 1913 |
| 37. | 3733 | 2011 |
| 38. | 5331 | 2777 |
| 39. | 5355 | 2797 |
| 40. | 5735 | 3037 |
| 41. | 5773 | 3067 |
| 42. | 7371 | 3833 |
| 43. | 7531 | 3929 |
| 44. | 7533 | 3931 |
| 45. | 21113 | 8779 |
| 46. | 21117 | 8783 |
| 47. | 21177 | 8831 |
| 48. | 21355 | 8941 |
| 49. | 23537 | 10079 |
| 50. | 27733 | 12251 |
| 51. | 27735 | 12253 |
| 52. | 35133 | 14939 |
| 53. | 35171 | 14969 |
| 54. | 35713 | 15307 |
| 55. | 37333 | 16091 |
| 56. | 53555 | 22381 |
| 57. | 73717 | 30671 |
| 58. | 211135 | 70237 |
| 59. | 211177 | 70271 |
| 60. | 277331 | 98009 |
| 61. | 277333 | 98011 |
| 62. | 351331 | 119513 |
| 63. | 351717 | 119759 |
| 64. | 535553 | 179051 |
| 65. | 2111771 | 562169 |
| 66. | 3513313 | 956107 |
| 67. | 5355533 | 1432411 |
| 68. | 21117717 | 4497359 |
Es gibt 20 Perfekte Primzahlen zur Basis 8
| n | Basis 8 | Dezimal |
|---|---|---|
| 1. | 513 | 331 |
| 2. | 5331 | 2777 |
| 3. | 5735 | 3037 |
| 4. | 5773 | 3067 |
| 5. | 7531 | 3929 |
| 6. | 7533 | 3931 |
| 7. | 21177 | 8831 |
| 8. | 21355 | 8941 |
| 9. | 23537 | 10079 |
| 10. | 27735 | 12253 |
| 11. | 35713 | 15307 |
| 12. | 37333 | 16091 |
| 13. | 73717 | 30671 |
| 14. | 211135 | 70237 |
| 15. | 277331 | 98009 |
| 16. | 277333 | 98011 |
| 17. | 351717 | 119759 |
| 18. | 3513313 | 956107 |
| 19. | 5355533 | 1432411 |
| 20. | 21117717 | 4497359 |
Basis 9 mit 68 Fast Perfekten Primzahlen
- (Siehe hierzu auch: A129693)
(Perfekte Primzahlen sind fett gedruckt)
| n | Basis 9 | Dezimal |
|---|---|---|
| 1. | 2 | 2 |
| 2. | 3 | 3 |
| 3. | 5 | 5 |
| 4. | 7 | 7 |
| 5. | 21 | 19 |
| 6. | 25 | 23 |
| 7. | 32 | 29 |
| 8. | 34 | 31 |
| 9. | 52 | 47 |
| 10. | 58 | 53 |
| 11. | 74 | 67 |
| 12. | 78 | 71 |
| 13. | 212 | 173 |
| 14. | 218 | 179 |
| 15. | 254 | 211 |
| 16. | 322 | 263 |
| 17. | 328 | 269 |
| 18. | 342 | 281 |
| 19. | 344 | 283 |
| 20. | 528 | 431 |
| 21. | 582 | 479 |
| 22. | 744 | 607 |
| 23. | 782 | 641 |
| 24. | 784 | 643 |
| 25. | 788 | 647 |
| 26. | 2122 | 1559 |
| 27. | 2182 | 1613 |
| 28. | 2188 | 1619 |
| 29. | 2542 | 1901 |
| 30. | 2548 | 1907 |
| 31. | 3224 | 2371 |
| 32. | 3282 | 2423 |
| 33. | 3422 | 2531 |
| 34. | 3442 | 2549 |
| 35. | 3444 | 2551 |
| 36. | 5282 | 3881 |
| 37. | 7448 | 5471 |
| 38. | 7844 | 5791 |
| 39. | 7884 | 5827 |
| 40. | 21222 | 14033 |
| 41. | 21822 | 14519 |
| 42. | 25428 | 17117 |
| 43. | 25484 | 17167 |
| 44. | 32242 | 21341 |
| 45. | 32248 | 21347 |
| 46. | 34224 | 22783 |
| 47. | 34228 | 22787 |
| 48. | 34422 | 22943 |
| 49. | 34442 | 22961 |
| 50. | 34444 | 22963 |
| 51. | 78442 | 52121 |
| 52. | 78448 | 52127 |
| 53. | 254284 | 154057 |
| 54. | 254288 | 154061 |
| 55. | 344222 | 206489 |
| 56. | 344422 | 206651 |
| 57. | 2542882 | 1386551 |
| 58. | 2542888 | 1386557 |
| 59. | 3442222 | 1858403 |
| 60. | 3444224 | 1859863 |
| 61. | 25428888 | 12479021 |
| 62. | 34422222 | 16725629 |
| 63. | 34442242 | 16738769 |
| 64. | 254288882 | 112311191 |
| 65. | 344422422 | 150648923 |
| 66. | 2542888824 | 1010800723 |
| 67. | 2542888828 | 1010800727 |
| 68. | 3444224222 | 1355840309 |
Es gibt 23 Perfekte Primzahlen zur Basis 9
| n | Basis 9 | Dezimal |
|---|---|---|
| 1. | 582 | 479 |
| 2. | 782 | 641 |
| 3. | 2188 | 1619 |
| 4. | 3282 | 2423 |
| 5. | 5282 | 3881 |
| 6. | 7448 | 5471 |
| 7. | 7884 | 5827 |
| 8. | 21222 | 14033 |
| 9. | 21822 | 14519 |
| 10. | 25484 | 17167 |
| 11. | 32242 | 21341 |
| 12. | 32248 | 21347 |
| 13. | 34224 | 22783 |
| 14. | 34228 | 22787 |
| 15. | 34444 | 22963 |
| 16. | 78442 | 52121 |
| 17. | 78448 | 52127 |
| 18. | 254284 | 154057 |
| 19. | 2542882 | 1386551 |
| 20. | 34422222 | 16725629 |
| 21. | 2542888824 | 1010800723 |
| 22. | 2542888828 | 1010800727 |
| 23. | 3444224222 | 1355840309 |
Basis 10 mit 83 Fast Perfekten Primzahlen
- (Siehe hierzu auch: A024770)
(Perfekte Primzahlen sind fett gedruckt)
| n | Basis 10 | Dezimal |
|---|---|---|
| 1. | 2 | 2 |
| 2. | 3 | 3 |
| 3. | 5 | 5 |
| 4. | 7 | 7 |
| 5. | 23 | 23 |
| 6. | 29 | 29 |
| 7. | 31 | 31 |
| 8. | 37 | 37 |
| 9. | 53 | 53 |
| 10. | 59 | 59 |
| 11. | 71 | 71 |
| 12. | 73 | 73 |
| 13. | 79 | 79 |
| 14. | 233 | 233 |
| 15. | 239 | 239 |
| 16. | 293 | 293 |
| 17. | 311 | 311 |
| 18. | 313 | 313 |
| 19. | 317 | 317 |
| 20. | 373 | 373 |
| 21. | 379 | 379 |
| 22. | 593 | 593 |
| 23. | 599 | 599 |
| 24. | 719 | 719 |
| 25. | 733 | 733 |
| 26. | 739 | 739 |
| 27. | 797 | 797 |
| 28. | 2333 | 2333 |
| 29. | 2339 | 2339 |
| 30. | 2393 | 2393 |
| 31. | 2399 | 2399 |
| 32. | 2939 | 2939 |
| 33. | 3119 | 3119 |
| 34. | 3137 | 3137 |
| 35. | 3733 | 3733 |
| 36. | 3739 | 3739 |
| 37. | 3793 | 3793 |
| 38. | 3797 | 3797 |
| 39. | 5939 | 5939 |
| 40. | 7193 | 7193 |
| 41. | 7331 | 7331 |
| 42. | 7333 | 7333 |
| 43. | 7393 | 7393 |
| 44. | 23333 | 23333 |
| 45. | 23339 | 23339 |
| 46. | 23399 | 23399 |
| 47. | 23993 | 23993 |
| 48. | 29399 | 29399 |
| 49. | 31193 | 31193 |
| 50. | 31379 | 31379 |
| 51. | 37337 | 37337 |
| 52. | 37339 | 37339 |
| 53. | 37397 | 37397 |
| 54. | 59393 | 59393 |
| 55. | 59399 | 59399 |
| 56. | 71933 | 71933 |
| 57. | 73331 | 73331 |
| 58. | 73939 | 73939 |
| 59. | 233993 | 233993 |
| 60. | 239933 | 239933 |
| 61. | 293999 | 293999 |
| 62. | 373379 | 373379 |
| 63. | 373393 | 373393 |
| 64. | 593933 | 593933 |
| 65. | 593993 | 593993 |
| 66. | 719333 | 719333 |
| 67. | 739391 | 739391 |
| 68. | 739393 | 739393 |
| 69. | 739397 | 739397 |
| 70. | 739399 | 739399 |
| 71. | 2339933 | 2339933 |
| 72. | 2399333 | 2399333 |
| 73. | 2939999 | 2939999 |
| 74. | 3733799 | 3733799 |
| 75. | 5939333 | 5939333 |
| 76. | 7393913 | 7393913 |
| 77. | 7393931 | 7393931 |
| 78. | 7393933 | 7393933 |
| 79. | 23399339 | 23399339 |
| 80. | 29399999 | 29399999 |
| 81. | 37337999 | 37337999 |
| 82. | 59393339 | 59393339 |
| 83. | 73939133 | 73939133 |
Es gibt 27 Perfekte Primzahlen zur Basis 10
| n | Basis 10 | Dezimal |
|---|---|---|
| 1. | 53 | 53 |
| 2. | 317 | 317 |
| 3. | 599 | 599 |
| 4. | 797 | 797 |
| 5. | 2393 | 2393 |
| 6. | 3793 | 3793 |
| 7. | 3797 | 3797 |
| 8. | 7331 | 7331 |
| 9. | 23333 | 23333 |
| 10. | 23339 | 23339 |
| 11. | 31193 | 31193 |
| 12. | 31379 | 31379 |
| 13. | 37397 | 37397 |
| 14. | 73331 | 73331 |
| 15. | 373393 | 373393 |
| 16. | 593993 | 593993 |
| 17. | 719333 | 719333 |
| 18. | 739397 | 739397 |
| 19. | 739399 | 739399 |
| 20. | 2399333 | 2399333 |
| 21. | 7393931 | 7393931 |
| 22. | 7393933 | 7393933 |
| 23. | 23399339 | 23399339 |
| 24. | 29399999 | 29399999 |
| 25. | 37337999 | 37337999 |
| 26. | 59393339 | 59393339 |
| 27. | 73939133 | 73939133 |
Basis 11 mit 89 Fast Perfekten Primzahlen
(Perfekte Primzahlen sind fett gedruckt)
| n | Basis 11 | Dezimal |
|---|---|---|
| 1. | 2 | 2 |
| 2. | 3 | 3 |
| 3. | 5 | 5 |
| 4. | 7 | 7 |
| 5. | 21 | 23 |
| 6. | 27 | 29 |
| 7. | 29 | 31 |
| 8. | 34 | 37 |
| 9. | 38 | 41 |
| 10. | 3A | 43 |
| 11. | 54 | 59 |
| 12. | 56 | 61 |
| 13. | 72 | 79 |
| 14. | 76 | 83 |
| 15. | 214 | 257 |
| 16. | 21A | 263 |
| 17. | 296 | 347 |
| 18. | 298 | 349 |
| 19. | 342 | 409 |
| 20. | 386 | 457 |
| 21. | 38A | 461 |
| 22. | 3A6 | 479 |
| 23. | 544 | 653 |
| 24. | 54A | 659 |
| 25. | 562 | 673 |
| 26. | 566 | 677 |
| 27. | 728 | 877 |
| 28. | 766 | 919 |
| 29. | 2146 | 2833 |
| 30. | 214A | 2837 |
| 31. | 21A4 | 2897 |
| 32. | 21AA | 2903 |
| 33. | 2964 | 3821 |
| 34. | 2966 | 3823 |
| 35. | 2988 | 3847 |
| 36. | 3428 | 4507 |
| 37. | 38A6 | 5077 |
| 38. | 38AA | 5081 |
| 39. | 3A64 | 5273 |
| 40. | 3A6A | 5279 |
| 41. | 5444 | 7187 |
| 42. | 544A | 7193 |
| 43. | 54A4 | 7253 |
| 44. | 5628 | 7411 |
| 45. | 5664 | 7451 |
| 46. | 566A | 7457 |
| 47. | 7282 | 9649 |
| 48. | 7662 | 10111 |
| 49. | 21A46 | 31873 |
| 50. | 29668 | 42061 |
| 51. | 29886 | 42323 |
| 52. | 38A62 | 55849 |
| 53. | 38AA6 | 55897 |
| 54. | 38AAA | 55901 |
| 55. | 3A64A | 58013 |
| 56. | 3A6A4 | 58073 |
| 57. | 54446 | 79063 |
| 58. | 544AA | 79133 |
| 59. | 56286 | 81527 |
| 60. | 56646 | 81967 |
| 61. | 5664A | 81971 |
| 62. | 566A4 | 82031 |
| 63. | 566AA | 82037 |
| 64. | 76626 | 111227 |
| 65. | 76628 | 111229 |
| 66. | 296682 | 462673 |
| 67. | 296686 | 462677 |
| 68. | 38AAA6 | 614917 |
| 69. | 3A64A4 | 638147 |
| 70. | 562866 | 896803 |
| 71. | 566466 | 901643 |
| 72. | 5664A6 | 901687 |
| 73. | 566A46 | 902347 |
| 74. | 566A4A | 902351 |
| 75. | 566AA6 | 902413 |
| 76. | 766288 | 1223527 |
| 77. | 2966828 | 5089411 |
| 78. | 2966864 | 5089451 |
| 79. | 5628666 | 9864839 |
| 80. | 5664A66 | 9918563 |
| 81. | 566A466 | 9925823 |
| 82. | 7662882 | 13458799 |
| 83. | 29668286 | 55983527 |
| 84. | 2966864A | 55983971 |
| 85. | 56286664 | 108513233 |
| 86. | 566A4664 | 109184057 |
| 87. | 76628828 | 148046797 |
| 88. | 29668286A | 615818807 |
| 89. | 29668286AA | 6774006887 |
Es gibt 28 Perfekte Primzahlen zur Basis 11
| n | Basis 11 | Dezimal |
|---|---|---|
| 1. | 27 | 29 |
| 2. | 386 | 457 |
| 3. | 2146 | 2833 |
| 4. | 214A | 2837 |
| 5. | 21AA | 2903 |
| 6. | 2964 | 3821 |
| 7. | 3428 | 4507 |
| 8. | 54A4 | 7253 |
| 9. | 7282 | 9649 |
| 10. | 21A46 | 31873 |
| 11. | 29886 | 42323 |
| 12. | 38A62 | 55849 |
| 13. | 38AA6 | 55897 |
| 14. | 3A6A4 | 58073 |
| 15. | 54446 | 79063 |
| 16. | 544AA | 79133 |
| 17. | 76626 | 111227 |
| 18. | 38AAA6 | 614917 |
| 19. | 3A64A4 | 638147 |
| 20. | 566466 | 901643 |
| 21. | 566A4A | 902351 |
| 22. | 566AA6 | 902413 |
| 23. | 5664A66 | 9918563 |
| 24. | 2966864A | 55983971 |
| 25. | 56286664 | 108513233 |
| 26. | 566A4664 | 109184057 |
| 27. | 76628828 | 148046797 |
| 28. | 29668286AA | 6774006887 |
Basis 12 mit 179 Fast Perfekten Primzahlen
(Perfekte Primzahlen sind fett gedruckt)
| n | Basis 12 | Dezimal |
|---|---|---|
| 1. | 2 | 2 |
| 2. | 3 | 3 |
| 3. | 5 | 5 |
| 4. | 7 | 7 |
| 5. | B | 11 |
| 6. | 25 | 29 |
| 7. | 27 | 31 |
| 8. | 31 | 37 |
| 9. | 35 | 41 |
| 10. | 37 | 43 |
| 11. | 3B | 47 |
| 12. | 51 | 61 |
| 13. | 57 | 67 |
| 14. | 5B | 71 |
| 15. | 75 | 89 |
| 16. | B5 | 137 |
| 17. | B7 | 139 |
| 18. | 251 | 349 |
| 19. | 255 | 353 |
| 20. | 25B | 359 |
| 21. | 271 | 373 |
| 22. | 277 | 379 |
| 23. | 27B | 383 |
| 24. | 315 | 449 |
| 25. | 357 | 499 |
| 26. | 35B | 503 |
| 27. | 375 | 521 |
| 28. | 377 | 523 |
| 29. | 3B5 | 569 |
| 30. | 3B7 | 571 |
| 31. | 511 | 733 |
| 32. | 517 | 739 |
| 33. | 51B | 743 |
| 34. | 575 | 809 |
| 35. | 577 | 811 |
| 36. | 5B1 | 853 |
| 37. | 5B5 | 857 |
| 38. | 5B7 | 859 |
| 39. | 5BB | 863 |
| 40. | 751 | 1069 |
| 41. | B71 | 1669 |
| 42. | 2555 | 4241 |
| 43. | 2557 | 4243 |
| 44. | 2715 | 4481 |
| 45. | 2717 | 4483 |
| 46. | 2771 | 4549 |
| 47. | 27B1 | 4597 |
| 48. | 27B7 | 4603 |
| 49. | 3155 | 5393 |
| 50. | 315B | 5399 |
| 51. | 35B1 | 6037 |
| 52. | 35B7 | 6043 |
| 53. | 35BB | 6047 |
| 54. | 3755 | 6257 |
| 55. | 375B | 6263 |
| 56. | 3771 | 6277 |
| 57. | 377B | 6287 |
| 58. | 3B51 | 6829 |
| 59. | 3B55 | 6833 |
| 60. | 3B75 | 6857 |
| 61. | 3B7B | 6863 |
| 62. | 5117 | 8803 |
| 63. | 511B | 8807 |
| 64. | 51B7 | 8923 |
| 65. | 575B | 9719 |
| 66. | 5771 | 9733 |
| 67. | 5777 | 9739 |
| 68. | 577B | 9743 |
| 69. | 5B17 | 10243 |
| 70. | 5B1B | 10247 |
| 71. | 5B55 | 10289 |
| 72. | 5B75 | 10313 |
| 73. | 5BB1 | 10357 |
| 74. | 7511 | 12829 |
| 75. | B711 | 20029 |
| 76. | 25551 | 50893 |
| 77. | 25577 | 50923 |
| 78. | 27151 | 53773 |
| 79. | 27155 | 53777 |
| 80. | 2715B | 53783 |
| 81. | 27B17 | 55171 |
| 82. | 27B77 | 55243 |
| 83. | 31551 | 64717 |
| 84. | 315B5 | 64793 |
| 85. | 375B5 | 75161 |
| 86. | 375BB | 75167 |
| 87. | 37715 | 75329 |
| 88. | 3B515 | 81953 |
| 89. | 3B557 | 82003 |
| 90. | 3B55B | 82007 |
| 91. | 3B7B5 | 82361 |
| 92. | 511B7 | 105691 |
| 93. | 51B71 | 107077 |
| 94. | 575BB | 116639 |
| 95. | 57711 | 116797 |
| 96. | 57717 | 116803 |
| 97. | 577B7 | 116923 |
| 98. | 577BB | 116927 |
| 99. | 5B175 | 122921 |
| 100. | 5B1B7 | 122971 |
| 101. | 5B55B | 123479 |
| 102. | 5B751 | 123757 |
| 103. | 5BB17 | 124291 |
| 104. | 75111 | 153949 |
| 105. | 75115 | 153953 |
| 106. | B7111 | 240349 |
| 107. | B7115 | 240353 |
| 108. | 255515 | 610721 |
| 109. | 255775 | 611081 |
| 110. | 271555 | 645329 |
| 111. | 2715B1 | 645397 |
| 112. | 27B177 | 662059 |
| 113. | 27B17B | 662063 |
| 114. | 27B771 | 662917 |
| 115. | 375B55 | 901937 |
| 116. | 375BB5 | 902009 |
| 117. | 377151 | 903949 |
| 118. | 3B5155 | 983441 |
| 119. | 3B5157 | 983443 |
| 120. | 3B515B | 983447 |
| 121. | 3B5571 | 984037 |
| 122. | 3B557B | 984047 |
| 123. | 3B55B7 | 984091 |
| 124. | 3B7B5B | 988343 |
| 125. | 511B77 | 1268299 |
| 126. | 51B717 | 1284931 |
| 127. | 575BBB | 1399679 |
| 128. | 577117 | 1401571 |
| 129. | 577175 | 1401641 |
| 130. | 577B75 | 1403081 |
| 131. | 5B55B1 | 1481749 |
| 132. | 5B55BB | 1481759 |
| 133. | 5BB171 | 1491493 |
| 134. | 751115 | 1847393 |
| 135. | B71157 | 2884243 |
| 136. | 2715551 | 7743949 |
| 137. | 27B7715 | 7955009 |
| 138. | 27B7717 | 7955011 |
| 139. | 375B555 | 10823249 |
| 140. | 375B557 | 10823251 |
| 141. | 375BB5B | 10824119 |
| 142. | 3771515 | 10847393 |
| 143. | 3B5155B | 11801303 |
| 144. | 3B5157B | 11801327 |
| 145. | 3B55715 | 11808449 |
| 146. | 3B557B5 | 11808569 |
| 147. | 3B557B7 | 11808571 |
| 148. | 3B55B71 | 11809093 |
| 149. | 3B55B77 | 11809099 |
| 150. | 3B55B7B | 11809103 |
| 151. | 511B775 | 15219593 |
| 152. | 5771171 | 16818853 |
| 153. | 5771755 | 16819697 |
| 154. | 5B55B1B | 17780999 |
| 155. | 5B55BB1 | 17781109 |
| 156. | 5BB1711 | 17897917 |
| 157. | 7511151 | 22168717 |
| 158. | 7511157 | 22168723 |
| 159. | 27B77151 | 95460109 |
| 160. | 27B7715B | 95460119 |
| 161. | 27B77175 | 95460137 |
| 162. | 375BB5B5 | 129889433 |
| 163. | 3B5155BB | 141615647 |
| 164. | 3B5157B7 | 141615931 |
| 165. | 3B557151 | 141701389 |
| 166. | 3B557B75 | 141702857 |
| 167. | 3B55B775 | 141709193 |
| 168. | 3B55B7B5 | 141709241 |
| 169. | 3B55B7BB | 141709247 |
| 170. | 511B7755 | 182635121 |
| 171. | 5B55B1B5 | 213371993 |
| 172. | 27B771511 | 1145521309 |
| 173. | 27B771755 | 1145521649 |
| 174. | 375BB5B51 | 1558673197 |
| 175. | 375BB5B55 | 1558673201 |
| 176. | 3B5571515 | 1700416673 |
| 177. | 3B55B7755 | 1700510321 |
| 178. | 3B55B7B57 | 1700510899 |
| 179. | 375BB5B515 | 18704078369 |
Es gibt 61 Perfekte Primzahlen zur Basis 12
| n | Basis 12 | Dezimal |
|---|---|---|
| 1. | B5 | 137 |
| 2. | 251 | 349 |
| 3. | 25B | 359 |
| 4. | 357 | 499 |
| 5. | 517 | 739 |
| 6. | 2717 | 4483 |
| 7. | 2771 | 4549 |
| 8. | 35B1 | 6037 |
| 9. | 35B7 | 6043 |
| 10. | 35BB | 6047 |
| 11. | 3755 | 6257 |
| 12. | 377B | 6287 |
| 13. | 3B75 | 6857 |
| 14. | 5117 | 8803 |
| 15. | 5777 | 9739 |
| 16. | 27151 | 53773 |
| 17. | 31551 | 64717 |
| 18. | 315B5 | 64793 |
| 19. | 577BB | 116927 |
| 20. | 5B175 | 122921 |
| 21. | 5B1B7 | 122971 |
| 22. | 5B751 | 123757 |
| 23. | 75115 | 153953 |
| 24. | B7111 | 240349 |
| 25. | 255515 | 610721 |
| 26. | 255775 | 611081 |
| 27. | 2715B1 | 645397 |
| 28. | 27B177 | 662059 |
| 29. | 27B17B | 662063 |
| 30. | 3B515B | 983447 |
| 31. | 3B7B5B | 988343 |
| 32. | 51B717 | 1284931 |
| 33. | 575BBB | 1399679 |
| 34. | 577B75 | 1403081 |
| 35. | B71157 | 2884243 |
| 36. | 2715551 | 7743949 |
| 37. | 375B555 | 10823249 |
| 38. | 375B557 | 10823251 |
| 39. | 3771515 | 10847393 |
| 40. | 3B557B5 | 11808569 |
| 41. | 3B55B71 | 11809093 |
| 42. | 5771171 | 16818853 |
| 43. | 5771755 | 16819697 |
| 44. | 5B55BB1 | 17781109 |
| 45. | 5BB1711 | 17897917 |
| 46. | 7511151 | 22168717 |
| 47. | 7511157 | 22168723 |
| 48. | 27B7715B | 95460119 |
| 49. | 3B5155BB | 141615647 |
| 50. | 3B5157B7 | 141615931 |
| 51. | 3B557B75 | 141702857 |
| 52. | 3B55B7BB | 141709247 |
| 53. | 511B7755 | 182635121 |
| 54. | 5B55B1B5 | 213371993 |
| 55. | 27B771511 | 1145521309 |
| 56. | 27B771755 | 1145521649 |
| 57. | 375BB5B55 | 1558673201 |
| 58. | 3B5571515 | 1700416673 |
| 59. | 3B55B7755 | 1700510321 |
| 60. | 3B55B7B57 | 1700510899 |
| 61. | 375BB5B515 | 18704078369 |
Basis 13 mit 176 Fast Perfekten Primzahlen
(Perfekte Primzahlen sind fett gedruckt)
| n | Basis 13 | Dezimal |
|---|---|---|
| 1. | 2 | 2 |
| 2. | 3 | 3 |
| 3. | 5 | 5 |
| 4. | 7 | 7 |
| 5. | B | 11 |
| 6. | 23 | 29 |
| 7. | 25 | 31 |
| 8. | 2B | 37 |
| 9. | 32 | 41 |
| 10. | 34 | 43 |
| 11. | 38 | 47 |
| 12. | 52 | 67 |
| 13. | 56 | 71 |
| 14. | 58 | 73 |
| 15. | 76 | 97 |
| 16. | 7A | 101 |
| 17. | 7C | 103 |
| 18. | B6 | 149 |
| 19. | B8 | 151 |
| 20. | 232 | 379 |
| 21. | 236 | 383 |
| 22. | 23C | 389 |
| 23. | 256 | 409 |
| 24. | 2B6 | 487 |
| 25. | 2BA | 491 |
| 26. | 328 | 541 |
| 27. | 344 | 563 |
| 28. | 34A | 569 |
| 29. | 34C | 571 |
| 30. | 382 | 613 |
| 31. | 386 | 617 |
| 32. | 388 | 619 |
| 33. | 526 | 877 |
| 34. | 52A | 881 |
| 35. | 52C | 883 |
| 36. | 566 | 929 |
| 37. | 584 | 953 |
| 38. | 7A6 | 1319 |
| 39. | 7A8 | 1321 |
| 40. | B6C | 1949 |
| 41. | B8A | 1973 |
| 42. | 2324 | 4931 |
| 43. | 2326 | 4933 |
| 44. | 232A | 4937 |
| 45. | 2368 | 4987 |
| 46. | 23C2 | 5059 |
| 47. | 2566 | 5323 |
| 48. | 2B66 | 6337 |
| 49. | 2B6C | 6343 |
| 50. | 2BA6 | 6389 |
| 51. | 3286 | 7039 |
| 52. | 328A | 7043 |
| 53. | 3442 | 7321 |
| 54. | 344C | 7331 |
| 55. | 34CA | 7433 |
| 56. | 3886 | 8053 |
| 57. | 388C | 8059 |
| 58. | 526A | 11411 |
| 59. | 52C4 | 11483 |
| 60. | 52CA | 11489 |
| 61. | 52CC | 11491 |
| 62. | 5842 | 12391 |
| 63. | 584C | 12401 |
| 64. | 7A6C | 17159 |
| 65. | 7A8A | 17183 |
| 66. | B6C2 | 25339 |
| 67. | B6C6 | 25343 |
| 68. | B6CC | 25349 |
| 69. | B8A8 | 25657 |
| 70. | 23246 | 64109 |
| 71. | 232A6 | 64187 |
| 72. | 232A8 | 64189 |
| 73. | 23C2A | 65777 |
| 74. | 25664 | 69203 |
| 75. | 2B666 | 82387 |
| 76. | 2B66C | 82393 |
| 77. | 2B6C4 | 82463 |
| 78. | 2B6CA | 82469 |
| 79. | 2B6CC | 82471 |
| 80. | 2BA62 | 83059 |
| 81. | 2BA66 | 83063 |
| 82. | 32866 | 91513 |
| 83. | 328AC | 91571 |
| 84. | 34424 | 95177 |
| 85. | 344C8 | 95311 |
| 86. | 38864 | 104693 |
| 87. | 3886C | 104701 |
| 88. | 388C6 | 104773 |
| 89. | 388CC | 104779 |
| 90. | 52C48 | 149287 |
| 91. | 52CCA | 149393 |
| 92. | 58424 | 161087 |
| 93. | 5842A | 161093 |
| 94. | 584C8 | 161221 |
| 95. | 7A8A2 | 223381 |
| 96. | B6C2C | 329419 |
| 97. | B6C6C | 329471 |
| 98. | 23246C | 833429 |
| 99. | 232A62 | 834433 |
| 100. | 232A68 | 834439 |
| 101. | 232A8C | 834469 |
| 102. | 2B66CC | 1071121 |
| 103. | 2B6CA6 | 1072103 |
| 104. | 2B6CC6 | 1072129 |
| 105. | 2B6CCA | 1072133 |
| 106. | 2BA62A | 1079777 |
| 107. | 2BA62C | 1079779 |
| 108. | 2BA662 | 1079821 |
| 109. | 2BA66C | 1079831 |
| 110. | 328664 | 1189673 |
| 111. | 328AC6 | 1190429 |
| 112. | 344248 | 1237309 |
| 113. | 388642 | 1361011 |
| 114. | 38864C | 1361021 |
| 115. | 3886CA | 1361123 |
| 116. | 388C6A | 1362059 |
| 117. | 388CC4 | 1362131 |
| 118. | 52CCA2 | 1942111 |
| 119. | 52CCAC | 1942121 |
| 120. | 584248 | 2094139 |
| 121. | 5842AC | 2094221 |
| 122. | 7A8A26 | 2903959 |
| 123. | B6C2CA | 4282457 |
| 124. | B6C6C8 | 4283131 |
| 125. | 23246CC | 10834589 |
| 126. | 232A624 | 10847633 |
| 127. | 232A68C | 10847719 |
| 128. | 2B66CC4 | 13924577 |
| 129. | 2B66CC6 | 13924579 |
| 130. | 2B66CCA | 13924583 |
| 131. | 2B6CA6C | 13937351 |
| 132. | 2B6CC66 | 13937683 |
| 133. | 2B6CC6A | 13937687 |
| 134. | 2B6CCAC | 13937741 |
| 135. | 2BA62AC | 14037113 |
| 136. | 2BA62CC | 14037139 |
| 137. | 2BA6626 | 14037679 |
| 138. | 2BA66C6 | 14037809 |
| 139. | 328664C | 15465761 |
| 140. | 3886424 | 17693147 |
| 141. | 388C6A2 | 17706769 |
| 142. | 52CCA26 | 25247449 |
| 143. | 52CCAC8 | 25247581 |
| 144. | 5842484 | 27223811 |
| 145. | 7A8A266 | 37751473 |
| 146. | 7A8A26C | 37751479 |
| 147. | B6C2CA6 | 55671947 |
| 148. | B6C2CA8 | 55671949 |
| 149. | 23246CC2 | 140849659 |
| 150. | 2B66CC66 | 181019533 |
| 151. | 2B6CC66C | 181189891 |
| 152. | 2B6CC6A2 | 181189933 |
| 153. | 2BA62ACC | 182482481 |
| 154. | 2BA66266 | 182489833 |
| 155. | 388C6A24 | 230188001 |
| 156. | 388C6A26 | 230188003 |
| 157. | 7A8A26C4 | 490769231 |
| 158. | B6C2CA66 | 723735317 |
| 159. | B6C2CA6C | 723735323 |
| 160. | B6C2CA8A | 723735347 |
| 161. | 2B66CC664 | 2353253933 |
| 162. | 2B66CC66C | 2353253941 |
| 163. | 2B6CC6A2C | 2355469141 |
| 164. | 2BA66266A | 2372367839 |
| 165. | 2BA66266C | 2372367841 |
| 166. | 388C6A26C | 2992444051 |
| 167. | 7A8A26C46 | 6380000009 |
| 168. | B6C2CA668 | 9408559129 |
| 169. | B6C2CA66C | 9408559133 |
| 170. | B6C2CA6C2 | 9408559201 |
| 171. | B6C2CA6C8 | 9408559207 |
| 172. | B6C2CA8A8 | 9408559519 |
| 173. | 388C6A26C6 | 38901772669 |
| 174. | B6C2CA66C2 | 122311268731 |
| 175. | B6C2CA66CC | 122311268741 |
| 176. | B6C2CA8A8A | 122311273757 |
Es gibt 61 Perfekte Primzahlen zur Basis 13
| n | Basis 13 | Dezimal |
|---|---|---|
| 1. | 76 | 97 |
| 2. | 7C | 103 |
| 3. | 34A | 569 |
| 4. | 382 | 613 |
| 5. | 386 | 617 |
| 6. | 52A | 881 |
| 7. | 566 | 929 |
| 8. | 2326 | 4933 |
| 9. | 2368 | 4987 |
| 10. | 34CA | 7433 |
| 11. | 526A | 11411 |
| 12. | 52CA | 11489 |
| 13. | 7A6C | 17159 |
| 14. | B6CC | 25349 |
| 15. | B8A8 | 25657 |
| 16. | 23C2A | 65777 |
| 17. | 25664 | 69203 |
| 18. | 2B666 | 82387 |
| 19. | 2B6C4 | 82463 |
| 20. | 344C8 | 95311 |
| 21. | 52C48 | 149287 |
| 22. | 584C8 | 161221 |
| 23. | 232A8C | 834469 |
| 24. | 328AC6 | 1190429 |
| 25. | 344248 | 1237309 |
| 26. | 38864C | 1361021 |
| 27. | 3886CA | 1361123 |
| 28. | 388CC4 | 1362131 |
| 29. | 5842AC | 2094221 |
| 30. | B6C6C8 | 4283131 |
| 31. | 232A624 | 10847633 |
| 32. | 232A68C | 10847719 |
| 33. | 2B66CC4 | 13924577 |
| 34. | 2B66CCA | 13924583 |
| 35. | 2B6CA6C | 13937351 |
| 36. | 2B6CCAC | 13937741 |
| 37. | 2BA62CC | 14037139 |
| 38. | 2BA66C6 | 14037809 |
| 39. | 328664C | 15465761 |
| 40. | 3886424 | 17693147 |
| 41. | 52CCA26 | 25247449 |
| 42. | 52CCAC8 | 25247581 |
| 43. | 5842484 | 27223811 |
| 44. | 7A8A266 | 37751473 |
| 45. | 23246CC2 | 140849659 |
| 46. | 2B6CC66C | 181189891 |
| 47. | 2BA62ACC | 182482481 |
| 48. | 388C6A24 | 230188001 |
| 49. | 2B66CC664 | 2353253933 |
| 50. | 2B66CC66C | 2353253941 |
| 51. | 2B6CC6A2C | 2355469141 |
| 52. | 2BA66266A | 2372367839 |
| 53. | 2BA66266C | 2372367841 |
| 54. | 7A8A26C46 | 6380000009 |
| 55. | B6C2CA668 | 9408559129 |
| 56. | B6C2CA6C2 | 9408559201 |
| 57. | B6C2CA6C8 | 9408559207 |
| 58. | 388C6A26C6 | 38901772669 |
| 59. | B6C2CA66C2 | 122311268731 |
| 60. | B6C2CA66CC | 122311268741 |
| 61. | B6C2CA8A8A | 122311273757 |
Dreiecksberechnung
Siehe auch: Dreieck
| Umfang: | |
| Inkreisradius: | |
| Umkreisradius: | |
| Höhenformeln: | |
| Flächeninhalt: |
|
| nach a umgestellt | |
| Heronsche Flächenformel: wobei ist | |
| Vollständige Flächenformel: | |
| Flächenschwerpunkt: |
|
Fakultät
Die Fakultät ist in der Mathematik eine Funktion, die einer natürlichen Zahl das Produkt aller natürlichen Zahlen kleiner oder gleich dieser Zahl zuordnet. Sie wird durch ein dem Argument nachgestelltes Ausrufezeichen („!“) abgekürzt.
Es gibt eine auffällige Beziehung zwischen einigen Quadratzahlen und Fakultäten.
- 5^2-1 = 24 = 4!
- 11^2-1 = 120 = 5!
- 71^2-1 = 5040 = 7!
Fakultäten und Primzahlen
Bis auf die Zahl 2 = 2! müssen alle größeren Fakultäten zusammengesetzte Zahlen sein, denn sie sind Produkte der natürlichen Zahlen. Wie sieht es aber mit den Fakultäten +1 aus?
- 1!+1 = 2 = prim
- 2!+1 = 3 = prim
- 3!+1 = 7 = prim
- 4! und 5! (siehe oben)
- 6!+1 = 721 = 7*103
- 7! (siehe oben)
- 8!+1 = 40321 = 61*661
- 9!+1 = 362881 = 19*71*269
- 10!+1 = 3628801 = 11*329891
- 11!+1 = 39916801 = prim
- 12!+1 = 479001601 = 13^2*2834329
- 13!+1 = 6227020801 = 83*75024347
Weblinks
Downloads
Kosmische Geschwindigkeiten
Auszug aus der Disk zu Neutronenstern:
„Hier einmal die relevanten Werte und Formeln:
Radius Sonne
Masse Sonne
Radius Sonne als Neutronenstern:
Fluchtgeschwindigkeit an der Oberfläche des Neutronensterns
Sonnenmasse als Schwarzes Loch:
Lichtgeschwindigkeit
-- Zumthie 17:43, 1. Feb. 2012 (CET)
“
Kreisbahngeschwindigkeit
Masse Erde:
Äquatordurchmesser:
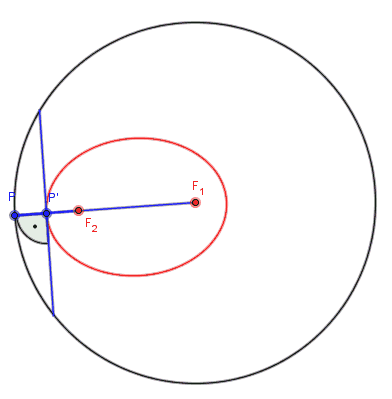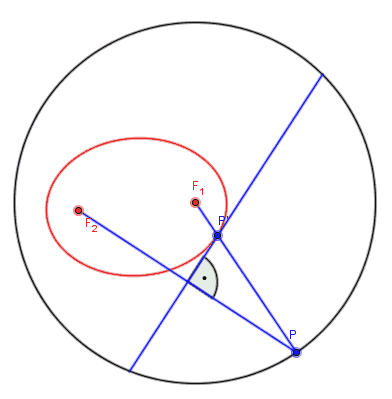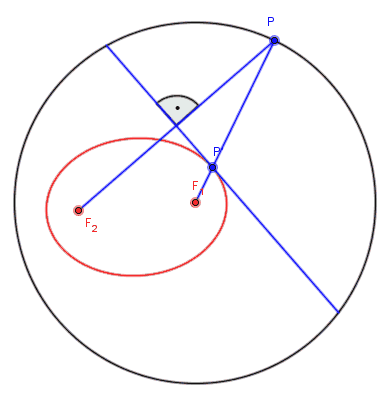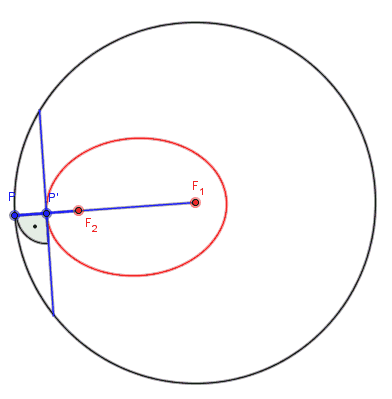
Ellipsenkonstruktion
Ellipsenkonstruktion nach Richard Feynman
Siehe auch: Feynmans verschollene Vorlesung: Die Bewegung der Planeten um die Sonne
Hypotenusenvierecke
Spezielle Sehnenvierecke
Goldener Schnitt im Hypotenusenquadrat
Goldener Schnitt fraktal