Schumann-Resonanz
Als Schumann-Resonanz (benannt nach dem deutschen Physiker und Elektroingenieur Winfried Otto Schumann) bezeichnet man das Phänomen, dass elektromagnetische Wellen bestimmter Frequenzen entlang des Umfangs der Erde stehende Wellen bilden. Die ausreichend leitfähige Erdoberfläche (größtenteils Salzwasser) und die gut leitfähige Ionosphäre darüber begrenzen einen kugelschalenförmigen Hohlraumresonator, aus dessen Abmessungen sich mögliche Resonanzfrequenzen berechnen lassen. Diese können durch Blitze angeregt werden, sind aber von so geringer Amplitude, dass sie nur mit sehr empfindlichen Instrumenten nachgewiesen werden können.
Berechnung der Frequenzen
Der mittlere Erdumfang beträgt a = 39.985.427 m (am Äquator 40.075 km, Polumfang 39.940 bzw. 40.007,863 km). Bei einer Ausbreitungsgeschwindigkeit des Lichts von c = 299.792.458 m/s (im Vakuum) ergeben sich für den mittleren Erdumfang dabei rechnerisch c/a = 7,5 Hz für die niedrigste Frequenz. Für einen Hohlraumresonator mit ideal leitenden Wänden führen genauere Berechnungen (siehe Literatur: Jackson, Elektrodynamik) auf die Formel:
für die n-te Frequenz (mit n = 1, 2, 3 …).
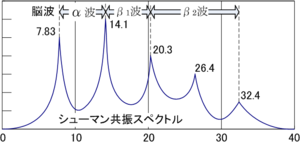
Da die Erde aber keine ideal leitenden Wände besitzt, muss obige Formel für die beobachteten Werte mit 0,78 multipliziert werden und führt dann für n = 1, 2, 3 … auf 7,83 (fundamental),[1] 14,3; 20,8; 27,3 und 33,8 Hz.[2][3] Durch Dispersion, Ionosphäreneffekte und andere nicht-ideale Eigenschaften des Systems weichen die Messwerte geringfügig von den theoretischen Werten ab und schwanken abhängig von den Jahreszeiten. Schumann-Resonanzfrequenzen von 3 Hz bis 30 Hz gehören in den Frequenzbereich, der international als Extremely Low Frequency bezeichnet wird.
Anregung
Durch Blitze und andere Vorgänge wird in der Atmosphäre und der Ionosphäre ein breites Spektrum elektromagnetischer Wellen ausgesendet, die auch als Sferics bezeichnet werden. Niederfrequente Wellen breiten sich hauptsächlich in der nur wenig leitfähigen Atmosphäre zwischen dem Erdboden und der Ionosphäre aus, die beide elektrisch ausreichend gut leiten. Wellen, die sich nach einer Erdumrundung wieder in der gleichen Phase befinden (d. h. der Erdumfang ist ein ganzzahliges Vielfaches der Wellenlänge) werden verstärkt, andere löschen sich aus. Dadurch ergibt sich eine tiefste Resonanzfrequenz von durchschnittlich etwa 7,8 Hz.
Entdeckung
Das Phänomen wurde 1952 von Winfried Otto Schumann und Herbert L. König entdeckt und 1960 experimentell untersucht.[4] Bereits früher war die Existenz derartiger Resonanzen postuliert und u. a. von Nikola Tesla beschrieben worden, ohne dass dieser sie allerdings systematisch einzuordnen vermochte. In einer Serie von Artikeln in den Jahren 1952 bis 1957 schließlich behandelte Schumann das Phänomen unter Berücksichtigung von Dämpfung und Anregung der Resonanzen durch Blitze weiter.
Die elektromagnetischen Wellen werden lokal leicht durch künstlich erzeugte Wechselfelder verdeckt. Bei der Vermessung des Frequenzspektrums in diesem niederfrequenten Bereich kann man auch stärkere künstlich erzeugte Wellen beobachten, z. B. die Frequenzen des europäischen und des amerikanischen Stromnetzes (50 Hz bzw. 60 Hz) und amerikanischer bzw. russischer U-Boot-Kommunikationssysteme (76 Hz bzw. 82 Hz).
Siehe auch
Literatur
- Kristian Schlegel, Martin Füllekrug: Weltweite Ortung von Blitzen: 50 Jahre Schumann-Resonanzen. Physik in unserer Zeit 33(6), 2002, ISSN 0031-9252, S. 256–261.
- John David Jackson: Klassische Elektrodynamik. 4. Auflage. Gruyter, Berlin 2005, ISBN 978-3-11-018970-4.
Weblinks
- Frequenz Monitor: Schumann Resonanz Frequenz Monitor
- A description of a homebrew ELF magnetic field detector experiment
- Magnetic activity and Schumann resonance
- Laufende Messung: Schumann resonances online
Einzelnachweise
- ↑ Can Resonant Oscillations of the Earth Ionosphere Influence the Human Brain Biorhythm? - V.D. Rusov, Department of Theoretical and Experimental Nuclear Physics, Odessa National Polytechnic University, Ukraine
- ↑ The electrical nature of storms By D. R. MacGorman, W. D. Rust, W. David Rust. Page 114.
- ↑ Recent advances in multidisciplinary applied physics By A. Méndez-Vilas. Page 65.
- ↑ R. Barra, D. Llanwyn Jones, C. J. Rodger (2000): ELF and VLF radio waves in Journal of Atmospheric and Solar-Terrestrial Physics 62, Elsevier