Logistische Regression

Unter logistischer Regression oder Logit-Modell versteht man in der Statistik Regressionsanalysen zur (meist multiplen) Modellierung der Verteilung abhängiger diskreter Variablen. Wenn logistische Regressionen nicht näher als multinomiale oder geordnete logistische Regressionen gekennzeichnet sind, ist zumeist die binomiale logistische Regression für dichotome (binäre) abhängige Variablen gemeint. Die unabhängigen Variablen können dabei ein beliebiges Skalenniveau aufweisen, wobei diskrete Variablen mit mehr als zwei Ausprägungen in eine Serie binärer Dummy-Variablen zerlegt werden.

Im binomialen Fall liegen Beobachtungen der Art $(y_{i};x_{i1},x_{i2},\ldots ,x_{ik}),\,i=1,\ldots ,n$ vor, wobei $Y_{i}$ eine binäre abhängige Variable (den so genannten Regressanden) bezeichnet, die mit $\mathbf {x} _{i}^{\top }$, einem bekannten und festen Kovariablenvektor von Regressoren, auftritt. $n$ bezeichnet die Anzahl der Beobachtungen. Das Logit-Modell ergibt sich aus der Annahme, dass die Fehlerterme unabhängig und identisch Gumbel-verteilt sind. Eine Erweiterung der logistischen Regression stellt die ordinale logistische Regression dar; eine Variante dieser ist das kumulative Logit-Modell.

Motivation

Logistische Funktion

Die Einflüsse auf diskrete Variablen können nicht mit dem Verfahren der klassischen linearen Regressionsanalyse untersucht werden, da wesentliche Anwendungsvoraussetzungen, insbesondere eine Normalverteilung der Residuen und Homoskedastizität, nicht gegeben sind. Ferner kann ein lineares Regressionsmodell bei einer solchen Variablen zu unzulässigen Vorhersagen führen: Wenn man die beiden Ausprägungen der abhängigen Variablen mit 0 und 1 kodiert, so kann man zwar die Vorhersage eines linearen Regressionsmodells als Vorhersage der Wahrscheinlichkeit auffassen, dass die abhängige Variable den Wert 1 annimmt – formal: $\mathrm {P} (Y_{i}=1)$ –, doch kann es dazu kommen, dass Werte außerhalb dieses Bereichs vorhergesagt werden. Die logistische Regression löst dieses Problem durch eine geeignete Transformation des Erwartungswerts der abhängigen Variablen $\mathrm {P} (Y_{i}=1)$.

Die Relevanz des Logit-Modells wird auch dadurch deutlich, dass Daniel McFadden und James Heckman im Jahr 2000 für ihren Beitrag zu seiner Entwicklung den Alfred-Nobel-Gedächtnispreis für Wirtschaftswissenschaften verliehen bekamen.

Anwendungsvoraussetzungen

Neben der Beschaffenheit der Variablen, wie sie in der Einleitung dargestellt wurde, gibt es eine Reihe von Anwendungsvoraussetzungen. So sollten die Regressoren keine hohe Multikollinearität aufweisen.

Modellspezifikation

Das (binomiale) logistische Regressionsmodell lautet

$\mathrm {P} (Y=1\mid X=x_{i})=\mathrm {P} (Y_{i}=1)={\frac {\exp(\mathbf {x} _{i}^{\top }{\boldsymbol {\beta }})}{1+\exp(\mathbf {x} _{i}^{\top }{\boldsymbol {\beta }})}}={\frac {1}{1+\exp(-\mathbf {x} _{i}^{\top }{\boldsymbol {\beta }})}}$,

hierbei stellt ${\boldsymbol {\beta }}$ den unbekannten Vektor der Regressionskoeffizienten dar ${\boldsymbol {\beta }}=(\beta _{0},\beta _{1},\ldots ,\beta _{k})^{\top }$ und das Produkt $\mathbf {x} _{i}^{\top }{\boldsymbol {\beta }}=\beta _{0}+x_{i1}\beta _{1}+x_{i2}\beta _{2}+\dotsc +x_{ik}\beta _{k}$ ist der lineare Prädiktor.

Es geht von der Idee der Chancen (englisch odds) aus, d. h. dem Verhältnis von $\mathrm {P} (Y_{i}=1)$ zur Gegenwahrscheinlichkeit $1-\mathrm {P} (Y_{i}=1)$ bzw. $\mathrm {P} (Y_{i}=0)$ (bei Kodierung der Alternativkategorie mit 0)

$\operatorname {Odds} (Y_{1/0}):={\frac {\mathrm {P} (Y_{i}=1)}{1-\mathrm {P} (Y_{i}=1)}}={\frac {\mathrm {P} (Y_{i}=1)}{\mathrm {P} (Y_{i}=0)}}.$

Die Chancen können zwar Werte größer 1 annehmen, doch ist ihr Wertebereich nach unten beschränkt (er nähert sich asymptotisch 0 an). Ein unbeschränkter Wertebereich wird durch die Transformation der Chancen in die sogenannten Logits

$\operatorname {Logit} (Y_{1/0}):=\ln(\operatorname {Odds} (Y_{1/0}))=\ln {\frac {\mathrm {P} (Y_{i}=1)}{1-\mathrm {P} (Y_{i}=1)}}$

erzielt; diese können Werte zwischen minus und plus unendlich annehmen. Die Logits dienen als eine Art Kopplungsfunktion zwischen der Wahrscheinlichkeit und dem linearen Prädiktor. In der logistischen Regression wird dann die Regressionsgleichung

$\operatorname {Logit} (Y_{1/0}\mid X_{i}=x_{i})=\beta _{0}+x_{i1}\beta _{1}+x_{i2}\beta _{2}+\dotsc +x_{ik}\beta _{k}$

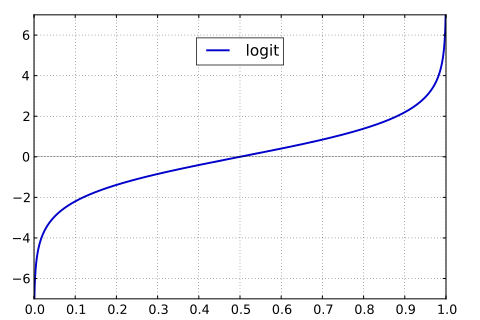
geschätzt; es werden also Regressionsgewichte bestimmt, nach denen die geschätzten Logits für eine gegebene Matrix von unabhängigen Variablen $X$ berechnet werden können. Die folgende Grafik zeigt, wie Logits (Ordinate) mit den Ausgangswahrscheinlichkeiten $\mathrm {P} (Y_{i}=1)$ (Abszisse) zusammenhängen:

Die Regressionskoeffizienten der logistischen Regression sind nicht einfach zu interpretieren. Daher bildet man häufig die sogenannten Effektkoeffizienten durch Exponenzieren; die Regressionsgleichung bezieht sich dadurch auf die Chancen:

$\operatorname {Odds} (Y_{1/0}\mid X_{i}=x_{i})=\exp(\beta _{0}+x_{i1}\beta _{1}+x_{i2}\beta _{2}+\dotsc +x_{ik}\beta _{k}).$

Die Koeffizienten $\exp(\beta _{j})$ werden oft auch als Effektkoeffizienten bezeichnet. Hier bezeichnen Koeffizienten kleiner 1 einen negativen Einfluss auf die Chancen, ein positiver Einfluss ist gegeben, wenn $\exp(\beta _{j})>1$.

Durch eine weitere Transformation lassen sich die Einflüsse der logistischen Regression auch als Einflüsse auf die Wahrscheinlichkeiten $\mathrm {P} (Y_{i}=1)$ ausdrücken:

$\mathrm {P} (Y=1\mid X_{i}=x_{i})={\frac {\exp(\beta _{0}+x_{i1}\beta _{1}+x_{i2}\beta _{2}+\dotsc +x_{ik}\beta _{k})}{1+\exp(\beta _{0}+x_{i1}\beta _{1}+x_{i2}\beta _{2}+\dotsc +x_{ik}\beta _{k})}}.$

Schätzmethode

Anders als bei der linearen Regressionsanalyse ist eine direkte Berechnung der besten Regressionskurve nicht möglich. Deshalb wird zumeist mit einem iterativen Algorithmus eine Maximum-Likelihood-Lösung geschätzt.

Modelldiagnose

Die Regressionsparameter werden auf der Grundlage des Maximum-Likelihood-Verfahrens geschätzt. Inferenzstatistische Verfahren stehen sowohl für die einzelnen Regressionskoeffizienten als auch für das Gesamtmodell zur Verfügung (siehe Wald-Test und Likelihood-Quotienten-Test); in Analogie zum linearen Regressionsmodell wurden auch Verfahren der Regressionsdiagnostik entwickelt, anhand derer einzelne Fälle mit übergroßem Einfluss auf das Ergebnis der Modellschätzung identifiziert werden können. Schließlich gibt es auch einige Vorschläge zur Berechnung einer Größe, die in Analogie zum Bestimmtheitsmaß ${\mathit {R}}^{2}$ der linearen Regression eine Abschätzung der „erklärten Variation“ erlaubt; man spricht hier von sogenannten Pseudo-Bestimmtheitsmaßen. Auch das Informationskriterium nach Akaike und das bayessche Informationskriterium werden in diesem Kontext gelegentlich herangezogen.

Insbesondere bei Modellen zur Risikoadjustierung wird häufig der Hosmer-Lemeshow-Test zur Bewertung der Anpassungsgüte verwendet. Dieser Test vergleicht die vorhergesagten mit den beobachteten Raten von Ereignissen in nach Auftretenswahrscheinlichkeit geordneten Untergruppen der Grundgesamtheit, häufig den Dezilen. Die Teststatistik wird wie folgt berechnet:

$H:=\sum _{g=1}^{n}{\frac {\left(O_{g}-E_{g}\right)^{2}}{N_{g}\pi _{g}(1-\pi _{g})}}.\,\!$

Dabei repräsentieren $O_{g}$ die beobachteten (englisch observed) Ereignisse, $E_{g}$ die erwarteten (englisch expected) Ereignisse, $N_{g}$ die Anzahl der Beobachtungen und $\pi _{g}$ die Auftretenswahrscheinlichkeit der gten Quantile. Die Anzahl der Gruppen beträgt $n$.

Ebenfalls wird die ROC-Kurve zur Beurteilung der Vorhersagekraft logistischer Regressionen verwendet, wobei die Fläche unter der ROC-Kurve (kurz: AUROC) als Gütekriterium fungiert.

Alternativen und Erweiterungen

Als (im Wesentlichen gleichwertige) Alternative kann das Probit-Modell herangezogen werden, bei dem eine Normalverteilung zugrunde gelegt wird.

Eine Übertragung der logistischen Regression (und des Probit-Modells) auf eine abhängige Variable mit mehr als zwei diskreten Merkmalen ist möglich (siehe Multinomiale logistische Regression oder Geordnete logistische Regression).

Literatur

• Hans-Jürgen Andreß, J.-A. Hagenaars, Steffen Kühnel: Analyse von Tabellen und kategorialen Daten. Springer, Berlin 1997, ISBN 3-540-62515-1.
• Dieter Urban: Logit Analyse. Lucius & Lucius, Stuttgart 1998, ISBN 3-8282-4306-1.
• David Hosmer, Stanley Lemeshow: Applied logistic regression. 2. Auflage. Wiley, New York 2000, ISBN 0-471-35632-8.
• Alan Agresti: Categorical Data Analysis. 2. Auflage. Wiley, New York 2002, ISBN 0-471-36093-7.
• Scott J. Long: Regression Models for Categorical and Limited Dependent Variables. Sage 1997, ISBN 0-8039-7374-8.

Weblinks

• Rede von Daniel McFadden zur Nobelpreisverleihung: Geschichte der Logit-Regression (englisch)
• Einführung in die Logistische Regression mit SPSS (PDF; 2,2 MB)