Diskussion:Kreuzprodukt

Diese Diskussionsseite dient dazu, Verbesserungen am Artikel „Kreuzprodukt“ zu besprechen. Persönliche Betrachtungen zum Thema gehören nicht hierher. Für allgemeine Wissensfragen gibt es die Auskunft.

Füge neue Diskussionsthemen unten an:

Klicke auf Abschnitt hinzufügen, um ein neues Diskussionsthema zu beginnen, und unterschreibe deinen Beitrag bitte mit oder --~~~~.

• Diskussionsregeln
• Hilfe zu Diskussionsseiten
• Sei sachlich und freundlich!
• Greife niemanden persönlich an!
• Geh von guten Absichten aus.

Zum Archiv

Auf dieser Seite werden Abschnitte ab Überschriftebene 2 automatisch archiviert, die seit 14 Tagen mit dem Baustein {{Erledigt|1=--~~~~}} versehen sind.

Der Name "äußeres Produkt"

Wieso heißt das Kreuzprodukt des Spezialfalls $\mathbb {R} ^{3}$ eigentlich "äußeres Produkt", während das Skalarprodukt als "inneres Produkt" bezeichnet wird? Mit äußerer und innerer Verknüpfung kann es nichts zu tun haben, sonst müsste man die Begrifflichkeiten umtauschen, auch wenn das Kreuzprodukt zweier "richtiger" Vektoren nur ein Pseudovektor ist.
Also, so stammen diese Bezeichnungen her?--Slow Phil (Diskussion) 19:30, 31. Okt. 2013 (CET)

Vermutlich gehen sie bis auf Hermann Graßmann zurück. --Digamma (Diskussion) 21:43, 29. Aug. 2016 (CEST)

Im englischen Sprachraum gibt es zwei Begriffe, die beide „äußeres“ Produkt übersetzt werden können: en:Outer product und en:Exterior product. Hier scheint mir letzterer gemeint, während ersterer den Begriff „inneres Produkt“ besser komplementiert (Skalarprodukt [inneres Produkt] $\mathbf {a} ^{\textsf {T}}\mathbf {b}$ und “outer product” $\mathbf {a} \mathbf {b} ^{\textsf {T}}$), z. B.

${\begin{bmatrix}4&5&6\end{bmatrix}}{\begin{bmatrix}2\\3\\-1\end{bmatrix}}=17$

bzw.

${\begin{bmatrix}2\\3\\-1\end{bmatrix}}\otimes {\begin{bmatrix}4&5&6\end{bmatrix}}={\begin{bmatrix}8&10&12\\12&15&18\\-4&-5&-6\end{bmatrix}}$.

--Erbschleicher (Diskussion) 19:16, 14. Mai 2022 (CEST)

Betragsstriche

Im Artikel steht bisher die Formel

$|{\vec {a}}\times {\vec {b}}|=|{\vec {a}}|\,|{\vec {b}}|\,\sin \theta \,.$

Diese wurde von 217.5.143.100 mit der Begründung

Der Betrag des Kreuzproduktes kann niemals negativ werden, er ist proportional zum Betrag des Sinus. Oder anders ausgedrückt liegt der Wertebereich des Winkels nur zwischen 0 und pi.

zu

$|{\vec {a}}\times {\vec {b}}|=|{\vec {a}}|\,|{\vec {b}}|\,|\sin \theta |\,$

geändert.

Dies ist natürlich alles richtig. Andererseits liegt der Winkel sowies zwischen 0 und $\pi$, da man im Raum keine orientierten Winkel definieren kann. Die Betragsstriche sind also richtig, aber überflüssig.

Frage: Welche Version ist besser? --Digamma (Diskussion) 11:23, 4. Aug. 2015 (CEST)

Welcher Winkel ist gemeint?

Grundsätzlich gibt es zwischen zwei Vektoren in der Ebene oder im Raum zwei Winkel, einen im Bereich $[0,\pi ]$ und einen im Bereich $[\pi ,2\pi ]$. Wenn von „dem Winkel zwischen zwei Vektoren“ gesprochen wird, ist per Konvention immer der erstere gemeint. Bei Berechnungen kann es jedoch durchaus vorkommen, dass man den zweiten erwischt. Da aber in der Literatur an dieser Stelle ausnahmslos auf die Betragsstriche verzichtet wird, sollten wir das auch so handhaben. Viele Grüße, --Quartl (Diskussion) 17:39, 4. Aug. 2015 (CEST)

Ist das so einheitlich? Im französischen Artikel stehen z. B. Betragsstriche. --Digamma (Diskussion) 18:05, 4. Aug. 2015 (CEST)

Ich habe ungefähr 20 deutsche Mathematik-Bücher auf Google Books gecheckt, alle ohne Betragsstriche. Viele Grüße, --Quartl (Diskussion) 18:22, 4. Aug. 2015 (CEST)

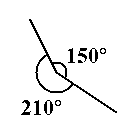
Ist auch richtig! Wie sieht denn ein Parallelogramm mit einem Innenwinkel von 210° aus? (nicht signierter Beitrag von 78.48.83.27 (Diskussion) 20:15, 9. Mai 2016 (CEST))

Hallo Digamma, nach meiner Kenntnis ist als Winkel zwischen zwei Vektoren derjenige gemeint, um den der erstgenannte Vektor im Gegenuhrzeigersinn gedreht werden muss, damit seine Richtung sich mit der des zweitgenannten deckt (steht, viel eleganter formuliert, irgendwo in meinen Lehrbüchern). Wenn also der in nebenstehender Abbildung nach rechts unten zeigende Vektor ${\vec {a}}$ sei, und der nach links oben zeigende Vektor ${\vec {b}}$, dann wäre für ${\vec {a}}\times {\vec {b}}$ mit einem Winkel von $\theta =150^{\circ }$ zu rechnen, und für ${\vec {b}}\times {\vec {a}}$ mit einem Winkel von $\theta =210^{\circ }$ – ihren Beträgen nach allerdings wären beide Kreuzprodukte als stets positive Quadratwurzeln ungeachtet ihrer entgegengesetzten Richtung gleich groß. Betragsstriche um den Sinus machen die Sache also auf jeden Fall "idiotensicherer". :-) --Qniemiec (Diskussion) 23:25, 13. Jan. 2020 (CET)

Von Uhrzeigersinn und Gegenuhrzeigersinn zu reden macht in der Ebene Sinn, aber nicht im Raum. Zwei Vektoren spannen immer eine Ebene auf, aber was darin Uhrzeiger- oder Gegenuhrzeigersinn sein soll, hängt davon ab, von welcher Seite man drauf schaut. Deshalb gibt es im Raum nur Winkel zwischen 0° und 180°. --Digamma (Diskussion) 23:43, 13. Jan. 2020 (CET)

Einleitung

Warum wird das Kreuzprodukt nicht als alternierende vektorwertige Bilinearform definiert? Das erspart euch viel Erklärungen. :-) (nicht signierter Beitrag von 78.48.83.27 (Diskussion) 20:15, 9. Mai 2016 (CEST))

Kurz: Weil den Artikel auch Nichtmathematiker verstehen sollen. Aber man kann eine alternative Definition als alternierende vektorwertige Bilinearform (die vermutlich noch gewisse Normierungsbedingungen erfüllen muss) zusätzlich einfügen. Eine Charakterisierung mit Hilfe der Determinante ist ja schon enthalten. --Digamma (Diskussion) 21:35, 9. Mai 2016 (CEST)

Lemma: Kreuzprodukt vs. Vektorprodukt

Auch wenn die Bezeichnung "Kreuzprodukt" sehr intuitiv ist, scheint mir der Name "Vektorprodukt" der "richtigere" zu sein. Ich schlage deshalb vor, den Artikel auf "Vektorprodukt" zu verschieben (und aus "Kreuzprodukt" eine Weiterleitung auf "Vektorprodukt" zu machen). Meinungen dazu? --Digamma (Diskussion) 20:50, 24. Okt. 2016 (CEST)

Puh, mir ist der Begriff Kreuzprodukt geläufiger. Wie kommst Du darauf, dass Vektorprodukt passender ist? Ich schlage eine Literaturrecherche vor. Grüße --Christian1985 (Disk) 21:32, 24. Okt. 2016 (CEST)

Zum Beispiel spricht der baden-württembergische Bildungsplan Mathematik Gymnasien Kursstufe von "Vektorprodukt". Ebenfalls das Schulbuch "Lambacher Schweizer Mathematik für Gymnasien Kursstufe Baden-Württemberg". Eine Google-Buch-Suche nach Vektorprodukt und nach Kreuzprodukt ergibt m.E. bessere Treffer für "Vektorprodukt". Auch der dtv-Atlas zur Mathematik spricht vom Vektorprodukt (und kennt "Kreuzprodukt" gar nicht). --Digamma (Diskussion) 09:54, 25. Okt. 2016 (CEST)

Ich denke, "Kreuzprodukt" macht die Sache auf jeden Fall kompatibler zum angelsächsischen Sprachgebrauch, wo es "cross product" genannt wird, im Gegensatz zu dem bei uns "Skalarprodukt" genannten "dot product". Das Problem ist dabei allerdings zu einem Gutteil auch ein sprachliches, denn beides sind ja "Produkte von Vektoren", für die sich kürzer auch der Überbegriff "Vektorprodukte" anböte – und da unterscheidet man im Englischen halt nach dem Rechenzeichen, also Kreuz oder Punkt, so dass der Ausdruck "vector products" als zusammenfassender Überbegriff verwendbar bleibt, während wir im Deutschen nach dem Ergebnis dieser Multiplikation, also Vektor oder Skalar, unterscheiden und damit "Vektorprodukte" nicht mehr so ohne weiteres als Überbegriff zur Verfügung steht. Was es auch im Unterricht nicht leichter macht, weil "Skalarprodukt" damit nicht etwa das Produkt zweier Skalare ist, sondern ein Skalar als Multiplikations-Produkt, während das "Vektorprodukt" ein Vektor als Multiplikations-Produkt zweier Vektoren ist. Wenn also das "Punktprodukt" hier "Skalarprodukt" genannt wird, sollte das "Kreuzprodukt" konsequenterweise auch "Vektorprodukt" heißen, und umgekehrt. Am besten freilich ist es, man weist stets auf beide Bezeichnungsmöglichkeiten hin, schon, weil die Leser vielleicht irgendwann auch mal ein englisches Lehrbuch zu Rat ziehen wollen. --Qniemiec (Diskussion) 00:00, 14. Jan. 2020 (CET)

Aus dem Schul- und Univ.Unterricht, der bei mir schon länger zurückliegt, kenne ich nur die Begriffe Skalarprodukt und Vektorprodukt. Kreuzprodukt habe ich erst hier bei WP gelesen. Kreuzprodukt nur des Kreuzes wegen müsste dann konsequenterweise Punktprodukt statt Skalarprodukt bedeuten. Beide begriffe klingen etwas unbeholfen, so wie Malnehmen für Multiplizieren oder Tuwort und Wiewort statt Verb und Adjektiv. --Dioskorides (Diskussion) 23:33, 6. Feb. 2020 (CET)

Ich stimme mit Digamma und Dioskorides überein, obwohl mir die pragmatischen Worte Kreuz- und Punkt- auch gefallen. Wir des Alten Gewohnten werden bald aussterben, und unsere papierenen Lehr- und Nachschlagebücher außer Gebrauch kommen. Deshalb wird wohl Qniemiec über kurz oder lang bestätigt werden. Ist doch das Verhältnis der Trefferzahl bei Google-Suche (als halbenglisches Wort im Deutschen längst etabliert und zum meist gebrauchten Rechercheinstrument längst avanciert) jetzt schon 3:2 zu Gunsten von Kreuz-.
-- mfGn Ana Lemma 37 12:13, 7. Feb. 2020 (CET)

Abschnitt Beziehung zur Determinante präzisieren

Obwohl es um die Charakterisierung des Kreuzprodukts geht, ist hier ein beliebiges Spatprodukt definiert (beliebiges v). Vorschlag daher Vektor v mit Basisvektor e zu ersetzen, welcher in der folgenden Gleichung quasi als neutrales Element fungiert: ${\vec {a}}\times {\vec {b}}={\vec {e}}\cdot ({\vec {a}}\times {\vec {b}})=({\vec {a}}\times {\vec {b}})\cdot {\vec {e}}=\det({\vec {e}},{\vec {a}},{\vec {b}})$ So steht da natürlich immer noch ein Spatprodukt, der Fokus liegt aber auf dem Kreuzprodukt und der Satz zum zitierten Herbert Amann macht auch Sinn. Gedanken dazu?(nicht signierter Beitrag von Robsedropse (Diskussion | Beiträge) 10:11, 28. Feb. 2017 (CET))

Ich verstehe nicht, warum es dich stört, dass von einem beliebigen v die Rede ist. Die Idee ist doch, dass die beiden Linearformen ${\vec {v}}\mapsto \det({\vec {v}},{\vec {a}},{\vec {b}})$ und ${\vec {v}}\mapsto v\cdot ({\vec {a}}\times {\vec {b}})$ übereinstimmen. Das tun sie natürlich, wenn sie auf einer Basis übereinstimmen. Aber dies ist kein Grund, sich auf eine Basis zu beschränken.

Das mit dem "neutralen Element" ist m.E. Unsinn. Die Gleichung ${\vec {a}}\times {\vec {b}}={\vec {e}}\cdot ({\vec {a}}\times {\vec {b}})$ ist falsch und ergibt keinen Sinn, denn links vom Gleichheitszeichen steht ein Vektor, rechts davon aber eine Zahl. --Digamma (Diskussion) 16:13, 28. Feb. 2017 (CET)

Ich habe mich gefragt wie man den Abschnitt verbessern könnte, daher der Vorschlag. Ok ich hatte nicht verstanden, dass es gerade Linearformen mit beliebigem Vektor v sind, die hervorgehoben werden sollen. Das Gleichheitszeichen scheint gewagt und gilt nur mit dem Kunstgriff $\textstyle {\vec {e}}={\begin{pmatrix}{\vec {e}}_{1}\\{\vec {e}}_{2}\\{\vec {e}}_{3}\end{pmatrix}}$ - ähnlich wie man die Determinante künstlich aufbläht - , stiftet aber in Bezug auf das Skalarprodukt wohl mehr Verwirrung als ich aufzulösen versuchte. Einen echten Bezug zur Determinante hat eben das Spatprodukt und den Hinweis gibt es nun.

--Robsedropse (Diskussion) 23:16, 28. Feb. 2017 (CET)

Dinge die die Welt nicht braucht

"Polare und axiale Vektoren", "in der Physik spielt es eine Rolle...", so einen Unsinn habe ich noch selten gehört. Vektoren der Physik und Vektoren der Mathematik sind dasselbe. Diese Einteilung ist typisch für laisches Unverständnis der Mathematik. Das ist Pseudowissenschaft. Niemand braucht in der Mathematik die Unterscheidung in "Polare und axiale Vektoren", also braucht sie auch niemand in der Physik, aus dem einfachen Grund weil es absolute Bezugsysteme nicht gibt. In einem bewegten Bezugsystem sind alle Vektoren polar, sonst gäbe es keine Präzession. Vektoren sind Vektoren. Die Signatur mag sich Ändern wie da beschrieben im Artikel, hat jedoch keine physikalische Bedeutung, nur ergibt sich das schlicht und einfach aus der Mathematik der Vektoren, ohne dazu diese Einteilung zu benötigen. Die Regel ist einfach nur pseudowissenschaftliche Eselsbrückenmathematik. Was soll man auch erwarten von einem Lexikon bei dem Hinz und Kunz mitschreiben dürfen.

Pseudovektoren sind nunmal keine Vektoren. Wenn man sich sie die Vorzeichen genauer anschaut, dann ist da ein Unterschied zu den normalen Vektoren. Insbesondere bei Symmetrietransformationen. Wenn A×B=C gilt, dann gilt (-A)×(-B)=C und nicht (-C), was bei Punktinversion herauskäme. Also ist C entweder Null oder eben kein klassischer Vektor. --Boehm (Diskussion) 08:02, 1. Okt. 2017 (CEST)

rechtsassoziativ?

In [1], S. 10, wird für das Kreuzprodukt als "Unser Standard" Rechtsassoziativität gesetzt. Ich vermute, das ist allgemeine Konvention, denn

• Die Jacobi-Identität und die Graßmann-Identität werden üblicherweise "rechts geklammert" hingeschrieben.
• In [2] hat in Gl. 2.8b ein Term $a\times a\times b$ keine Klammer, verschwindet aber nicht.

Hat jemand eine Buchquelle dafür? --Rainald62 (Diskussion) 12:53, 8. Aug. 2018 (CEST)

Ich habe noch nie Terme mit mehreren Kreuzprodukten gesehen, die nicht geklammert waren. Ich glaube nicht, dass es unter Mathematikern eine Konvention gibt, wie solche Terme zu interpretieren sind. --Digamma (Diskussion) 12:58, 8. Aug. 2018 (CEST)

Klammern setzen ist schon deshalb gut, weil eine Konvention, falls es sie gäbe, reichlich unbekannt ist. Übrigens lässt sich in OOP-Sprachen bei der Operatorüberladung die Assoziativität nicht ändern, '*' bleibt linksassoziativ. Ein weiterer Grund, auf Klammern nicht zu verzichten. --Rainald62 (Diskussion) 13:27, 8. Aug. 2018 (CEST)

Ergänzung: In [3] geht es nicht um das Vektorprodukt, sondern um das kartesische Produkt. --Digamma (Diskussion) 13:02, 8. Aug. 2018 (CEST)

Zu schnell gelesen (der Abschnitt ist "Kreuzprodukt" überschrieben, und ich wusste nicht, dass auch das kartesische so bezeichnet wird). --Rainald62 (Diskussion) 13:27, 8. Aug. 2018 (CEST)

Nachgefragt: Hast du sonst schon mal die Zentripetalbeschleunigung in der Form ${\vec {\omega }}\times {\vec {\omega }}\times {\vec {r}}'$ geschrieben gesehen, ohne Klammern? --Digamma (Diskussion) 13:08, 8. Aug. 2018 (CEST)

Nein, allerdings auch noch nicht so: $({\vec {r}}\times {\vec {\omega }})\times {\vec {\omega }}$.

Du meinst also, selbst wenn es die Konvention gäbe, sollte sie nicht im Artikel stehen? --Rainald62 (Diskussion) 13:27, 8. Aug. 2018 (CEST)

Ja. --Digamma (Diskussion) 13:38, 8. Aug. 2018 (CEST)

Ok. --Rainald62 (Diskussion) 14:37, 8. Aug. 2018 (CEST)

multidimensionales Kreuzprodukt nochmal

Es gab auf dieser Seite in der Vergangenheit schon einmal eine Diskussion über die Anordnung der Argumente in der "Determinante" welche das verallgemeinerte Kreuzprodukt a₁ x a₂ x ... x a_n-1 definiert. Ausgang war, dass die aktuell im Artikel vertretene Anordnung die richtige ist, auch wenn der Ergebnisvektor in Räumen geradzahliger Dimension in die "falsche" Richtung zeigt (im R⁴ ist zum Beispiel e₁ x e₂ x e₃ = - e₄ und nicht + e₄, wenn e_i die Einheitsvektoren sind). Gleichzeitig wird darauf verwiesen, dass dieses Kreuzprodukt dasselbe ist wie der Hodge-Operator angewendet auf das äußere Produkt der Grassmann-Algebra. (Siehe auch Graßmann-Algebra#Beziehung_zum_Kreuzprodukt_und_Spatprodukt_(Hodge-Dualität_von_Vektoren)_und_Begriffen_der_Physik.)

Wenn ich mir zweitere Definition aber genauer ansehe, müsste doch wegen der Definition des Hodge-Operators im R⁴ *(e₁ Λ e₂ Λ e₃) = e₄ und damit e₁ x e₂ x e₃ = 1(eingeschlossenes Volumen) • *(e₁ Λ e₂ Λ e₃) = e₄ gelten? (Ich hoffe man kann erkennen was ich meine, meine eilig notierten Formeln hier sind ein wenig entstellt.)

Das gleiche Resultat bekomme ich auch, wenn ich vom Spatprodukt ausgehe, welches auch ein Spezialfall des äußeren Produkts ist. Im R³ ist a * b x c = blablabla • *(e₁ Λ e₂ Λ e₃), wobei der hintere Ausdruck = 1 ist. Wenn ich nun die Vektoren um eine vierte Komponente mit Wert 0 erweitere, wird der "Hodge-Ausdruck" = e₄. Nach der Formel in unserem Artikel kann ich außerdem das Kreuzprodukt a x b x c ausrechnen, das Resultat hiervon ist allerdings negativ (blablabla * (-e₄)), da e₄ an einer "negativen" Stelle in der Matrix steht.

Irgendwie verständlich? Sorry, bin kein Mathematikprofessor oder so, meine Ausdrucksweise ist daher auch wahrscheinlich nicht ganz formal korrekt. Worauf ich hinaus will, ist: Sicher dass die Spalte mit den Einheitsvektoren in der "Determinante" nach vorne und nicht nach hinten gehört? Letztere Variante wäre nach meiner Rechnung nämlich mit dem Hodge-Dualismus konsistent. Oder mache ich einen Denkfehler? --2003:E7:772C:6591:255E:A2D7:37EB:4C09 00:06, 24. Okt. 2018 (CEST)

Das klingt alles überzeugend. Und ich habe gerade gesehen, dass im englischsprachigen Artikel das verallgemeinerte Kreuzprodukt genau so definiert wird. Man müsste also Literatur suchen. Für die aktuelle Verions im Artikel habe ich nur eine Vorlesungsmitschrift zu bieten. --Digamma (Diskussion) 21:09, 24. Okt. 2018 (CEST)

Bin auch der Meinung der anderen IP - das Produkt gehört "natürlich" und intuitiv in die letzte Spalte! Speziell im R^2 nervt, dass der Resultatvektor nicht der im mathematisch positiven Sinn gedrehte Ausgangsvektor ist, also (-a_y, a_x). Privat benutze ich zwei Dualitätsoperatoren: ein D und ein umgedrehtes D (mit Doppellinie), die in Kombination die lästige Notierung von Vorzeichen der Art (-1)^(m(n-m)) ersparen. Nu ja.

--2A01:C22:3410:8A00:1D1B:423C:35F9:2349 02:03, 21. Jan. 2019 (CET)

Polare und axiale Vektoren

Text: "Bei der vektoriellen Multiplikation mit einem polaren Vektor b wechseln Vektoren ihre Signatur: Ist a ein polarer Vektor, so ist a × b ein axialer; ist a ein axialer Vektor, so ist a × b ein polarer. Bei der vektoriellen Multiplikation mit einem axialen Vektor bleibt dagegen die Signatur erhalten."

Diese Sprechweise ist erklärungsbedürftig. Die Sichtweise ist hier offenbar, einen der beiden Vektoren zusammen mit dem × als Operator zu betrachten, den anderen als Operanden, der ins Resultat transformiert wird und dabei verschiedene Eigenschaften ändert. Natürlich wechselt hier kein Vektor seine Signatur, gemeint ist, daß der Produktvektor eine andere Signatur hat als der als Operand betrachtete Vektor.

Ich ändere also zu: "Bei der vektoriellen Multiplikation zweier Vektoren multiplizieren sich ihre Signaturen: zwei Vektoren mit gleicher Signatur liefern ein axiales, zwei mit verschiedener Signatur ein polares Vektorprodukt. Operationell ausgedrückt: Ein Vektor überträgt seine Signatur auf des Kreuzprodukt mit einem anderen Vektor, wenn dieser axial ist; ist der andere Vektor dagegen polar, bekommt das Kreuzprodukt die entgegengesetzte Signatur." --2A01:C22:3410:8A00:1D1B:423C:35F9:2349 01:44, 21. Jan. 2019 (CET)

Leider bleibt unklar, was es mit der Signatur auf sich hat. Ist damit Signatur (Lineare Algebra) gemeint? Ändert das die Rechenregeln des Kreuzproduktes? Oder ist es nur eine Hintergrundinformation zur Bewertung des Ergebnisses?--Hfst (Diskussion) 07:51, 21. Feb. 2019 (CET)

Mit "Signatur" ist genau das gemeint, was im Satz darüber definiert wird: "Polaren Vektoren ordnet man die Signatur (oder Parität) +1 zu, axialen Vektoren die Signatur −1." Mit der im Artikel Signatur (Lineare Algebra) behandelten Signatur von Bilinearformen hat das nichts zu tun. Es ist nur eine Hintergrundinformation, die vor allem die Anwendungen in der Physik betrifft. Mit den Rechenregeln des Kreuzprodukts hat es nichts zu tun. --Digamma (Diskussion) 21:50, 21. Feb. 2019 (CET)

Leider immer noch unklar, denn das Kreuzprodukt zweier Schubvektoren ist ein Drehvektor; wenn die Signatur der ersten beiden also +1 ist und diese Signaturen sich beim Kreuzprodukt wie behauptet multiplizieren, müsste das Ergebnis ebenfalls die Signatur +1 und nicht -1 haben. --Qniemiec (Diskussion) 22:54, 13. Jan. 2020 (CET)

Da habe ich wohl nicht gründlich genug gelesen. Möglicherweise sind die beiden Vorzeichen einfach vertauscht, d.h. axiale Vektoren haben positive und polare haben negative Signatur? Würde es dann stimmen? Man bräuchte überhaupt eine Quelle für den Abschnitt. --Digamma (Diskussion) 23:38, 13. Jan. 2020 (CET)

Zweiter Absatz: "Das Kreuzprodukt der Vektoren und ist ein Vektor, der senkrecht auf der von den beiden Vektoren aufgespannten Ebene steht und mit ihnen ein Rechtssystem bildet.°

Ich empfehle, diesen Satz zu ergänzen damit er gedanklich leichter umgesetzt werden kann mit: "das heißt, ein Drehen des ersten Vektors in den zweiten ergibt die positive Richtung des dritten über den Rechtsschraubensinn." Diese Definition wird in den Ingenieurwissenschaften verwendet, da die Rechtsschraube im täglichen Umgang mit Geräten die Norm ist. Auch die Erdrotation definiert über den Rechtsschraubensinn die Ausrichtung der Drehachse Süd-Nord.

Die Rechte-Hand-Regel ist dagegen ein Krampf. Millionen von Schülerinnen verrenken sich die Finger, nur um damit in etwa klar zu kommen. Immer stellt sich die Frage über die Zuordnung der einzelnen Finger zu den Vektoren. Ich schlage vor, das Bild mit der rechten Hand (oder war das nicht doch die linke)durch eine Schraube zu ersetzen. Eine Schraube kann auch losgelöst vom menschlichen Körper in die vorliegende Situation eingebracht werden.--Rüdiger (Diskussion) 19:53, 4. Apr. 2019 (CEST)

In der Einleitung würde ich nicht genauer werden. Schließlich ist der Artikel "Rechtssystem" verlinkt. Was ein Rechtssystem ist, soll vornehmlich dort erklärt werden. Weiter unten im Text im Abschnitt "Geometrische Definition" wird es genauer ausgeführt:

Dieser Vektor ist so orientiert, dass ${\vec {a}},{\vec {b}}$ und ${\vec {a}}\times {\vec {b}}$ in dieser Reihenfolge ein Rechtssystem bilden. Mathematisch heißt das, dass die drei Vektoren ${\vec {a}},{\vec {b}}$ und ${\vec {a}}\times {\vec {b}}$ gleich orientiert sind wie die Vektoren ${\vec {e}}_{1}$, ${\vec {e}}_{2}$ und ${\vec {e}}_{3}$ der Standardbasis. Im physikalischen Raum bedeutet es, dass sie sich wie Daumen, Zeigefinger und abgespreizter Mittelfinger der rechten Hand verhalten (Rechte-Hand-Regel).

Meiner Meinung nach genügt das. Ich habe aber mal deinen Formulierungsvorschlag ergänzt:

Ein Drehen des ersten Vektors ${\vec {a}}$ in den zweiten Vektor ${\vec {b}}$ergibt die positive Richtung des Vektors ${\vec {a}}\times {\vec {b}}$ über den Rechtsschraubensinn.

Ich hoffe, das ist so OK. --Digamma (Diskussion) 22:53, 4. Apr. 2019 (CEST)

Multiplikation mit einem Skalar

Kann man bei der Eigenschaft Bilinearität die Multiplikation mit einem Skalar aufnehmen oder wäre es besser da einen neuen Unterpunkt zu erstellen?

$\lambda ({\vec {a}}\times {\vec {b}})=\lambda {\vec {a}}\times {\vec {b}}={\vec {a}}\times \lambda {\vec {b}}.$ (nicht signierter Beitrag von 132.199.53.20 (Diskussion) 13:40, 16. Sep. 2019 (CEST))

Du meinst wohl eine Ergänzung wie diese? Ja, das ist im Begriff "Bilinearität" enthalten, wie aus dem verlinkten Artikel Bilineare Abbildung hervorgeht, aber auch aus der ersten Gleichung mit γ=0, bzw. der zweiten Gleichung mit α=0. Ich habe es ergänzt. --Dogbert66 (Diskussion) 22:47, 16. Sep. 2019 (CEST)

(BK) Diese Eigenschaft ist im Prinzip in den dort genannten Gleichungen

${\begin{aligned}{\vec {a}}\times (\beta \,{\vec {b}}+\gamma \,{\vec {c}})=\beta \,({\vec {a}}\times {\vec {b}})+\gamma \,({\vec {a}}\times {\vec {c}})\,,\\(\alpha \,{\vec {a}}+\beta \,{\vec {b}})\times {\vec {c}}=\alpha \,({\vec {a}}\times {\vec {c}})+\beta \,({\vec {b}}\times {\vec {c}})\,.\end{aligned}}$

enthalten:

Setzt man ${\vec {b}}={\vec {0}}$, so erhält man aus der ersten Gleichung ${\vec {a}}\times (\gamma \,{\vec {c}})=\gamma \,({\vec {a}}\times {\vec {c}})$ und aus der zweiten Gleichung $(\alpha \,{\vec {a}})\times {\vec {c}}=\alpha \,({\vec {a}}\times {\vec {c}})$.

Mir gefällt es aber auch besser, wenn die Additivität und die Homogenität getrennt formuliert werden. Magst du das umsetzen? --Digamma (Diskussion) 22:50, 16. Sep. 2019 (CEST)

Danke, so hab ich das gemeint. (nicht signierter Beitrag von 132.199.53.20 (Diskussion)) 13:23, 18. Sep. 2019 (CEST)

Kreuzprodukt in komplexwertigen Vektorräumen

Hallo,

es wäre super, wenn für den Abschnitt noch Quellen nachgetragen werden. --Christian1985 (Disk) 17:21, 11. Jan. 2022 (CET)

Herleitung

Ich finde, man sollte noch die Herleitung hinzufügen. Hier ein Video dazu https://www.youtube.com/watch?v=T__-xcGLTXs --HobbyAstronaut (Diskussion) 18:31, 3. Aug. 2022 (CEST)(Diskussion) 18:29, 3. Aug. 2022 (CEST)

Im mathematischen Sinn ist das keine Herleitung, sondern nur eine Motivation. Das Video zeigt, wie man mit Hilfe des LGS einen Vektor findet, der auf den zwei gegebenen Vektoren orthogonal steht. Aber warum man gerade diese spezielle Lösung nimmt, wird nicht klar. --Digamma (Diskussion) 23:36, 3. Aug. 2022 (CEST)