Sedimentationsgeschwindigkeit
Unter der Sedimentations-, Sink- oder Absinkgeschwindigkeit (auch Absinkrate) versteht man die Vertikalgeschwindigkeit, mit der sich ein Partikel innerhalb eines fluiden Mediums absetzt (sedimentiert). Wichtig ist diese vor allem für Korngrößenanalysen und die damit verbundenen mechanischen Trennverfahren (Zentrifugation, Dichtegradientenzentrifugation, Dekantieren, Sedimentation).
Vor allem in der Biologie wird die Sedimentationsgeschwindigkeit in Svedberg angegeben.[1]
Berechnung
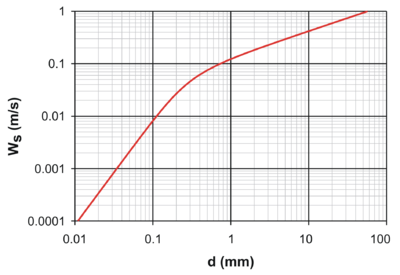
die Kurve zeigt unterschiedliche Bereiche, da sich mit dem Korndurchmesser die Reynoldszahl und damit auch die Formel für den Drag Coefficient ändert
Die Sedimentationsgeschwindigkeit bleibt im Falle einer rein gravitativen Sedimentation (d. h. ohne Zentrifugation) konstant, sobald die mit der Geschwindigkeit zunehmende Reibungskraft die Gravitationskraft kompensiert, welche das Partikel beschleunigt.
Bei der Berechnung wird von kugelförmigen Teilchen ausgegangen, die in einer unendlich ausgedehnten Flüssigkeit sedimentieren, bei der weder Wände noch Nachbarteilchen die Geschwindigkeit beeinflussen:[2]
Die Sedimentationsgeschwindigkeit hängt ab von:[3]
- der Dichte ρp des Partikels und der Dichte ρf des Fluids
- der Schwerebeschleunigung g
- dem Durchmesser bzw. Äquivalentdurchmesser d des Partikels
- dem Strömungswiderstandskoeffizient (Drag Coefficient) CD.
- mit der dort enthaltenen Viskosität des Fluids (s. u.)
Der Strömungswiderstandskoeffizient CD hängt wiederum ab von der Reynolds-Zahl :
- für geringe Sedimentationsgeschwindigkeiten bzw. Reynolds-Zahlen (Re < 0,5; laminare Strömung) gilt CD=24/Re. In diesem Fall ist die Sedimentationsgeschwindigkeit mit der Stokesschen Gleichung berechenbar, sie ändert sich mit dem Quadrat des Partikelradius bzw. des Äquivalentdurchmessers.[2]
- zwischen diesen beiden Bereichen (0,5 < Re < 1000) gibt es keine einfache Formel für CD, aber verschiedene empirische Formeln, z. B. CD=18,5/Re0,6.[2]
- für hohe Sedimentationsgeschwindigkeiten bzw. Reynolds-Zahlen (1000 < Re < 200.000, Newton-Bereich) gilt CD=0,44 (für Kugeln). In diesem Fall ändert sich die Sedimentationsgeschwindigkeit mit der Wurzel des Partikelradius bzw. des Äquivalentdurchmessers, siehe Formel oben. Es liegt eine turbulente Strömung vor.[2]
Als allgemeine Näherung für den Stokes-, Übergangs- und Newton-Bereich kann folgende Formel angewendet werden[2]:
Einzelnachweise
- ↑ Peter C. Heinrich, Matthias Müller, Lutz Graeve: Löffler/Petrides Biochemie und Pathobiochemie. Springer-Verlag, 2014, ISBN 978-3-642-17972-3, S. 92 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ a b c d e Klaus Luckert: Handbuch der mechanischen Fest-Flüssig-Trennung. Vulkan-Verlag GmbH, 2004, ISBN 3-8027-2196-9, S. 106 (eingeschränkte Vorschau in der Google-Buchsuche).
- ↑ Ralf Takors: Kommentierte Formelsammlung Bioverfahrenstechnik. Springer-Verlag, 2014, ISBN 978-3-642-41903-4, S. 118 (eingeschränkte Vorschau in der Google-Buchsuche).




