Bayessches Netz

Ein bayessches Netz oder Bayes’sches Netz (benannt nach Thomas Bayes) ist ein gerichteter azyklischer Graph (DAG), in dem die Knoten Zufallsvariablen und die Kanten bedingte Abhängigkeiten zwischen den Variablen beschreiben. Jedem Knoten des Netzes ist eine bedingte Wahrscheinlichkeitsverteilung der durch ihn repräsentierten Zufallsvariable, gegeben die Zufallsvariablen an den Elternknoten, zugeordnet. Sie werden durch Wahrscheinlichkeitstabellen beschrieben. Diese Verteilung kann beliebig sein, jedoch wird häufig mit diskreten oder Normalverteilungen gearbeitet. Eltern eines Knotens v sind diejenigen Knoten, von denen eine Kante zu v führt.

Ein bayessches Netz dient dazu, die gemeinsame Wahrscheinlichkeitsverteilung aller beteiligten Variablen unter Ausnutzung bekannter bedingter Unabhängigkeiten möglichst kompakt zu repräsentieren. Dabei wird die bedingte (Un)abhängigkeit von Untermengen der Variablen mit dem A-priori-Wissen kombiniert.

Sind X₁, …, X_n einige der im Graphen vorkommenden Zufallsvariablen (die abgeschlossen sind unter Hinzufügen von Elternvariablen), so berechnet sich deren gemeinsame Verteilung als

$P(X_{1},\dots ,X_{n})=\prod _{i=1}^{n}P(X_{i}|\mathrm {Eltern} (X_{i}))\;.$

Dabei ist $P(X_{1},\dots ,X_{n})$ eine symbolische Schreibweise für die gemeinsame Wahrscheinlichkeitsverteilung der Zufallsvariablen $X_{1},\dots ,X_{n}$. Hat ein Knoten keine Eltern, so handelt es sich bei der assoziierten Wahrscheinlichkeitsverteilung um eine unbedingte Verteilung.

Wie im Beispiel unten, interessiert man sich häufig für eine Randwahrscheinlichkeit, die man durch Marginalisierung über alle möglichen Realisierungen $x_{j}$ im Zustandsraum $E_{j}$ der Zufallsvariable $X_{j}$ erhält:

$P(X_{1}=x_{1})=\sum _{x_{2}\in E_{2}}\dots \sum _{x_{n}\in E_{n}}P(X_{1}=x_{1},\dots ,X_{n}=x_{n}).$

Beispiel

Beispiel für ein bayessches Netz mit drei Knoten und zwei Kanten. In den Tabellen sind oben links die Werte der Wahrscheinlichkeitsfunktion $P(W)$, rechts die Werte der Wahrscheinlichkeitsfunktion $P(M)$, und unten die Werte von $P(S|W,M)$ tabelliert.

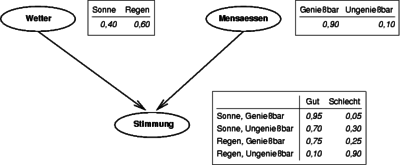
Im Beispiel bilden die drei Zufallsvariablen $W$ = Wetter, $M$ = Mensaessen und $S$ = Stimmung die Knoten eines bayesschen Netzes. Neben den Knoten für die Zufallsvariablen $W$ und $M$ sind tabellarisch deren unbedingte Wahrscheinlichkeitsverteilungen angegeben. Neben dem Knoten für die Zufallsvariable $S$ sind vier bedingte Wahrscheinlichkeitsverteilungen für die Zufallsvariable $S$, gegeben die vier möglichen Kombinationen von $W$ und $M$, angegeben. Die beiden Zufallsvariablen $W$ und $M$ sind die Eltern von $S$ und haben keine Eltern. Die beiden Pfeile (Kanten) werden kausal interpretiert.

Die gemeinsame Wahrscheinlichkeitsverteilung berechnet sich wegen der Stochastische Unabhängigkeit von M und W wie folgt:

$\operatorname {P} (S,W,M)=\operatorname {P} (S\mid W,M)\cdot \operatorname {P} (W)\cdot \operatorname {P} (M)$

Daher folgt die mit Hilfe des Gesetzes der totalen Wahrscheinlichkeit die Randverteilung

$\operatorname {P} (S)=\sum _{w\in E_{w}}\sum _{m\in E_{m}}\operatorname {P} (S\mid W=w,M=m)\cdot \operatorname {P} (W=w)\cdot \operatorname {P} (M=m)$

Mit den angegebenen Wahrscheinlichkeitsverteilungen lässt sich die Randverteilung von $S$ bestimmen. Beispielsweise gilt

${\begin{alignedat}{1}\operatorname {P} (S={\text{gut}})&=\ &\operatorname {P} (S={\text{gut}}\mid W={\text{Sonne}},M={\text{genießbar}})\cdot \operatorname {P} (W={\text{Sonne}})\cdot \operatorname {P} (M={\text{genießbar}})\\&&+\ \operatorname {P} (S={\text{gut}}\mid W={\text{Sonne}},M={\text{ungenießbar}})\cdot \operatorname {P} (W={\text{Sonne}})\cdot \operatorname {P} (M={\text{ungenießbar}})\\&&+\ \operatorname {P} (S={\text{gut}}\mid W={\text{Regen}},M={\text{genießbar}})\cdot \operatorname {P} (W={\text{Regen}})\cdot \operatorname {P} (M={\text{genießbar}})\\&&+\ \operatorname {P} (S={\text{gut}}\mid W={\text{Regen}},M={\text{ungenießbar}})\cdot \operatorname {P} (W={\text{Regen}})\cdot \operatorname {P} (M={\text{ungenießbar}})\\&=\ &0{,}95\cdot 0{,}40\cdot 0{,}90+0{,}70\cdot 0{,}40\cdot 0{,}10+0{,}75\cdot 0{,}60\cdot 0{,}90+0{,}10\cdot 0{,}60\cdot 0{,}10\;,\end{alignedat}}$

wobei alle benötigten Wahrscheinlichkeiten den drei Tabellen entnommen werden können.

Außerdem lässt sich über

$\operatorname {P} (S=s,W=w,M=m)=\operatorname {P} (S=s\mid W=w,M=m)\operatorname {P} (W=w,M=m)=\operatorname {P} (S=s\mid W=w,M=m)P(W=w)P(M=m)$

für $s\in \{{\text{gut}},{\text{schlecht}}\}$, $w\in \{{\text{Sonne}},{\text{Regen}}\}$ und $m\in \{{\text{genießbar}},{\text{ungenießbar}}\}$ die gemeinsame Wahrscheinlichkeitsverteilung von $S$, $W$ und $M$ bestimmen. Das erste Gleichheitszeichen ergibt sich aus der Definition einer bedingten Wahrscheinlichkeit und das zweite Gleichheitszeichen verwendet die stochastische Unabhängigkeit der Zufallsvariablen $W$ und $M$. Z. B. gilt

${\begin{aligned}\operatorname {P} (S={\text{gut}},W={\text{Sonne}},M={\text{genießbar}})&=\operatorname {P} (S={\text{gut}}\mid W={\text{Sonne}},M={\text{genießbar}})P(W={\text{Sonne}})P(M={\text{genießbar}})\\&=0{,}95\cdot 0{,}40\cdot 0{,}90\end{aligned}}$.

Analog lassen sich sieben weitere Wahrscheinlichkeiten für alle weiteren Kombinationen von Werten der Zufallsvariablen $S$, $W$ und $M$ berechnen.

Die gemeinsame Wahrscheinlichkeitsverteilung von $S$ und $W$ erhält man aus der gemeinsamen Wahrscheinlichkeitsverteilung von $S$, $W$ und $M$ als

$\operatorname {P} (S=s,W=w)=\operatorname {P} (S=s,W=w,M={\text{genießbar}})+\operatorname {P} (S=s,W=w,M={\text{ungenießbar}})$

für $s\in \{{\text{gut}},{\text{schlecht}}\}$ und $w\in \{{\text{Sonne}},{\text{Regen}}\}$.

Ist bekannt, dass die Stimmung gut ist, so lässt sich auf die Wahrscheinlichkeit sonnigen Wetters rückschließen:

${\begin{aligned}\operatorname {P} (W={\text{Sonne}}\mid S={\text{gut}})&={\frac {\operatorname {P} (S={\text{gut}},W={\text{Sonne}})}{\operatorname {P} (S={\text{gut}})}}\\&={\frac {\operatorname {P} (S={\text{gut}},W={\text{Sonne}})}{\operatorname {P} (S={\text{gut}},W={\text{Sonne}})+\operatorname {P} (S={\text{gut}},W={\text{Regen}})}}\;,\end{aligned}}$

wobei sich alle benötigten Wahrscheinlichkeiten aus der gemeinsamen Wahrscheinlichkeitsverteilung von $S$ und $W$ ergeben.

Schließen in bayesschen Netzen

Ist von manchen der Variablen, etwa E₁, ..., E_m, der Wert bekannt, d. h. es liegt Evidenz vor, so kann mit Hilfe verschiedener Algorithmen auch die bedingte Wahrscheinlichkeitsverteilung von X₁, ..., X_n mit gegebenen E₁, ..., E_m berechnet und damit Inferenz betrieben werden.

Das Inferenzproblem, sowohl das exakte wie auch das approximative, in Bayes’schen Netzen ist NP-schwer. In größeren Netzen bieten sich jedoch approximative Verfahren an. Exakte Verfahren sind zwar etwas genauer als approximative, dies spielt aber in der Praxis oft nur eine unwesentliche Rolle, da bayessche Netze zur Entscheidungsfindung eingesetzt werden, wo die genauen Wahrscheinlichkeiten nicht benötigt werden.

Zu beachten ist, dass bei Softwareumsetzungen exakter Inferenzverfahren oft nur doppelt genaue Gleitkommazahlen eingesetzt werden. Dadurch ist die Genauigkeit dieser Berechnungen eingeschränkt.

Exakte Inferenz

Zur exakten Inferenz in bayesschen Netzen eignen sich u. a. folgende Algorithmen:

• Variablenelimination
• Clustering-Algorithmen

Approximative Inferenz

• Rejection Sampling
• Likelihood weighting
• Self-Importance
• Adaptive Importance
• Markow-Ketten
• Monte-Carlo-Algorithmus, z. B. Gibbs-Sampling

Inferenztypen

• Diagnostisch: Von Effekten zu Ursachen
• Kausal: Von Ursachen zu Effekten
• Interkausal: Zwischen Ursachen eines gemeinsamen Effekts
• Gemischt: Kombination der Vorangegangenen

Lernen bayesscher Netze

Soll aus vorliegenden Daten automatisch ein bayessches Netz generiert werden, das die Daten möglichst gut beschreibt, so stellen sich zwei mögliche Probleme: Entweder ist die Graphenstruktur des Netzes bereits gegeben und man muss sich nicht mehr um die Ermittlung bedingter Unabhängigkeiten, sondern nur noch um die Berechnung der bedingten Wahrscheinlichkeitsverteilungen an den Knoten des Netzes kümmern, oder man muss neben den Parametern auch eine Struktur eines geeigneten Netzes lernen.

Parameterlernen

Geht man nicht von einem vollen (bayesschen) Wahrscheinlichkeitsmodell aus, wählt man im Allgemeinen

• Maximum-Likelihood-Schätzung (MLE)

als Schätzmethode. Für den Fall eines vollständigen (bayesschen) Wahrscheinlichkeitsmodells bietet sich zur Punktschätzung die

• Maximum-A-Posteriori-Schätzung (MAP)

an. Lokale Maxima der Likelihood- bzw. A-Posteriorifunktionen können im Fall von vollständigen Daten und vollständig beobachteten Variablen üblicherweise mit gängigen Optimierungsalgorithmen wie

• Gradientenverfahren oder
• Newton-Raphson-Verfahren

gefunden werden. Für den (als die Regel anzusehenden) Fall fehlender Beobachtungen wird üblicherweise der mächtige und weit verbreitete

• Expectation-Maximization-Algorithmus (EM), bzw. der
• Generalisierte Expectation-Maximization-Algorithmus (GEM)

verwendet.

Strukturlernen

Strukturlernen kann u. a. mit dem K2-Algorithmus (approximativ, unter Verwendung einer geeigneten Zielfunktion) oder dem PC-Algorithmus erfolgen.

Bedingte Unabhängigkeit

Zur Ermittlung bedingter Unabhängigkeiten zweier Variablenmengen gegeben eine dritte solche Menge genügt es, die Graphenstruktur des Netzes zu untersuchen. Man kann zeigen, dass der (graphentheoretische) Begriff der d-Separation mit dem Begriff der bedingten Unabhängigkeit zusammenfällt.

Anwendung

Bayessche Netze werden als Form probabilistischer Expertensysteme eingesetzt, wobei die Anwendungsgebiete unter anderem in Bioinformatik, Musteranalyse, Medizin und Ingenieurswissenschaften liegen. In der Tradition der Künstlichen Intelligenz liegt der Fokus bayesscher Netze auf der Ausnutzung derer graphischen Strukturen zur Ermöglichung abduktiver und deduktiver Schlüsse, die in einem unfaktorisierten Wahrscheinlichkeitsmodell undurchführbar wären. Realisiert wird dies durch die verschiedenen Inferenzalgorithmen.

Die Grundidee bayesscher Netze, nämlich die graphische Faktorisierung eines Wahrscheinlichkeitsmodells, wird auch in anderen Traditionen eingesetzt, wie in der Bayesschen Statistik und in der Tradition der sogenannten Graphischen Modelle zu Zwecken der Datenmodellierung. Anwendungsgebiete sind hier vor allem Epidemiologie, Medizin und Sozialwissenschaften.

Software

• GeNIe/SMILE
• bnlearn R package

Literatur

• Enrique Castillo, Jose Manuel Gutierrez, Ali S. Hadi: Expert Systems and Probabilistic Network Models. Springer-Verlag, New York 1997, ISBN 0-387-94858-9.
• Finn V. Jensen: Bayesian Networks and Decision Graphs. Springer-Verlag, New York 2001, ISBN 0-387-95259-4.
• Richard E. Neapolitan: Learning Bayesian Networks. Prentice Hall, 2003, ISBN 0-13-012534-2.
• Judea Pearl: Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. Morgan Kauffmann Publishers, San Francisco 1988, ISBN 0-934613-73-7.
• Judea Pearl: Causality. Cambridge University Press, Cambridge 2000, ISBN 0-521-77362-8.
• Stuart Russell, Peter Norvig: Künstliche Intelligenz – Ein moderner Ansatz. Pearson Education Deutschland, Deutschland 2004, ISBN 3-8273-7089-2.