Benutzer:Felix92/Übersetzungswerkstatt

Dieser Artikel ist im Entstehen und noch nicht Bestandteil der freien Enzyklopädie Wikipedia.

Solltest du über eine Suchmaschine darauf gestoVorlage:SSen sein, bedenke, dass der Text noch unvollständig sein und Fehler oder ungeprüfte Aussagen enthalten kann. Wenn du Fragen zum Thema hast, nimm Kontakt mit dem Autor Felix92 auf.

Camden
Ursprüngliches Kershaw County Court in Camden
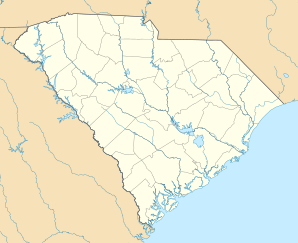
Lage in South Carolina
Camden
Basisdaten
Gründung:	22. März 1786
Staat:	Vereinigte Staaten
Bundesstaat:	South Carolina
County:	Kershaw County
Koordinaten:	34° 16′ N, 80° 37′ W34.259166666667-80.60916666666757
Zeitzone:	Eastern (UTC−5/−4)
Einwohner:	7.126 (Stand: 2016)
Fläche:	27,7 km² (ca. 11 mi²) davon 26,1 km² (ca. 10 mi²) Land
Bevölkerungsdichte:	273 Einwohner je km²
Höhe:	57 m
Postleitzahlen:	29020, 29021
Vorwahl:	+1 803
FIPS:	45-10855
GNIS-ID:	1247113
Bürgermeister:	Alfred Mae Drakeford

Camden ist ein Stadt im Kershaw County im Bundesstaat South Carolina in den Vereinigten Staaten. Sie ist die größte Stadt und fungiert als County Seat von Kershaw County.

Geographie

Camden liegt 47 km nördlich von Sumter, 48 km nordöstlich der Hauptstadt des Bundesstaates Columbia, 241 km nördlich von Charleston, 190 km westlich von Myrtle Beach und 137 km südöstlich von Charlotte. Es liegt nördlich der Interstate 20, an der Kreuzung von US 1 und US 521 und 601.

Geschichte

Camden ist die viert älteste Stadt South Carolinas. Es liegt in der Nähe des Zentrums des Cofitachequi-Stamms, das in den 1500er Jahren existierte. Im Jahre 1730 wurde Camden Teil eines von König Georg II. angeordneten Gemeindeplanes. Ursprünglich im Jahre 1732 als Fredericksburg im süden des heutigen Stadtgebiets angelegt. Jedoch wählten viele Siedler die höher liegende Stelle im Norden, wodurch die Siedlung Fredericksburg verschwand. Im Jahre 1758 kam Joseph Kershaw aus Yorkshire, England, in die Gemeinde und etablierte ein Geschäft und benannte die Gemeinde in Pine Tree Hill um. Camden wurde das wichtigste Binnenhandelszentrum in der Kolonie. Kershaw schlug vor, dass die Stadt in Camden umbenannt werden sollte, zu Ehren von Lord Camden, einem Vorkämpfer der Kolonialrechte im britischen Parlament.

Im August 1780 fand während des Amerikanischen Unabhängigkeitskriegs 10 km nördlich von Camden die Schlacht bei Camden statt. Es war eine der größten Niederlage der US-Amerikaner im Unabhängigkeitskrieg.

Demographie

Bevölkerungsentwicklung
Census	Einwohner		± rel.
1850	1133		—
1860	1621		43,1 %
1870	1007		−37,9 %
1880	1780		76,8 %
1890	3533		98,5 %
1900	2441		−30,9 %
1910	3569		46,2 %
1920	3930		10,1 %
1930	5183		31,9 %
1940	5747		10,9 %
1950	6986		21,6 %
1960	6842		−2,1 %
1970	8532		24,7 %
1980	7462		−12,5 %
1990	6696		−10,3 %
2000	6682		−0,2 %
2010	6838		2,3 %
Schätzung 2016	7126		4,2 %
U.S. Decennial Census

Bei der Volkszählung von 2010 gab es 6.838 Personen, die in den Stadtgrenzen wohnten, in 2.967 Haushalten und 1.800 Familien.

Es gab 2.967 Haushalte, indenen 27,7 % Kinder unter 18 Jahren lebten, 41,1 % waren verheiratete Paare, die zusammen lebten, 16,5 % hatten einen weiblichen Haushälter ohne Ehemann und 36,3 % waren Nichtfamilien. 35,6 % aller Haushalte bestanden aus Einzelpersonen und 18,9 % der Haushalte bestanden aus jemanden der allein wohnte und der 65 Jahre oder älter war. Die durchschnittliche Haushaltsgröße betrug 2,26 und die durchschnittliche Familiengröße betrug 2,94.

Bekannte Personen der Stadt

• Bernard Baruch, Finanzier, Börsenspekulant, Politikberater und Philanthrop.
• Charles Bennett, NFL Spieler
• Mary Chesnut, Autorin und eine der bekanntesten Zeitzeuginnen
• Larry Doby, Baseballspieler, Mitglied der Baseball Hall of Fame
• Bobby Engram, NFL Spieler
• Vonnie Holliday, NFL Spieler
• Thomas Austin, NFL Spieler
• Lorenzo James, Politiker
• Michael Kohn, Baseballspieler
• Kathleen Parker, Journalistin, Gewinnerin des Pulitzer Preises 2010
• John C. West, Gouverneur des Bundesstaates South Carolina 1971 bis 1975

Die Wasserstein-Metrik (auch Vaserstein-Metrik) ist eine Metrik zwischen Wahrscheinlichkeitsmaßen auf einem gegeben metrischen Raum.

Intuitiv, wenn jede Verteilung als ein Haufen von "Schmutz" angehäuft auf $M$ betrachtet wird, ist die Metrik die minimale "Kosten" der Umwandlung eines Haufens in den anderen. Wegen dieser Analogie ist diese Metrik in der Informatik als Earth Mover's Metrik bekannt.

Den Namen erhielt die Metrik 1970 von Roland Lwowitsch Dobruschin, der sie nach Leonid Vaseršteĭn benannte. Vaseršteĭn führte das Konzept 1969 ein.

Definition

Sei $(M,d)$ ein metrischer Raum, indem jedes Wahrscheinlichkeitsmaß ein Radonmaß auf $M$ ist, auch Radon-Raum genannt. Für $p\geq 1$ sei $P_{p}(M)$ die Menge aller Wahrscheinlichkeitsmaße $\mu$ auf $M$ mit endlichem p-ten Moment, das heißt für einige $x_{0}$ aus $M$ gilt:

$\int _{M}d(x,x_{0})^{p}\mathrm {d} \mu (x)<+\infty .$

Dann ist die p-te Wassersteindistanz zwischen zwei Wahrscheinlichkeitsmaß $\mu$ und $\nu$ in $P_{p}(M)$ definiert als:

$W_{p}(\mu ,\nu ):=\left(\inf _{\gamma \in \Gamma (\mu ,\nu )}\int _{M\times M}d(x,y)^{p}\mathrm {d} \gamma (x)\right)^{\frac {1}{p}},$

wobei $\Gamma (\mu ,\nu )$ die Menge aller Maße auf $M\times M$ bezeichnet, mit $\mu$ und $\nu$ als Randverteţilung bezüglich des ersten beziehungsweise zweiten Faktors. ($\Gamma (\mu ,\nu )$ wird auch die Menge aller Kopplungen zwischen $\mu$ und $\nu$ genannt.)

Beispiele

Dirac-Maß

Seien $\mu =\delta _{a_{1}}$ und $\nu =\delta _{a_{2}}$ zwei Dirac-Maße mit $a_{1},a_{2}\in \mathbb {R}$. Dsnn ist die einzige mögliche Kopplung $\delta _{(a_{1},a_{2})}$. Nimmt man nun als Distanzfunktion die Betragsfunktion auf $\mathbb {R}$, so erhält man für jedes beliebige $p\geq 1$:

$W_{p}(\mu ,\nu ):=|a_{1}-a_{2}|$

Ist nun $a_{1},a_{2}\in \mathbb {R} ^{n}$ und nimmt man statt der Betragsfunktion den euklidischen Abstand, so erhält man:

$W_{p}(\mu ,\nu ):=||a_{1}-a_{2}||_{2}$

Normalverteilung

Seien $\mu ={\mathcal {N}}(m_{1},C_{1})$ und $\nu ={\mathcal {N}}(m_{2},C_{2})$ zwei Normalverteilungen auf dem $\mathbb {R} ^{n}$, mit Erwartungswerten $m_{1},m_{2}\in \mathbb {R} ^{n}$ und Kovarianzmatrizen $C_{1},C_{2}\in \mathbb {R} ^{n\times n}$. Nimmt man nun als Distanzfunktion den euklidischen Abstand, so ist die 2-Wasserstein-Metrik zwischen $\mu$ und $\nu$:

$W_{2}(\mu ,\nu )^{2}:=||m_{1}-m_{2}||_{2}^{2}+\operatorname {Spur} \left(C_{1}+C_{2}-2(C_{1}^{1/2}C_{1}C_{2}^{1/2})^{1/2}\right)$.

Dieses Ergebnis verallgemeinert das vorangegangene Beispiel, mit $p=2$, da das Dirac-Maß als Normalverteilungen mit Kovarianzmatrix gleich null betrachtet werden kann. Dann entfällt der Spurterm und es bleibt der Abstand zwischen den Erwartungswerten.

Einzelnachweise

en:Wasserstein metric