Benutzer:Peter Buch/Cantor-Funktion

Die Cantor-Funktion ist in der Mathematik ein Beispiel für eine Funktion, die stetig, aber nicht absolut stetig ist. Sie wird auch als Cantorsche Treppenfunktion bezeichnet. Georg Cantor führte 1884 die Cantor-Funktion ein und erwähnte, dass Scheeffer sie als Gegenbeispiel zu einer von Harnack behaupteten Erweiterung des Fundamentalsatzes der Analysis anführt. Die Cantor-Funktion wurde durch Scheeffer, Lebesgue and Vitali untersucht und bekannt gemacht.
Definition
Vergleiche nebenstehende Abbildung. Zur formalen Definition der Cantor-Funktion c : [0,1] → [0,1] werde c(x) in folgenden Schritten bestimmt:
- Drücke x aus [0,1] zur Basis 3 aus.
- Falls x eine Ziffer "1" enthält, ersetze alle Ziffern hinter der ersten "1" durch "0".
- Ersetze alle Ziffern "2" durch "1".
- Lies das Ergebnis als Binärzahl. Das Ergebnis ist c(x).
Beispiele:
- 1/4 wird 0,02020202... zur Basis 3; da keine "1" enthalten ist, bleibt das im nächsten Schritt 0,02020202...; dies wird umgeschrieben in 0,01010101...; zur Basis 2 gelesen ist das 1/3, also ist c(1/4) = 1/3.
- 1/5 wird 0,01210121... zur Basis 3; die Ziffern hinter der ersten "1" werden durch "0" ersetzt, was 0,01000000... ergibt; dies wird nicht umgeschrieben, weil keine "2" vorkommt; zur Basis 2 gelesen ist das 1/4, also ist c(1/5) = 1/4.
- 200/243 wird 0,21102 (oder 0,211012222...) zur Basis 3; die Ziffern hinter der ersten "1" werden durch "0" ersetzt, was 0,21 ergibt; dies wird umgeschrieben in 0,11; zur Basis 2 gelesen ist das 3/4, also ist c(200/243) = 3/4.
Eigenschaften
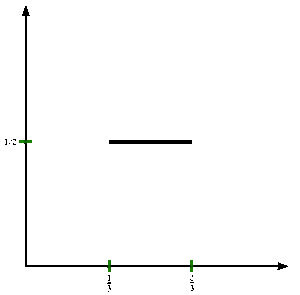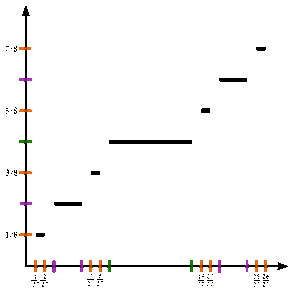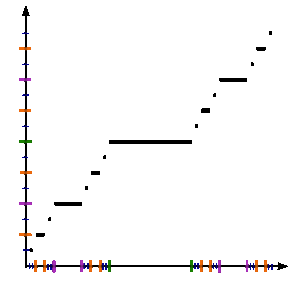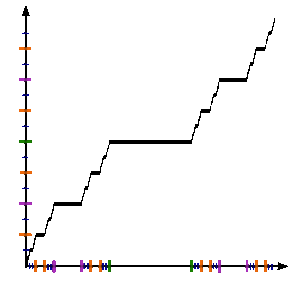
Die Cantor-Funktion widerspricht allzu intuitiven Vorstellungen von Stetigkeit und Maß; obwohl sie überall stetig ist und fast überall die Ableitung 0 hat, geht c, wenn x von 0 nach 1 geht, ebenfalls von 0 nach 1 und nimmt dabei jeden Zwischenwert an. Die Cantor-Funktion ist das meistzitierte Beispiel einer reellen Funktion, die gleichmäßig stetig (genauer Hölder-stetig zum Exponenten α = log2/log3), aber nicht absolut stetig ist. Sie ist konstant auf Intervallen der Form (0,x1x2x3...xn022222..., 0,x1x2x3...xn200000...), und jeder Punkt außerhalb der Cantor-Menge liegt in einem dieser Intervalle. Daher ist ihre Ableitung = 0 außerhalb der Cantor-Menge. Andererseits existiert keine Ableitung in einer überabzählbaren Teilmenge der Cantor-Menge, welche die Endpunkte der oben genannten Intervalle enthält. Nach links mit dem Wert 0 und nach rechts mit dem Wert 1 erweitert, ist sie die (kumulative) Verteilungsfunktion einer auf der Cantor-Menge gleichverteilten Zufallsvariablen. Diese so genannte Cantor-Distribution <?>hat keine diskreten Teile. Das heißt das entsprechende Maß ist atomfrei. Deshalb gibt es keine Sprung-Unstetigkeiten in der Funktion; jeder solcher Sprung würde einem Atom im Maß entsprechen</?>.
Jedoch kann kein nicht-konstanter Teil der Cantor-Funktion als Integral einer Wahrscheinlichkeitsdichtefunktion dargestellt werden; das Integral über eine beliebige Wahrscheinlichkeitsdichtefunktion, die über jedem Intervall nicht fast überall verschwindet, ergibt für manche Intervalle positive Werte, für die die Cantor-Distribution null ergibt.<?>integrating any putative probability density function that is not almost everywhere zero over any interval will give positive probability to some interval to which this distribution assigns probability zero.</?> Insbesondere hat Vitali gezeigt, dass die Funktion nicht das Integral ihrer Ableitung ist, obwohl die Ableitung fast überall existiert.
Die Cantor-Funktion ist das Standardbeispiel einer singulären Funktion.
Die Cantor-Funktion ist monoton steigend, und daher ist ihr Graph eine rektifizierbare Kurve. Die Bogenlänge des Graphs ist = 2 (Scheeffer 1884).
Alternative Definitionen
Iterative Konstruktion
Im Folgenden definieren wir eine Folge von Funktionen {ƒn} auf dem Einheitsintervall, die gegen die Cantor-Funktion konvergiert.
Sei ƒ0(x) = x.
Dann wird für jede ganze Zahl n ≥ 0 die nächste Funktion ƒn+1(x) mit Hilfe von ƒn(x) wie folgt definiert:
ƒn+1(x) = ƒn(3x)/2 für 0 ≤ x ≤ 1/3 ;
ƒn+1(x) = 1/2 für 1/3 ≤ x ≤ 2/3 ;
ƒn+1(x) = (ƒn(3 x−2)+1)/2 für 2/3 ≤ x ≤ 1 .
Die drei Definitionen an den Endpunkten 1/3 und 2/3 kompatibel, weil durch Induktion ƒn(0) = 0 und ƒn(1) = 1 für jedes n ist. Es lässt sich leicht zeigen, dass ƒn punktweise gegen die oben definierte Cantor-Funktion konvergiert. Darüber hinaus ist die Konvergenz gleichmäßig. Tatsächlich sieht man, getrennt für die drei Fälle der Definition von ƒn+1, dass
Wenn ƒ die Grenzfunktion bezeichnet, folgt für jedes n ≥ 0, dass
Auch kommt es nicht wirklich auf die Wahl der Startfunktion an, solange ƒ0(0) = 0, ƒ0(1) = 1, und ƒ0 beschränkt ist.
Fraktales Volumen
Die Cantor-Funktion ist eng mit der Cantor-Menge verwandt. Die Cantor-Menge C kann definiert werden als die Menge der Zahlen im Intervall [0, 1], die nicht die Ziffer "1" in ihrer Darstellung zur Basis 3 enthalten, außer wenn nach der "1" alle weiteren Ziffern "0" sind (dann könnte die Ziffernfolge 1000... durch 0222... ersetzt werden, um jegliche "1" zu vermeiden). Es zeigt sich, dass die Cantor-Menge ein Fraktal ist mit (überabzählbar) unendlich vielen Punkten (nulldimensionalem Volumen), aber mit der Länge null (eindimensionalem Volumen). Nur das D-dimensionale Volumen (im Sinne eines Hausdorff-Maßes) hat einen endlichen Wert, wobei die fraktale Dimension von C ist. Alternativ kann die Cantor-Funktion definiert werden als das D-dimensionale Volumen von Teilmengen der Cantor-Menge:
Verallgemeinerung
Sei
die duale (binäre) Darstellung der reellen Zahl 0 ≤ y ≤ 1 mit Hilfe binärer Ziffern bk = {0,1}. Damit bildet man die Funktion
Für z = 1/3 ist das Inverse der Funktion die Cantor-Funktion. Allgemein sieht Cz(y) für jedes z < 1/2 wie eine auf die Seite gedrehte Cantor-Funktion aus, wobei die Stufen weiter werden, wenn sich z der Null nähert.
References
- Richard Franklin Bass [2011]: Real analysis for graduate students, Second. Auflage, Createspace Independent Publishing, 2013, ISBN 978-1-4818-6914-0.
- Cantor, G. (1884), “De la puissance des ensembles parfaits de points”, in Acta Math., volume 4, DOI:, pages 381–392 Reprinted in: E. Zermelo (Ed.), Gezammelte Abhandlungen Mathematischen und Philosophischen Inhalts, Springer, New York, 1980.
- Darst, Richard B.; Palagallo, Judith A.; Price, Thomas E. (2010) Curious curves, World Scientific Publishing Co. Pte. Ltd., ISBN 978-981-4291-28-6
- Dovgoshey, O.; Martio, O.; Ryazanov, V.; Vuorinen, M. (2006), “The Cantor function”, in Expo. Math.[1], volume 24, issue 1, pages 1–37
- Fleron, J.F. (1994), “A note on the history of the Cantor set and Cantor function”, in Math. Mag., volume 67, JSTOR 2690689, pages 136–140
- Lebesgue, H. (1904) Leçons sur
l’intégration et la recherche des fonctions primitives, Gauthier-Villars
- Scheeffer, Ludwig (1884), “Allgemeine Untersuchungen ûber Rectification der Curven”, in Acta Math., volume 5, DOI:, pages 49–82
- Brian S. Thomson, Judith B. Bruckner, Andrew M. Bruckner [2001]: Elementary real analysis, Second. Auflage, ClassicalRealAnalysis.com, 2008, ISBN 978-1-4348-4367-8.
- Vitali, A. (1905), “Sulle funzioni integrali”, in Atti Accad. Sci. Torino Cl. Sci. Fis. Mat. Natur., volume 40, pages 1021-1034
External links
- Cantor ternary function at Encyclopaedia of Mathematics
- Cantor Function by Douglas Rivers, the Wolfram Demonstrations Project.
- Eric W. Weisstein: Cantor Function. In: MathWorld (englisch).
Category:Fractals Category:Measure theory Category:Special functions

![{\displaystyle \max _{x\in [0,1]}|f_{n+1}(x)-f_{n}(x)|\leq {\frac {1}{2}}\,\max _{x\in [0,1]}|f_{n}(x)-f_{n-1}(x)|,\quad n\geq 1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7acaa19c93f0ab49392691dfffce664ab89d1e14)
![{\displaystyle \max _{x\in [0,1]}|f(x)-f_{n}(x)|\leq 2^{-n+1}\,\max _{x\in [0,1]}|f_{1}(x)-f_{0}(x)|.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1b4bde40fc0cfc15e77ef2205a2ea62dd9a68eb)





