Bogen (Architektur)

Tragender Bogen über dem Portal, daneben unvollständige Blendbögen
Als Bogen bezeichnet man in der Architektur ein Bauelement zum Überbrücken von Öffnungen im Mauerwerk.[1] Ein Bogen ohne tragende Funktion heißt Blendbogen.
Form und Breite werden so gewählt, dass im Bogen keine Zugkräfte auftreten. Der Bogen deckt die sogenannte Stützlinie. Die in den Kämpfern an seinen Enden aufzubringenden Kräfte sind gegen die Vertikale geneigt, d. h., dass dort neben vertikalem Druck auch horizontaler Schub herrscht.
Das Gewölbe ist die Urform des Bogens. Später hinzugekommene Bögen bestehen aus Holz, Eisen oder Beton. Die Ausdehnung eines Bogens in die Dritte Dimension ist das Tonnengewölbe, ein um seine senkrechte Mittelachse gedrehter Bogen wird zur Kuppel.
Bögen sind bis zur Fertigstellung nicht selbsttragend und benötigen ein Lehrgerüst.
Sogenannte falsche Bögen oder Kragbogen bestehen aus sukzessive weiter zur Mitte reichenden Verlängerungen gerader Balken. Sie lassen sich ohne Lehrgerüst erstellen.
Der Bogen ist in der Architektur an zahlreichen Bauwerken in unterschiedlichen Ausführungen zu finden. So ermöglicht der Bogen Tür- und Fensteröffnungen ebenso wie das Überspannen von Hallen. Im Bauwesen wird er in Brücken und in Tunneldecken verwendet.
Echter und unechter Bogen
Kragbogen oder unechter Bogen

Vor der Erfindung des echten Bogens verwendete man Kragbögen. Damit konnten nur geringe Weiten überspannt werden. Die Stabilität wurde durch seitliche Auflasten erreicht.
Echter Bogen

Lockeres Mauerwerk besitzt überhaupt keine Zugfestigkeit. Auch Mörtel ändert daran wenig. Seine Aufgabe ist es, die Auflage der Steine zu verbessern, nicht aber, die Steine zu verkleben. Hingegen ist die Druckfestigkeit außerordentlich hoch. Bei Zement liegt sie bei ca. 50 MN/m², ca. 10-fach höher als die Zugfestigkeit.
Balken und Kragbogen setzen Materialien voraus, die unter Zug belastbar sind. Erst eine Bogenkonstruktion nutzt die hohe Druckbelastbarkeit von mineralischen (Stein und Beton) und keramischen (Ziegel) Baustoffen.
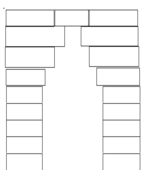
Die Steine in den beiden Bildern rechts sind keilförmig angeschrägt und lassen sich zu einem Bogen zusammenfügen. Nur die beiden „Pfosten“ sind gegen seitliches Verschieben gesichert. Die Bogensteine selber sind nicht verklebt und können daher keine Zugkräfte aufnehmen. Die auf diese Weise lose aneinanderliegenden Steine vermögen dennoch hohe Belastungen als Druckspannungen aufzunehmen, die – im Gegensatz zu einem Kragbogen – ein Vielfaches des Eigengewichts betragen.

1: Schlussstein, Scheitel[a]
2: Bogenstirn/Bogenhaupt (hier: an einem Keilstein)
3: Bogenrücken (hier: an einem Keilstein)
4: Kämpfer oder Widerlager
> der Stein darüber wird als Anfänger bezeichnet, seltener auch als Kämpferstein oder Gewölbefuß
> die Linie dazwischen (nicht eingezeichnet) wird als Kämpferlinie[b] bezeichnet
5: Bogenlaibung
6: Stichhöhe
7: Spannweite/Lichte Weite
8: Stützmauerwerk
a Scheitelhöhe (nicht eingezeichnet): Abstand des Scheitels vom Boden
b Kämpferhöhe (nicht eingezeichnet): Abstand der Kämpferlinie vom Boden
Die angeschrägten Bogensteine heißen Keilsteine. Der mittlere Stein im Bogen wird Schlussstein (S, siehe Bild rechts) genannt und ist häufig dekorativ herausgearbeitet.
Der Kämpfer (K) ist zugleich der obere Abschluss des Widerlagers und die Basis des Bogens. Dieser Übergangsbereich muss sorgfältig gearbeitet sein, damit die Druckkräfte des Bogens abgeleitet werden können. Die Steine oberhalb der Kämpferlinie (kl) liegen beim Errichten des Bogens nicht mehr durch ihr eigenes Gewicht auf dem Widerlager auf. Sie müssen beim Bau durch ein Lehrgerüst abgestützt werden, um nicht herabzufallen. Oberhalb der Kämpferlinie beginnt der eigentliche Bogen.
Die ersten Steine, die auf dem Kämpfer aufliegen, bezeichnet man als Anfänger (A). Die Bogenlaibung ist die Innenfläche des Bogens (in der Abbildung dunkelgrau schattiert), die Vorderfront die Bogenstirn. Die obere Fläche des Bogens, der Bogenrücken, trägt die nach oben aufgeschichteten Steine. Als Bogenscheitel bezeichnet man den höchsten Punkt der Bogenlaibung. Ein gestelzter Bogen steht mit seinen Enden auf mehr oder weniger hohen, oder mehreren senkrechten Anfängern, die auch als Bogenstelzung bezeichnet werden. In der Regel sind Bogenstelzungen symmetrisch angeordnet. Eher selten sind unsymmetrische oder einhüftige Stelzungen.
Ein sich nach unten öffnender Bogen, der die Kräfte gleichmäßig als Druckspannung aufnimmt, kann als Umkehrung einer frei hängenden Kette aufgefasst werden, in der ausschließlich Zugkräfte herrschen. Die Ideallinie eines unbelasteten Bogens ist deshalb eine Katenoide. Dennoch kommt ein Halbkreisbogen einer Brücke der Idealstruktur recht nahe, da der Bogen durch die seitlichen Brückenrampen am Anfang und Ende mehr Masse zu tragen hat als die Mitte.
Während sich die altgriechischen Stein-Monumentalbauten aus Tradition an Holzkonstruktionen orientierten, setzten die Römer durchgängig Halbrundbogen als tragende Strukturen ein (s. u.).
Bogenformen – Überblick
Im Laufe der Jahrhunderte wurden verschiedenste Arten von Bögen entwickelt, mit entsprechenden Vor- und Nachteilen.
Giebelbogen

Der Giebelbogen, auch Dreiecksbogen genannt (franz. Arc en mitre), ist eine Bogenkonstruktion aus zwei schräg, in Giebelform, aneinandergelegten Steinen oder Steinreihen. Er wird insofern von zwei Geraden gebildet, erfüllt aber konstruktiv die Voraussetzungen eines Bogens.[2]
Rundbogen oder Halbkreisbogen

Beim Kreisbogen, auch Rundbogen genannt, ist die Bogenlinie kreisförmig und nimmt den kompletten Halbkreis (180 Grad) ein, das bedeutet, die untersten beiden Fugen liegen horizontal. Die Höhe des Bogens (Scheitelhöhe) beträgt damit immer genau die halbe Spannweite. Der Halbkreisbogen war lange Zeit die dominierende Technik des Bogenbaus. Sie wurde von den Römern perfektioniert und vielfältig angewendet, was bis in die Zeit der Romanik wirkte.
→ für eine Konstruktionsanleitung des Bogens siehe weiter unten
Spitzbogen oder Gotischer Bogen

Der Spitzbogen ist ein aus zwei Kreisen konstruierter Bogen mit Spitze. Er gilt in der Architektur als ein zentrales Element der Gotik.[3]
Erste Spitzbögen fanden sich bereits in der Burgundischen Romanik. In der gotischen Sakralarchitektur (Basilika Saint-Denis) wurden sie seit der ersten Hälfte des 12. Jahrhunderts verwendet. Von Frankreich aus verbreitete sich diese Bogenform um 1200 nach Deutschland, wurde bis in das frühe 16. Jahrhundert hinein benutzt und Jahrhunderte später, in der Neugotik, wieder aufgegriffen.
Den gotischen Bogen gibt es auch als gedrückten Spitzbogen und als überhöhten Spitzbogen, letzterer heißt auch Lanzettbogen.
→ für Konstruktionsanleitungen verschiedener gotischer Bögen siehe weiter unten
Tudorbogen

Als Tudorbogen bezeichnet man in der Baukunst einen für den Tudorstil (die letzte Periode des gotischen Stils in England, 1485 bis 1603) charakteristischen sehr flachen Spitzbogen. Er fand vor allem in England Verbreitung, weshalb er auch englischer Spitzbogen oder normannischer Bogen genannt wird. Er besteht aus vier Kreisbogen mit je zwei verschieden großen Radien.[4]
→ für eine Konstruktionsanleitung des Bogens siehe weiter unten
Kielbogen
Ein Bogen, dessen Kante wie das Profil eines auf dem Rücken liegenden Schiffes mit Kiel aussieht, wird Kielbogen genannt. Andere Bezeichnungen dafür sind Eselsrücken – abgeleitet von der Rückenform eines Esels – und Sattelbogen, Schottischer Bogen oder Akkolade. Er hat seinen Ursprung in Indien, wo er bereits seit dem 3. Jahrhundert v. Chr. Verwendung fand. In Europa ist er erst ab dem 13./14. Jahrhundert in der Spätgotik in Gebrauch.
→ für eine Konstruktionsanleitung des Bogens siehe weiter unten
Vorhangbogen

Der Vorhangbogen ist ein Bogen, der von zwei oder mehr konvexen Bogenlinien begrenzt wird.[5] Im Fall von zwei Bogenlinien heißt er auch Einfacher Vorhangbogen oder Konkaver Spitzbogen.[6]
Zackenbogen
Der Zackenbogen ist eine Bogenform, dessen Laibung aus Pässen und Nasen besteht. Die einfachste Form eines Zackenbogens ist der Kleeblattbogen oder auch Dreipassbogen. Der Kleeblattbogen setzt sich aus drei Kreisbogen zusammen, wobei der mittlere Kreisbogen größer sein kann. Es gibt auch spitze Kleeblattbogen, bei denen der mittlere Bogen ein Spitzbogen ist.
Besteht ein Zackenbogen aus mehr als drei Bogen, so ist dies der eigentliche Zackenbogen, der auch Vielpassbogen oder Fächerbogen genannt wird.
Korbbogen

Der Korbbogen (auch: gedrückter Bogen, Korbhenkelbogen, Ratebogen) vereinigt Eigenschaften des Halbkreisbogens und des Segmentbogens; wie bei dem erstgenannten gehen die Senkrechten bruchlos in den Bogen über. Der Höhenbedarf wird dadurch vermindert, dass der Krümmungsradius von den Kämpfern zum Scheitel hin zunimmt, die Krümmung vom Scheitel zu den Widerlagern. Üblicherweise wurden solche Bögen aus Segmenten mit bestimmten Radien und Mittelpunkten konstruiert, der Radius kann aber auch kontinuierlich zu- und wieder abnehmen. Bogen mit drei oder fünf Mittelpunkten sind die Regel.[7]

Eine Sonderform des Korbbogens ist der einhüftige Korbbogen, auch Schwanenhals, steigender Bogen, fallender Bogen, strebender Bogen, geschwungener Bogen, Hornbogen, Spannbogen oder Hüftbogen genannt, bei dem die Kämpferpunkte in unterschiedlicher Höhe liegen. Dieser Bogentyp ist oft im Strebewerk gotischer Kirchen zu finden. Auch für die tragende Unterkonstruktion von Treppen wird der einhüftige Korbbogen verwendet.
→ für eine Konstruktionsanleitung des Bogens siehe weiter unten
Segmentbogen
Ein Segmentbogen (auch Flachbogen, Stichbogen, Kreisteilbogen, Teilzirkelbogen) ist ein Kreisbogen, der keinen vollen Halbkreis beschreibt, sondern ein Kreissegment mit einem Winkel kleiner 180°. Der Segmentbogen ist damit flacher als ein Halbkreisbogen. Nachteilig ist allerdings der größere Seitenschub, den der Segmentbogen ausübt. Die flache Bauweise mit Segmentbogen ist besonders vorteilhaft für weit gespannte Bogenbrücken, bei denen der Seitenschub in das angrenzende Erdreich eingeleitet wird und die damit deutlich flacher gebaut werden können als Brücken mit Halbkreisbogen.
→ für eine Konstruktionsanleitung des Bogens siehe weiter unten
Elliptischer Bogen

Formen: stehender-, steigender-, hochgestellter Ellipsenbogen. Der Bogenverlauf folgt der Ellipse. Beide Brennpunkte liegen auf der Kämpferlinie.[7]
Katenoide

Die Katenoide (Kettenlinie, Kettenkurve, Seilkurve) ist das mathematische Idealmodell eines Bogens mit gleichmäßiger Massenverteilung und ohne zusätzliche Krafteinwirkung. Freistehende Bögen dieser Form können sehr schlank ausgeführt werden. Ein Beispiel, jedoch mit ungleicher Massenverteilung, ist der Gateway Arch in St. Louis.
Parabelbogen

Aufgrund der geringen Abweichung von einer Katenoide werden Bögen manchmal auch als Parabel ausgeführt. Wenn der Bogen eine Last trägt, wie im Beispielbild links, flacht die Ideallinie ab. Sie ist dann weder eine Katenoide noch eine Parabel, sondern nähert sich einem Halbkreis an.
→ für eine Konstruktionsanleitung des Bogens siehe weiter unten
Hufeisenbogen
Hufeisenbogen haben ihren Namen von der hufeisenähnlichen Form. Die Bogenlänge beträgt zwischen 2/3 und 3/4 eines Kreisumfanges. Dieser Bogen ist in der islamischen Architektur vorherrschend und wird deshalb auch maurischer Bogen oder arabischer Bogen genannt. Allerdings verwendeten die Westgoten bereits den Hufeisenbogen in ihren Kirchenbauten (frühestes Beispiel: San Juan de Baños, geweiht 661, also bevor der Islam auf der iberischen Halbinsel Einzug hielt). Er kann als Rundbogen oder Spitzbogen ausgeführt sein.
Eine andere Spur führt nach Indien, wo die buddhistischen Chaitya-Fenster der Zeit um Christi Geburt und später die von ihnen abgeleiteten kudus und chandrasalas in Hufeisenform gestaltet sind (siehe auch die Schlüssellochfenster von Nachna). Der Hufeisenbogen fand in jüngerer Zeit auch im Jugendstil Verwendung.
→ für eine Konstruktionsanleitung des Bogens siehe weiter unten
Karniesbogen
Beim Karniesbogen setzen über der Kämpferlinie zwei Kragsteine mit konvex geschwungenem Profil an, an die sich der konkav geschwungene Bogen anschließt, so dass in der Verbindung der beiden Elemente eine S-förmige Linie entsteht. Karnies bezeichnet allgemein ein S-förmiges, also konkav-konvex profiliertes Bauelement.[8]
→ für eine Konstruktionsanleitung des Bogens siehe weiter unten
Schulterbogen

Der Schulterbogen ist eigentlich ein Scheitrechter Bogen, dessen Sturzstützweite durch darunterliegende Kragsteine oder auch Konsolsteine verkürzt wurde. Andere Bezeichnungen sind daher Konsolbogen und Kragsturzbogen, auch die Bezeichnungen Bursabogen findet man.[6]
Scheitrechter Bogen

Ein Scheitrechter Bogen, auch Horizontalbogen genannt, ist ein Bogen, der so ausgeführt ist, dass die Unterseite der überspannten Öffnung einem Türsturz gleicht. Konstruktiv ist es ein Segmentbogen, dessen Keilsteine so zugearbeitet werden, dass sich eine waagerechte Unterkante ergibt. Scheitrechte Bogen erlauben keine großen Spannweiten. Man findet sie häufig über Fenstern und Türen. Scheitrechte Bogen dienen auch als Entlastungsbogen über einem Fenstersturz aus Werkstein. Heute findet man viele unechte scheitrechte Bögen an neuen Bauwerken, die aber keine tragenden Bogenkonstruktionen sind, sondern in dahinterliegenden Stahlbetonstützen verankert sind. Oft sind sie leicht zu erkennen, weil die Steine nicht radial angeordnet sind oder weil der mittlere Schlussstein keine schrägen Seitenkanten aufweist oder gar verkehrt herum eingebaut wurde.
Scheitrechte Bogen werden im Feuerungsbau eingesetzt, um die Größe der Öffnungen etwas zu minimieren.
Gestelzter Bogen
Der Gestelzte Rund- oder Spitzbogen hat an beiden Bogenschenkeln über der Kämpferlinie einen geraden Anlauf.[9] Die Rundbogenvariante ist häufig in romanischen Chorapsiden zu finden, bei den den Chor umschließenden Arkaden, die sich in den Chorumgang öffnen.
Einsatz von Bögen

Bögen bei Gewölben
- Gurtbogen: Stützt Tonnengewölbe oder trennt einzelne Felder eines Kreuzgewölbes ab und verbindet die tragenden Pfeiler.
- Schildbogen
- Scheidbogen
- Chorbogen: ist ein Bogen zwischen Chor und Langhaus oder zwischen Chor und Vierung. Dieser Bogen wird auch Triumphbogen genannt.
Arkaden
Arkaden in der Alten Münze, München
Arkaden vor dem Schrein der Fatima Masuma
Mauerbogen, Fenster-, Tür- oder Torbogen
Ein Mauerbogen überspannt als Fensterbogen, Türbogen oder Torbogen eine Öffnung im Mauerwerk und trägt die Last des darüberliegenden Mauerwerks (siehe auch Archivolte)
Fensterbögen in Armenien
Torbogen, Culzean Castle
Torbogen auf den Philippinen
Entlastungs- oder Überfangbogen
Ein Entlastungs- oder Überfangbogen ist ein Bogen, der komplett im Mauerwerk liegt, um darunter liegende Teile zu entlasten und die Kräfte auf andere Bereiche zu verteilen. Sehr häufig über Fenster- und Türstürzen aus Werkstein gemauert. Der verbleibende Zwischenraum zwischen Sturz und Entlastungsbogen ist nur lose vermauert. Manchmal werden diese Bögen auch sichtbar zur Fassaden- oder Wandgliederung verwendet. Im Historismus kann er auch aus Sandstein bestehen oder sogar nur aufgeputzt sein, teilweise wird er durch einen Schlussstein verziert. Auch kleine, statisch unwirksame, über einer Wandöffnung vorgeblendete Bögen (meist stabförmig verziert) werden manchmal als Überfangbögen bezeichnet.[10]
Entlastungsbogen im Lexikon der gesamten Technik
Falscher Entlastungsbogen, Löwentor (Mykene)
Schwibbogen
Der Schwibbogen oder Schwiebbogen ist ein Bogen, der zwei Gebäude spreizt.[11] Der Bogen ist so übermauert, dass sich oben ein gerader Abschluss ergibt. Häufig findet sich der Schwibbogen in den engen Gassen mittelalterlicher Städte, z. B. Regensburgs.
Schwibbögen in der Via Botteghelle in Salerno
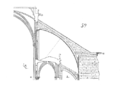
Strebebogen
Beim Strebebogen handelt es sich um einen asymmetrischen Bogen, der hoch aufragende Bauteile stützt. Er ist ein typisches Konstruktionsmerkmal an gotischen Basiliken als Teil des Strebewerkes.
Strebebogen an Notre Dame in Paris
Strebebogen am Straßburger Münster
Triumphbogen
Der Triumphbogen ist ein monumentales Denkmal, das in Form eines freistehenden Bogens errichtet wird. Auch der Chorbogen wird Triumphbogen genannt.
Triumphbogen in Maladsetschna, Belarus
Brückenbogen
Ein Brückenbogen ist tragendes Element einer Brücke aus Stein, ist Grenzfall zu einem Tonnengewölbe.
Bogenformen – geometrische Konstruktion
Folgende geometrische Konstruktionen werden für Bögen in der Praxis verwendet:[12]
Rundbogen oder Halbkreisbogen
Die Kämpferlinie AB halbiert, ergibt den Punkt M, den Einsatzpunkt für das Zeichnen des Rundbogens mit R=Strecke AM bzw. BM.
Spitzbogen oder Gotischer Bogen
Mit der Spannweite um Punkt A und um Punkt B einen Kreisbogen mit Radius R=AB schlagen, ergibt den Scheitelpunkt S. Die Verbindung der Punkte A, B, S ergeben ein gleichseitiges Dreieck.
Spitzbogen oder Gotischer Bogen, gedrückt
Auf der Kämpferlinie AB die Mittelsenkrechte errichten. Hierauf die Stichhöhe des Bogens abtragen, ergibt den Scheitelpunkt S. Die Stichhöhe muss wesentlich kleiner als die Spannweite, aber größer als die halbe Spannweite sein. Die Mittelsenkrechte auf der Strecke BS schneidet die Kämpferlinie und ergibt den Einsatzpunkt M1 zum zeichnen des Bogens mit R1. Durch Übertragen erhält man auf der anderen Seite den Einsatzpunkt M2.
Spitzbogen oder Gotischer Bogen, überhöht
(Konstruktion A) Die Einstichpunkte liegen bei dieser Konstruktion außerhalb der Kämpferpunkte und der Spannweite. Die Kämpferlinie wird in vier gleiche Teile geteilt. Die Strecke von 1/4 wird rechts und links der Kämpferpunkte angetragen und bilden die Einstichpunkte M1 und M2.
Tudorbogen
(Konstruktion A) Gegeben sind die Strecke AB und das Mittellot. Schlage um M einen Halbkreis, mit dem Radius AM, nach unten. Teile die Strecke AB in vier gleiche Teile. Es entstehen Punkt 1 und Punkt 2. Schlage um 1, mit dem Radius der Strecke zwischen 1 und 2, einen Bogen nach unten, der den Kreisbogen mit dem Radius AM schneidet. Der Schnittpunkt ist Punkt 3. Dieselben Konstruktionsschritte werden sinngemäß für Punkt 2 wiederholt und ergeben so Punkt 4. Zeichne nun Strahlen von Punkt 1 durch Punkt 3, und von Punkt 2 durch Punkt 4, zur Unterteilung der verschiedenen Kreisbögen. Die Punkte 1,2,3, und 4, sind die Einstichpunkte für den Tudorbogen.[13][14]
Kielbogen
Kielbogen (Konstruktion A). Gegeben sind die Strecke AB und das Mittellot. Die Strecke AB wird bei dieser Konstruktion in vier gleiche Teile (a) geteilt. Es entstehen die Punkte M1 und M2. Schlage um M1 und M2 jeweils einen Halbkreis. Es werden Senkrechte von Punkt M1 und M2 nach oben gezeichnet. Von den jeweiligen Scheitelpunkten der Halbkreise um M1 und M2 wird die Strecke a senkrecht nach oben abgetragen – es entstehen jetzt die Punkte M3 und M4. Um die Punkte M3 und M4 werden die Viertelkreise geschlagen. Es entsteht der Scheitelpunkt C.[15]
Korbbogen
Korbbogen aus drei Mittelpunkten
Zu der Spannweite S = AB zeichnet man zunächst die Mittelsenkrechte und trägt auf dieser die Stichhöhe H = MC ab. Dann verbindet man die Punkte A und C, trägt die Stichhöhe MC von M aus auf der Strecke AM ab und erhält Punkt D und somit die Strecke AD = L. Von C aus trägt man L auf der Strecke AC ab. Mittig zwischen A und dem Schnittpunkt E von L mit AC errichtet man eine Senkrechte auf AC und erhält am Schnittpunkt dieser Linie mit AB den Bogenmittelpunkt M1. Am Schnittpunkt dieser Senkrechten auf AC mit der Mittelsenkrechten aus dem ersten Schritt erhält man M2. Von M aus trägt man die Strecke MM1 auf der Strecke MB ab und erhält M3. Die Kreisbögen um die Bogenmittelpunkte M1, M2 und M3 ergeben den Korbbogen.[16][17]
Korbbogen aus fünf Mittelpunkten (näherungsweise)
Zunächst zeichnet man zu der Spannweite S = AB die Mittelsenkrechte, trägt auf dieser die Stichhöhe H = MC ab und an die Mittelsenkrechte in Punkt C einen Winkel von 45° an und erhält die Strecke DE = L. Von M aus trägt man nach rechts und links auf der Strecke AB die Strecke L ab und bekommt die Bogenmittelpunkte M1 und M2. Dann trägt man auf der Mittelsenkrechten von M aus zweimal die Strecke L nach unten ab und erhält den Punkt F und den Bogenmittelpunkt M3. Von Punkt F aus zeichnet man Linien durch die Bogenmittelpunkte M1 und M2, trägt an die Mittelsenkrechte in Punkt M nach links und rechts unten mit dem Winkel von 45° (Näherungswinkel – rechnerisch nicht genau!) und erhält die Bogenmittelpunkte M4 und M5. Linien vom Bogenmittelpunkt M3 durch die Bogenmittelpunkte M4 und M5 begrenzen den mittleren Bogenabschnitt. Die Kreisbögen um die Bogenmittelpunkte M1 – M5 ergeben den Korbbogen.[18] Der rechnerisch exakte Winkel beträgt 41,53° mit der Formel: .[17]
Korbbogen aus fünf Mittelpunkten (exakt)
Zunächst zeichnet man zu der Spannweite S = AB die Mittelsenkrechte und erhält den Schnittpunkt M, trägt auf der Mittelsenkrechten von M nach oben die Stichhöhe H = MC ab und im so erhaltenen Punkt C nach unten eine Linie mit einem Winkel von 45° zur Mittelsenkrechten an und erhält die Strecke DE = L. Auf der Strecke AB trägt man von M aus nach rechts und links die Strecke L ab und erhält die Bogenmittelpunkte M1 und M2. Dann trägt man auf der Mittelsenkrechten von M aus nach unten einmal die Strecke L ab und erhält den Punkt F. Von Punkt F aus zeichnet man Linien durch die Bogenmittelpunkte M1 und M2 und erhält FM1 bzw. FM2 = Y. Vom Punkt M trägt man nach links und rechts unten Linien mit dem Winkel von 45° zur Mittelsenkrechten an und erhält die Bogenmittelpunkte M3 und M4 (entspricht der Halbierung der Strecken Y von F zu den Bogenmittelpunkten M1 bzw. M2). Nun verbindet man die beiden Punkte M3 und M4 und erhält exakt L/2 unterhalb von M am Schnittpunkt dieser Verbindungslinie mit der Mittelsenkrechten den Punkt G. Von G aus trägt man auf der Mittelsenkrechten die Strecke Y (Strecke von F zu M1 bzw. F zu M2) nach unten ab und erhält den letzten Bogenmittelpunkt M5. Die Kreisbögen um die Bogenmittelpunkte M1 – M5 ergeben den Korbbogen. Die Punkte A und B sowie Linien durch M1 und M3 bzw. M2 und M4 begrenzen die beiden äußeren Bogenabschnitte. Linien durch M1 und M3 sowie M5 und M3 bzw. M2 und M4 sowie M5 und M4 begrenzen die beiden zwischen-Bogenabschnitte. Linien vom Bogenmittelpunkt M5 durch die Bogenmittelpunkte M3 sowie M4 begrenzen den zentralen Bogenabschnitt.[19]
Korbbogen aus elf Mittelpunkten
Bei mehr als drei Mittelpunkten kann die Form der Ellipse angenähert eingehalten werden, indem mit der halben Spannweite AO, der Pfeilhöhe OC sowie der Summe beider die Hilfskreise I I, II II und III III gezogen werden. Teilt man dann einen dieser Hilfkreise in eine gerade Anzahl n+1 gleicher Teile, wenn n die Anzahl der gewünschten Mittelpunkte bedeutet, zieht die Halbmesser O a2, O b2 u.s.w., bestimmt durch Ziehen der Parallelen a a', b b', u.s.w. zur großen Achse beziehungsweise zur kleinen Achse a1 a', b1 b', u.s.w. die Ellipsenpunkte a', b', c', u.s.w., so ergibt der Schnittpunkt der Verbindungslinie a2 a' mit AO den Mittelpunkt M11 für das erste Kreisstück A a'. Die Verbindungslinie b2 b' schneidet die Verlängerung des vorhergehenden Halbmessers im Mittelpunkt M10 u.s.w. Diese Ausführungsweise sowie die anderen verschiedenen graphischen Konstruktionen ergeben jedoch sehr schleifende Schnitte zur Bestimmung der Mittelpunkte, und es ist besser, die Halbmesser selbst oder die Koordinaten der Mittelpunkte durch Aufstellung entsprechender Gleichungen zu berechnen.[20][21]
Einhüftiger Korbbogen, Schwanenhals, steigender Bogen oder Hüftbogen
(Konstruktion A) Es wird bei gegebener Steigung EB im Mittelpunkt O der Spannweite AE eine Lotrechte errichtet. Strecke AD = DC. Dann wird von C eine Senkrechte auf AB gefällt. Es ergeben sich die Schnittpunkte M1 bzw. M2 mit AE bzw. mit der Waagerechten durch B. Die gesuchten beiden Mittelpunkte für die Kreisbögen sind gefunden.[22][23][24]
Segmentbogen, Flachbogen, Stichbogen
Auf der Kämpferlinie AB die Mittelsenkrechte errichten. Hierauf die Stichhöhe abtragen, ergibt den Scheitelpunkt S. Die Punkte A und B mit S verbinden. Die Mittelsenkrechten auf den Strecken AS und BS errichten. Sie schneiden sich im Punkt M. Punkt M ist der Einsatzpunkt zum Zeichnen des Stichbogens.
Gegeben sind Bogenachse AB und Stichhöhe C. Mittelsenkrechte der Strecke AC errichten; Schnittpunkt in M entsteht. Der Punkt M ist der gesuchte Kreismittelpunkt. Kreis mit dem Radius r=MC um M zeichnen. Der Kreisbogen zwischen den Kämpferpunkten A und B ist der gesuchte Segmentbogen.
Parabelbogen
Parabelbogenkonstruktion über Tangenten. Die Spannweite S und die Bogenhöhe MC sind bekannt. Die Strecke L= 1/1 wird in vier gleiche Teile aufgeteilt (L= 1/4). Nun werden Strecken a-a, b-b und c-c gebildet; es entstehen die Tangentenpunkte T1, T2, T3 für die Zeichnung einer Parabel.
Hufeisenbogen
Hufeisenrundbogen. Er besteht aus einem Rundbogen, dessen Mittelpunkt über der Kämpferebene liegt; er kann mit der halben Spannweite als Radius konstruiert werden. Der Hufeisenrundbogen wird mit einer Schrägen von 30° ab den Kämpferpunkten A und B konstruiert. Der Hufeisenspitzbogen wird mit einer Schrägen von 45° ab den Kämpferpunkten A und B konstruiert.
Karniesbogen
Es werden bei gegebener Stichhöhe C die Punkte A und C miteinander verbunden. Strecke AC wird in vier gleiche Abschnitte a geteilt. Es werden Lotrechte auf der Strecke AC nach oben zu der senkrechten A-Achse und nach unten zu der senkrechten C-Achse gezeichnet. Man erhält somit die Kreisbogen-Punkte M1 und M2. Es werden die Bögen miteinander verbunden und nach B gespiegelt.
Literatur
- Oscar Mothes: Illustriertes Bau-Lexikon Band 3, Leipzig, Spamer, 1868, 562 S. Online-Version, abgerufen am 4. Mai 2017.
- Glossarium Artis. Bd. 3. Bogen und Arkaden / Tübingen 1973; Rudolf E. Huber, Renate Rieth, Courvoisier, Jean; K.G. Saur Verlag KG, ISBN 3-598-10454-5
- Die Steinkonstruktionen. Franz Stade, Reprint-Verlag-Leipzig; Reprintauflage der Originalausgabe von 1907; Volker Hennig, Holzminden; ISBN 3-8262-1922-8
- Baufachkunde Hochbau. Verfasser Kohl, Bastian, Neizel. Teubner Stuttgart, Leipzig 1998. ISBN 978-3-322-83011-1, e-ISBN 978-3-322-83010-4.
- Karl-Eugen Kurrer: Geschichte der Baustatik. Auf der Suche nach dem Gleichgewicht, Kapitel 4 „Vom Gewölbe zum Bogen“, Ernst und Sohn, Berlin 2016, S. 198–273, ISBN 978-3-433-03134-6.
- S. Huerta, Karl-Eugen Kurrer: Zur baustatischen Analyse gewölbter Steinkonstruktionen, in: Mauerwerk-Kalender 2008, hrsgn. von W. Jäger, S. 373–422. Berlin: Ernst & Sohn 2008.
Weblinks
Einzelnachweise
- ↑ Definition Bogen. In: Meyers Großes Konversations-Lexikon. 6. Auflage. Band 3, Bibliographisches Institut, Leipzig/Wien 1905, S. 137–138.
- ↑ Absatz nach Hans Koepf, Günther Binding: Bildwörterbuch der Architektur (= Kröners Taschenausgabe. Bd. 194). 4., überarbeitete Auflage. Kröner, Stuttgart 2005, ISBN 3-520-19404-X. Die Synonymie zu Dreiecksbogen findet sich in der 4. Auflage nicht mehr, allerdings in der älteren 2. Auflage, ISBN 3-520-19402-3. In anderer Bedeutung wird unter Giebelbogen auch ein Ornament verstanden, so bei Günther Wasmuth (Hrsg.): Wasmuths Lexikon der Baukunst. Band 3: H bis Ozo. Wasmuth, Berlin 1931, vgl. Giebel#Giebelschmuck
- ↑ Spitzbogen. (PDF) Abgerufen am 19. Juli 2020.
- ↑ Tudorbogen auf Wissen.de
- ↑ Hans Koepf, Günther Binding: Bildwörterbuch der Architektur (= Kröners Taschenausgabe. Bd. 194). Kröner, Stuttgart 1999, ISBN 3-520-19403-1.
- ↑ a b Kleines Wörterbuch der Architektur, Reclam, Stuttgart, 1995.
- ↑ a b Wilhelm Friedrich: Tabellenbuch für das Bau- und Holzgewerbe. Ausgabe B. Fachbuchverlag GmbH., Leipzig 1951.
- ↑ Wilfried Koch: Baustilkunde. Das Standardwerk zur europäischen Baukunst von der Antike bis zur Gegenwart. 29., durchgesehene Auflage. Wissenmedia, Gütersloh u. a. 2009, ISBN 978-3-577-10231-5, S. 458.
- ↑ Nikolaus Pevsner, Hugh Honour, John Fleming: Lexikon der Weltarchitektur. 3., aktualisierte und erweiterte Auflage. Prestel, München 1992, ISBN 3-7913-2095-5.
- ↑ Überfangbogen – Wörterbuch
- ↑ Schwibbogen. Abgerufen am 4. Mai 2017.
- ↑ Harald Lotter und Alexander Wendel: Bogenarten. (Nicht mehr online verfügbar.) Archiviert vom Original am 28. November 2004; abgerufen am 9. Dezember 2013.
- ↑ Meyers Großes Konversations-Lexikon, 6. Auflage 1905–1909: Tudorbogen. Abgerufen am 8. Februar 2017.
- ↑ Tudorbogen. In: Luegers Lexikon der gesamten Technik. 2. Auflage. Band 8, Deutsche Verlags-Anstalt, Leipzig/Stuttgart 1910, S. 641.
- ↑ Kielbogen / Eselsrücken / geschweifter Spitzbogen. Abgerufen am 3. November 2017.
- ↑ Grundwissen Bau, Autoren: Batran, Frey, Hühn, Köhler, Kraus, Rothacher, Sonntag, Verlag: Handwerk und Technik GmbH, Hamburg 1985, ISBN 3-582-03500-X
- ↑ a b Rechenformeln für Korbbögen. Abgerufen am 23. April 2020.
- ↑ Bauzeichnen, Autoren: Dahmlos und Witte, 6. Aufl., Verlag: Gebrüder Jänecke, Hannover 1972, ISBN 3-7792-1032-0
- ↑ Korbbogen aus fünf Mittelpunkten. Abgerufen am 3. März 2021.
- ↑ Korbbogen. In: Luegers Lexikon der gesamten Technik. 2. Auflage. Band 5, Deutsche Verlags-Anstalt, Leipzig/Stuttgart 1907, S. 632–633.
- ↑ Rechenformeln für Korbbögen. Abgerufen am 7. Juni 2020.
- ↑ Die Konstruktionen in Stein. Verfasser G.A. Breymann. J.M. Gebhardt´s Verlag Leipzig, 1903, ISBN 3-88746-013-8.
- ↑ Einhüftige Korbbogenkonstruktionen. In: Luegers Lexikon der gesamten Technik. 2. Auflage. Band 5, Deutsche Verlags-Anstalt, Leipzig/Stuttgart 1907, S. 632–633.
- ↑ Rechenformeln für Korbbögen. Abgerufen am 23. April 2020.