Diffie-Hellman-Schlüsselaustausch

Der Diffie-Hellman-Schlüsselaustausch oder Diffie-Hellman-Merkle-Schlüsselaustausch bzw. -Schlüsselvereinbarung (auch kurz DHM-Schlüsselaustausch oder DHM-Protokoll[1]) ist ein Protokoll zur Schlüsselvereinbarung. Es ermöglicht, dass zwei Kommunikationspartner über eine öffentliche, abhörbare Leitung einen gemeinsamen geheimen Schlüssel in Form einer Zahl vereinbaren können, den nur diese kennen und ein potenzieller Lauscher nicht berechnen kann. Der dadurch vereinbarte Schlüssel kann anschließend für ein symmetrisches Kryptosystem verwendet werden (beispielsweise Data Encryption Standard oder Advanced Encryption Standard). Unterschiedliche Varianten des Diffie-Hellman-Merkle-Verfahrens werden heute für die Schlüsselverteilung in den Kommunikations- und Sicherheitsprotokollen des Internets eingesetzt, beispielsweise in den Bereichen des elektronischen Handels. Dieses Prinzip hat damit eine wichtige praktische Bedeutung.
Das Verfahren wurde von Whitfield Diffie und Martin Hellman entwickelt und im Jahr 1976 unter der Bezeichnung ax1x2 veröffentlicht. Es handelt sich um das erste der sogenannten asymmetrischen Kryptoverfahren (auch Public-Key-Kryptoverfahren), das veröffentlicht wurde. Wichtige Vorarbeiten leistete Ralph Merkle mit dem nach ihm benannten Merkles Puzzle. Wie erst 1997 bekannt wurde, entwickelten bereits in den frühen 1970er-Jahren Mitarbeiter des britischen Government Communications Headquarters (GCHQ) als Erste asymmetrische Kryptosysteme. Das GCHQ hat allerdings wegen der Geheimhaltung und wegen des für die Briten aus Sicht der frühen 1970er Jahre fraglichen Nutzens nie ein Patent beantragt.
Der DHM-Schlüsselaustausch zählt zu den Krypto-Systemen auf Basis des diskreten Logarithmus (kurz: DL-Verfahren). Diese basieren darauf, dass die diskrete Exponentialfunktion in gewissen zyklischen Gruppen eine Einwegfunktion ist. So ist in der primen Restklassengruppe die diskrete Exponentialfunktion , prim, auch für große Exponenten effizient berechenbar, deren Umkehrung, der diskrete Logarithmus, jedoch nicht. Es existiert bis heute kein „schneller“ Algorithmus zur Berechnung des Exponenten , bei gegebener Basis , Modul und gewünschtem Ergebnis.
Damit prägten die Forscher mit dem Verfahren auch einen neuen Sicherheitsbegriff in der Kryptographie, der darauf basiert, dass kein effizienter Algorithmus für die Kryptoanalyse existiert: Ein Kommunikationsprotokoll ist sicher, wenn dessen Kryptoanalyse so viel Zeit und Arbeit bedeutet, dass diese in der Praxis nicht ausgeführt werden kann. Das Problem, aus den beiden Nachrichten der Kommunikationspartner den geheimen Schlüssel zu berechnen, wird als Diffie-Hellman-Problem bezeichnet.
Der DHM-Schlüsselaustausch ist allerdings nicht mehr sicher, wenn sich ein Angreifer zwischen die beiden Kommunikationspartner schaltet und Nachrichten verändern kann. Diese Lücke schließen Protokolle wie das Station-to-Station-Protokoll (STS), indem sie zusätzlich digitale Signaturen und Message Authentication Codes verwenden.
Die Implementierung mittels elliptischer Kurven ist als Elliptic Curve Diffie-Hellman (ECDH) bekannt. Dabei werden die beim Originalverfahren eingesetzten Operationen (Multiplikation und Exponentiation) auf dem endlichen Körper ersetzt durch Punktaddition und Skalarmultiplikation auf elliptischen Kurven. Das -fache Addieren eines Punktes zu sich selbst (also die Multiplikation mit dem Skalar ) wird mit bezeichnet und entspricht einer Exponentiation im ursprünglichen Verfahren. Das Prinzip wurde Mitte der 1980er Jahre von Victor S. Miller und Neal Koblitz unabhängig voneinander vorgeschlagen.
Geschichte und Bedeutung
Öffentliche Kryptologie
Beim Diffie-Hellman-Merkle-Schlüsselaustausch handelt es sich um das erste der sogenannten asymmetrischen Kryptoverfahren (auch Public-Key-Kryptoverfahren), das veröffentlicht wurde. Es löst das Schlüsseltauschproblem, indem es ermöglicht, geheime Schlüssel über nicht-geheime, also öffentliche, Kanäle zu vereinbaren.
Den ersten Schritt zur Entwicklung asymmetrischer Verfahren machte Ralph Merkle 1974 mit dem nach ihm benannten Merkles Puzzle, das aber erst 1978 veröffentlicht wurde.[2] Unter dem Einfluss dieser Arbeit entwickelten Whitfield Diffie und Martin Hellman im Jahr 1976 den Diffie-Hellman-Schlüsselaustausch. Sie veröffentlichten die Forschungsarbeit unter dem Titel „New Directions in Cryptography“.[3] Das Verfahren sorgte für einen gewaltigen Schub in der Kryptographie, eine Wissenschaft, die damals noch nicht sehr lange öffentlich betrieben wurde.[4] Ursprünglich nannten die Forscher das Verfahren ax1x2. Martin Hellman schlug 2002 vor, das Verfahren Diffie-Hellman-Merkle-Schlüsselaustausch zu nennen, „wenn schon Namen damit verbunden werden“, in Anerkennung von Ralph Merkles Anteil an der Entwicklung asymmetrischer Verfahren.[5]
Die Bedeutung dieser Entwicklung wird auch mit der kopernikanischen Wende verglichen: „Die Entwicklung der asymmetrischen Verschlüsselung hat für die Kryptographie eine vergleichbare Bedeutung wie die Kopernikanische Wende für die Astronomie und stellt neben der Digitalisierung der Informationen und dem Internet als Kommunikationsplattform ein Fundament des dritten Jahrtausends dar.“[6]
Whitfield Diffie und Martin Hellman prägten mit dem Verfahren auch einen neuen Sicherheitsbegriff in der Kryptographie, der darauf basiert, dass kein effizienter Algorithmus für die Kryptoanalyse existiert: Ein Kommunikationsprotokoll ist sicher, wenn dessen Kryptoanalyse so viel Zeit und Arbeit bedeutet, dass diese in der Praxis nicht ausgeführt werden kann.[7] Die Sicherheit des Diffie-Hellman-Merkle-Schlüsselaustauschs beruht entscheidend darauf, dass die diskrete Exponentialfunktion in gewissen zyklischen Gruppen eine Einwegfunktion (englisch one-way function) ist, so insbesondere in der primen Restklassengruppe. Das heißt, dass in dieser die Exponentiation effizient berechenbar ist, für deren Umkehrung, den diskreten Logarithmus, jedoch bis heute kein effizienter Algorithmus bekannt ist.
Das Diffie-Hellman-Merkle-Verfahren ist mittlerweile nur eines von vielen Verfahren, die die diskrete Exponentialfunktion (mit diskretem Logarithmus als Umkehrung) als Einwegfunktion nutzen. Man spricht in diesem Zusammenhang auch von Krypto-Systemen auf Basis des diskreten Logarithmus oder einfach von DL-Verfahren.[8] So ist es beispielsweise eng verwandt mit dem Elgamal-Verschlüsselungsverfahren, das 1985 vom Kryptologen Taher Elgamal entwickelt wurde. Dieses ist im Prinzip nichts anderes als ein DHM-Schlüsselaustausch mit anschließendem Senden einer Nachricht, die mit dem vereinbarten Schlüssel verschlüsselt ist.[9]
Die Forscher führten in der fundamentalen „New Directions“-Arbeit auch das Konzept einer digitalen Signatur ein: Ein Sender berechnet mit Hilfe eines geheimen Signaturschlüssels (dem Private Key) zu einer digitalen Nachricht (d. h. zu beliebigen Daten) einen Wert, der digitale Signatur genannt wird. Dieser Wert ermöglicht es jedem, mit Hilfe des öffentlichen Verifikationsschlüssels (dem Public Key) die nichtabstreitbare Urheberschaft und Integrität der Nachricht zu prüfen.[10] So entstand als Weiterentwicklung des DHM-Schlüsselaustauschs eine vielfältige Familie an digitalen Signaturen auf Basis des diskreten Logarithmus. Zu den Bekanntesten gehören das Elgamal-Signaturverfahren und der Digital Signature Algorithm.[11]
Neben der Einwegfunktion entwickelten Whitfield Diffie und Martin Hellman auch das Konzept der Falltür (englisch trapdoor). Das ist eine „versteckte Abkürzung“ durch eine Zusatzinformation, mit der die ansonsten schwierige Umkehrung einfach gemacht wird. Auf der Basis von Falltürfunktionen lassen sich asymmetrische Verfahren entwickeln, bei denen die Übertragung eines geheimen Schlüssels nicht mehr notwendig ist. Damit leisteten sie auch wichtige Vorarbeiten zur Entwicklung des RSA-Kryptosystems. Ronald L. Rivest, Adi Shamir und Leonard Adleman versuchten eigentlich zu beweisen, dass es ebensolche Falltürfunktionen nicht geben kann. Bei den Beweisversuchen stießen sie jedoch tatsächlich auf eine solche Einwegfunktion mit Falltür. Das führte 1977 zur Entwicklung des berühmtesten Public-Key-Algorithmus, des nach den Initialen seiner Erfinder sogenannten RSA-Kryptosystems.[12]
Unterschiedliche Varianten des DHM-Verfahrens werden heute für die Schlüsselverteilung in den Kommunikations- und Sicherheitsprotokollen des Internet eingesetzt, wie z. B. IPsec (Internet Protocol Security), IPv6 (Internet Protocol Version 6) und TLS (Transport Layer Security). Diese dienen zur Sicherung bei der Übertragung von Datenpaketen der IP-Protokollschicht bzw. von Daten der Anwendungsebene, beispielsweise in den Bereichen des elektronischen Handels. Dieses Prinzip der Schlüsselverteilung besitzt damit eine wichtige praktische Bedeutung.[13] Der hier automatisch berechnete Schlüssel wird dann als Schlüssel für ein schnelles symmetrisches Verfahren wie Data Encryption Standard (DES) oder Advanced Encryption Standard (AES) verwendet.
Das Konzept der Public-Key-Kryptographie und einige spezifische Methoden waren bis 1997 durch die U.S. Patente 4.200.770 (Hellman, Diffie, Merkle, 1980) und 4.218.582 (Hellman, Merkle, 1980) geschützt, die der Stanford University gehören.[14][15] Für die Entwicklung der Public-Key-Kryptographie und der digitalen Signatur erhielten Whitfield Diffie und Martin Hellman im Jahr 2015 den Turing Award verliehen, der als höchste Auszeichnung in der Informatik gilt, vergleichbar dem Nobelpreis oder der Fields-Medaille.[16]
Geheime Kryptologie
Wie erst 1997 bekannt wurde, hatte das britische Government Communications Headquarters (GCHQ) schon in den 1960er Jahren den Auftrag erteilt, zur Vermeidung der hohen Kosten bei der damals üblichen Schlüsselverteilung einen anderen Weg zu finden. James H. Ellis formulierte das Konzept der „nicht-geheimen Verschlüsselung“. Daraus entwickelte Clifford Cocks ein Verfahren, das er bereits 1973 in einem internen Dokument beschrieb und das dem RSA-Verfahren sehr ähnlich ist. Somit muss aus heutiger Sicht der Dinge festgehalten werden, dass eigentlich Clifford Cocks als erster ein asymmetrisches Kryptoverfahren entwickelte. Diese Errungenschaft wird ihm nicht allgemein anerkannt, da seine Arbeit per definitionem Verschlusssache war und deshalb damals nicht veröffentlicht wurde. Erst 1997 wurde das interne Dokument auf der Website der Communications Electronics Security Group veröffentlicht.
In diesem Zusammenhang wurde auch bekannt, dass Malcolm Williamson, ein weiterer Mitarbeiter des GCHQs, schon 1975 das Schlüsselaustauschverfahren nach Diffie-Hellman entdeckte. Interessant ist dabei, dass die Entdeckung der beiden Verfahren – RSA und DHM – in der öffentlichen und der geheimen Kryptologie in umgekehrter Reihenfolge stattfand.[17]
Schlüsseltauschproblem
Verschlüsselungsverfahren, bei denen zwei Teilnehmer denselben geheimen Schlüssel verwenden, nennt man symmetrische Verfahren. Seien Alice und Bob Sender und Empfänger von Nachrichten über einen abhörbaren Kanal und sei Eve (von engl. eavesdropper, zu deutsch Lauscher/Lauscherin) ein Lauscher, der versucht, Nachrichten mitzulesen. Bei einem guten Verschlüsselungsverfahren ist es für Eve unmöglich, eine Nachricht ohne Kenntnis des Schlüssels zu entschlüsseln, selbst bei Kenntnis des Verschlüsselungsverfahrens. So besagt Kerckhoffs’ Prinzip, dass die Sicherheit eines Verfahrens allein auf der Geheimhaltung eines Schlüssels beruhen muss (und nicht auf der Geheimhaltung des Verschlüsselungsalgorithmus). Eine Nachricht, die verschlüsselt wird, heißt Klartext, der verschlüsselte Text Geheimtext.[18]
Wichtige Voraussetzung für eine sichere symmetrische Kommunikation ist also, dass der Schlüssel zwischen Alice und Bob bereits über einen sicheren Weg ausgetauscht wurde, beispielsweise durch einen vertrauenswürdigen Kurier oder bei einem direkten Treffen. Beim Schlüsseltauschproblem stellt sich nun folgendes Problem: Alice will mit Bob, der sich beispielsweise in Übersee befindet, mit einem symmetrischen Verschlüsselungsverfahren kommunizieren. Die beiden sind über eine unsichere Leitung verbunden und haben keinen Schlüssel ausgetauscht. Wie vereinbaren nun Alice und Bob über einen unsicheren Kanal einen gemeinsamen geheimen Schlüssel?[19]
Ein manueller Schlüsselaustausch hat den Nachteil, dass er recht unübersichtlich wird, wenn eine größere Anwendergruppe untereinander verschlüsselt kommunizieren will. Bei Kommunikationspartnern sind Schlüssel erforderlich, wenn jeder mit jedem kommunizieren will. Bei 50 Kommunikationspartnern wären somit insgesamt 1.225 Schlüssel nötig.[20]
Das Diffie-Hellman-Verfahren liefert eine elegante Lösung für diese Probleme: Es erlaubt Alice und Bob, einen geheimen Schlüssel über die öffentliche, nicht gesicherte Leitung zu vereinbaren, ohne dass Eve den Schlüssel erfährt.[19]
Mathematische Grundlagen
Hinweis: Die folgenden Betrachtungen vermitteln mathematische Grundlagen asymmetrischer Kryptoverfahren auf Basis des diskreten Logarithmus. Die einzelnen Abschnitte beschränken sich insbesondere auf die wesentlichen Aspekte, die für den Entwurf und die Sicherheitsanalyse des Diffie-Hellman-Merkle-Schlüsselaustauschs notwendig sind. Um eine gewisse Verständlichkeit zu wahren, werden einige Aspekte vereinfacht dargestellt. Für tiefergehendere Betrachtungen und Beweise sei auf die Literatur zu den mathematischen Grundlagen im Literaturabschnitt verwiesen.
Einwegfunktionen
Eine Einwegfunktion ist eine mathematische Funktion, die komplexitätstheoretisch „leicht“ berechenbar, aber „schwer“ umzukehren ist.[21] Eine mathematische Einwegfunktion muss folgende Eigenschaften aufweisen:
- Die Berechnung des Funktionswerts ist „einfach“, d. h. es existiert ein Algorithmus, der ihn in Polynomialzeit berechnen kann.
- Die Berechnung der Umkehrfunktion zu einem gegebenen Funktionswert , d. h. einem , sodass , ist allerdings „schwer“, d. h. es existiert kein „schneller“ Algorithmus für dieses Problem. „Schnell“ meint hier einen probabilistischen Algorithmus, der in Polynomialzeit läuft.
Einen anschaulichen Vergleich bietet ein klassisches Papier-Telefonbuch einer größeren Stadt: Die auszuführende Funktion ist die, einem Namen die entsprechende Telefonnummer zuzuordnen. Da die Namen alphabetisch geordnet sind, lässt sich dies ziemlich schnell durchführen. Aber ihre Invertierung, also die Zuordnung eines Namens zu einer gegebenen Telefonnummer, ist offensichtlich viel schwieriger.[22]
Man kann zeigen, dass Einwegfunktionen genau dann existieren, wenn P ≠ NP, die berühmte Vermutung aus der Komplexitätstheorie, gilt (siehe P-NP-Problem). Obwohl die Einwegfunktionen in der Kryptographie eine wichtige Rolle spielen, ist bis heute nicht bekannt, ob sie im streng mathematischen Sinne überhaupt existieren.[23]
Die Sicherheit des DHM-Schlüsselaustauschs basiert darauf, dass der diskrete Logarithmus in gewissen zyklischen Gruppen als Einwegfunktion angenommen wird. Es gibt dabei keine Falltür, d. h. eine Zusatzinformation, mit der die Umkehrfunktion leicht zu berechnen wäre. Im Gegensatz dazu verwendet beispielsweise das RSA-Kryptosystem mit der Faktorisierung eine Einwegfunktion mit Falltür.
Diskrete Exponentialfunktion und diskreter Logarithmus
Die diskrete Exponentialfunktion
liefert den Rest bei Division von durch m. Die Umkehrung der diskreten Exponentialfunktion heißt diskreter Logarithmus.
Die diskrete Exponentialfunktion ist auch für große Exponenten effizient berechenbar. Selbst für über hundert Bit lange Zahlen ist bei geschickter Implementierung eine Sekunde auf einem PC ausreichend. Zur effizienten Berechnung kann der Satz von Euler und das Square-&-Multiply-Verfahren verwendet werden.
Für die Umkehrung, also die Berechnung des Exponenten , bei gegebener Basis , Modul und gewünschtem Ergebnis, ist allerdings bis heute kein schneller Algorithmus bekannt: Selbst mit größtem Hardwareaufwand und den besten bekannten Algorithmen erreicht man bei mehreren Tausend Bit schnell Berechnungszeiten, die über die Lebensdauer unseres Universums hinausgehen.[24]
Bei der diskreten Exponentialfunktion handelt es sich nach heutigem Kenntnisstand somit um eine Einwegfunktion. Da es jedoch keinen mathematischen Beweis für deren Existenz gibt, wäre es theoretisch möglich, dass eines Tages ein schnelles Verfahren zur Berechnung des diskreten Logarithmus gefunden wird. Da dies jedoch schon seit längerem erfolglos versucht wird, kann man annehmen, dass dieser Fall nie eintreten wird.[24]
Beispiel:
Die diskrete Exponentialfunktion ordnet einem das Ergebnis von zu. Bei der Rechnung wird jeweils der Rest bezüglich des Moduls gebildet. Dadurch entsteht ein endlicher Zahlenraum . Für die Werte ist die Abbildung eindeutig. Der diskrete Logarithmus ist die Umkehrfunktion, also die Zuordnung von nach .
Gruppentheorie
Eine Gruppe ist ein Paar , bestehend aus einer Menge und einer assoziativen Verknüpfung auf , die ein neutrales Element hat und für die jedes Element von ein inverses Element besitzt. Wenn für eine Gruppe zusätzlich das Kommutativgesetz gilt, spricht man von einer abelschen Gruppe. Eine Untergruppe einer Gruppe ist eine Teilmenge von , die bezüglich der Verknüpfung selbst wieder eine Gruppe ist.
Beispielsweise bildet die Menge der ganzen Zahlen mit der Addition als Verknüpfung die (abelsche) Gruppe . Das neutrale Element der Addition ist die (Null) und das additiv Inverse einer Zahl ist ihre Gegenzahl . Die ganzen Zahlen sind bezüglich der Addition wiederum eine Untergruppe der rationalen Zahlen . Demgegenüber bilden die rationalen (und ganzen) Zahlen zusammen mit der Multiplikation keine Gruppe, weil die Zahl kein inverses Element bezüglich der Multiplikation besitzt. Wenn man jedoch aus entfernt, erhält man die (abelsche) Gruppe .
Eine zyklische Gruppe ist eine Gruppe, deren Elemente als Potenz eines ihrer Elemente dargestellt werden können. Unter Verwendung der multiplikativen Notation lauten die Elemente einer zyklischen Gruppe
- ,
wobei meint und das neutrale Element der Gruppe bezeichnet. Das Element wird Erzeuger oder Primitivwurzel der Gruppe genannt. Eine zyklische Gruppe besteht also nur aus Potenzen des Erzeugers :
Bei einer Gruppe wird die Mächtigkeit auch als Ordnung der Gruppe bezeichnet. Für eine endliche Gruppe ist die Ordnung also einfach die Anzahl der Gruppenelemente. Der Satz von Lagrange besagt, dass die Ordnung jeder Untergruppe einer endlichen Gruppe deren Mächtigkeit teilt.
Prime Restklassengruppe und Primitivwurzel
Die prime Restklassengruppe ist die Gruppe der primen Restklassen bezüglich eines Moduls . Sie wird als oder notiert. Die primen Restklassen sind genau die multiplikativ invertierbaren Restklassen und sind daher endliche abelsche Gruppen bezüglich der Multiplikation. Die Menge bildet beispielsweise mit der Multiplikation modulo als Verknüpfung keine Gruppe, selbst wenn die ausgenommen wird. Es gibt noch weitere Zahlen, die kein inverses Element haben, nämlich , und . Dies sind genau die Zahlen, die einen echten Teiler mit gemeinsam haben. Die verbleibenden Elemente bilden schließlich die Multiplikative Gruppe
In der Kryptographie sind vor allem jene Zahlen von Interesse, für die alle Zahlen zwischen und ein inverses Element modulo haben. Dies ist genau dann der Fall, wenn eine Primzahl ist (weshalb man statt schreibt). Die Zahlen zwischen und bilden also zusammen mit der Modulo-Multiplikation die Gruppe . Eine weitere Aussage, die sich beweisen lässt: Nimmt man ein beliebiges Element aus und betrachtet die Menge , dann erhält man eine Untergruppe (mit als Generator der Untergruppe). Jede Untergruppe von hat mindestens einen Generator, und damit auch selbst. Die Gruppe ist also zyklisch.[25] Zum Beispiel ist eine zyklische Gruppe mit der als Generator, denn jede Zahl von bis lässt sich als Potenz von darstellen:[26]
Für als Generator erhält man dagegen nur die Untergruppe mit den Elementen :
Es lässt sich nun leicht nachvollziehen, dass die Gleichung immer lösbar ist, wenn ein Generator von ist, wobei dann ein Element von ist (außer ). Der diskrete Logarithmus existiert also in immer dann, wenn die Basis ein Generator von ist.[27] Stellt man die Zahlen in einem Kreis (Zyklus) der Potenzen dar, scheinen sie willkürlich verteilt zu sein. Dies gibt zumindest eine Vorstellung davon, weshalb der diskrete Logarithmus so aufwändig zu bestimmen ist.[28]
Man nennt ein erzeugendes Element von auch Primitivwurzel zum Modul . Die Zahl ist also eine Primitivwurzel modulo , die Zahl dagegen nicht. Es lassen sich alle Elemente der primen Restklassengruppe modulo als Potenzen von darstellen. In der Folge der Potenzen von modulo wiederholen sich jedoch die Reste (siehe oben).
Für eine Primzahl gibt es genau Primitivwurzeln , wobei für die Eulersche Phi-Funktion steht, die für jede natürliche Zahl die Anzahl ihrer teilerfremden natürlichen Zahlen angibt.
Für ist und , woraus folgt, dass es Primitivwurzeln modulo gibt (nämlich , , und ).
Es ist zwar bewiesen, dass für jede Primzahl genau verschiedene Primitivwurzeln modulo existieren, es ist aber kein Algorithmus bekannt, der auch effizient eine beliebige Primitivwurzel berechnen kann. Wenn gegeben und die Faktorisierung von unbekannt ist, so kann man immerhin testen, ob es sich bei einer Zufallszahl um eine Primitivwurzel modulo handelt. Es muss gelten:
- und für .
Für kryptographisch relevante Primzahlen ist eine solche Überprüfung aufgrund der Größe von nicht durchführbar.
Ist dagegen die Primfaktorzerlegung von bekannt, so ist genau dann eine Primitivwurzel modulo , wenn gilt
- für alle Primfaktoren .
Besonders einfach wird der „Primitivwurzel-Test“, wenn mit einer Primzahl gilt. Dann braucht man nur zu testen, ob
- und
ist. Trifft dies zu, ist eine Primitivwurzel modulo .[29]
Beispiel:
Sei . Dann ist mit , also prim. Um zu testen, ob eine beliebige Zahl eine Primitivwurzel modulo ist, muss und überprüft werden. Für gilt beispielsweise und . Also ist eine Primitivwurzel modulo . Die Weiteren sind 7, 10, 11, 14, 15, 17, 19, 20 und 21. Mit lässt sich einsehen, dass damit (alle 10) Primitivwurzeln modulo gefunden sind.
Funktionsweise
Veranschaulichung der Grundidee anhand gemischter Farben
Zunächst soll die Grundidee des Diffie-Hellman-Merkle-Schlüsselaustauschs anhand von „Farbmischen“ anschaulich dargestellt werden, wie es die Illustration veranschaulicht. In Wirklichkeit wären die Farben Zahlen und das Mischen von Farben entspräche der diskreten Exponentialfunktion.
Das Mischen von Farben wird hier als eine Einwegfunktion aufgefasst: Es ist „leicht“, zwei oder mehrere verschiedene Farben zu mischen. Die Umkehrung, das Zerlegen einer Farbmischung in ihre ursprünglichen Farb-Komponenten, ist jedoch sehr aufwändig, das heißt nicht effizient durchführbar.
Alice und Bob einigen sich zunächst öffentlich auf eine gemeinsame Farbe (im Beispiel Gelb). Außerdem wählt jeder der beiden Kommunikationspartner für sich eine geheime Farbe (Alice Orange und Bob Türkis). Bob und Alice mischen nun jeweils die gemeinsame Farbe mit ihrer geheimen Farbe. Im Beispiel entsteht dabei für Alice Beige und für Bob Graublau. Diese Farbmischungen tauschen Alice und Bob nun über die abhörbare Leitung aus. Einer potenziellen Lauscherin Eve ist es nicht effizient möglich, aus den öffentlichen Informationen (gelb, beige, graublau) auf die geheimen Farben von Alice und Bob zu schließen.
In einem letzten Schritt mischen nun Alice und Bob die Farbmischung ihres Gegenübers mit ihrer eigenen geheimen Farbe. Daraus entsteht wiederum eine neue Farbe (im Beispiel Ockerbraun), die für beide Kommunikationspartner gleich ist (gelb + orange + türkis = gelb + türkis + orange = ockerbraun). Somit haben Alice und Bob eine gemeinsame geheime Farbe. Für Eve ist es unmöglich, diese herauszufinden, da sie Alices und Bobs geheime Farbzutaten nicht kennt.
Mathematische Funktionsweise

a: privater Schlüssel von Alice
b: privater Schlüssel von Bob
p: öffentlich bekannte Primzahl
g: öffentlich bekannte natürliche Zahl kleiner als p
A: öffentlicher Schlüssel von Alice
B: öffentlicher Schlüssel von Bob
K: geheimer Sitzungs-Schlüssel für Alice und Bob
Die beiden Kommunikationspartner Alice und Bob wollen über ein unsicheres Medium, etwa eine Kabel- oder Funkverbindung, verschlüsselt kommunizieren. Dazu soll ein symmetrisches Kryptosystem eingesetzt werden, für das beide jedoch zunächst einen gemeinsamen geheimen Schlüssel benötigen. Das DHM-Kommunikationsprotokoll sorgt dafür, dass sie einen geheimen Schlüssel berechnen können, ohne dass Dritte (Eve) diesen erfahren können. Den auf diese Weise errechneten Schlüssel können sie dann in Zukunft verwenden, um verschlüsselt mit einem symmetrischen Kryptosystem zu kommunizieren.
- Alice und Bob einigen sich zunächst öffentlich auf eine große Primzahl und eine natürliche Zahl , die kleiner als ist. Sich öffentlich darauf einigen bedeutet, dass jeder diese beiden Zahlen kennen darf (also auch potenzielle Lauscher wie Eve). Idealerweise handelt es sich bei um einen Erzeuger der zyklischen Gruppe , das Verfahren funktioniert aber auch, wenn einen anderen Wert kleiner annimmt. In der Praxis ist es ohnehin meist so, dass und vorgegeben sind und von vielen Anwendern verwendet werden.[30]
- Alice und Bob erzeugen jeweils eine geheimzuhaltende Zufallszahl (privater Schlüssel) bzw. aus der Menge . und werden nicht übertragen, bleiben also potenziellen Lauschern, aber auch dem jeweiligen Kommunikationspartner, unbekannt. Nur Alice kennt die Zahl und nur Bob kennt die Zahl .
- Alice berechnet mit ihrer geheimen Zahl den öffentlichen Schlüssel und schickt an Bob. Bob berechnet mit seiner geheimen Zahl den öffentlichen Schlüssel und schickt an Alice.
- Alice erhält von Bob und berechnet mit ihrem privaten Schlüssel die Zahl . Bob berechnet mit dem erhaltenen und seinem privaten Schlüssel ebenfalls die Zahl . Die beiden haben die gleiche Zahl berechnet. Diese ist somit der gesuchte gemeinsame Schlüssel .
Nur Alice und Bob kennen . Eve kann aus der abgehörten Kommunikation nicht berechnen. Dazu müsste sie den diskreten Logarithmus lösen, was nach heutigem Kenntnisstand nicht effizient möglich ist, wenn die Zahlen groß genug sind. Alice und Bob können also gefahrlos für eine symmetrische Verschlüsselung nutzen.[30]
Dass beide Kommunikationspartner denselben Wert für berechnen, zeigen die folgenden beiden Restklassengleichungen[31]:
- .
- .
Da die Multiplikation kommutativ ist, gilt des Weiteren
und somit
- .
Alice und Bob erhalten also nach ihren jeweiligen Berechnungen die genau gleiche Zahl, nämlich den geheimen Schlüssel .
Beispiel:
Das folgende Beispiel dient zur Veranschaulichung und benutzt deshalb sehr kleine Zahlen. In der tatsächlichen Anwendung werden dagegen Zahlen mit mindestens mehreren hundert Stellen benutzt.
- Alice und Bob einigen sich auf die beiden öffentlichen Schlüssel und ( ist ein Generator der Gruppe , siehe Abschnitt „Gruppentheorie“).
- Alice wählt die Zufallszahl als geheimen Schlüssel und Bob .
- Nun berechnet Alice und sendet an Bob. Bob berechnet und sendet an Alice.
- Alice berechnet . Bob berechnet .
- Beide erhalten das gleiche Ergebnis .
Die Lauscherin Eve kann zwar die Zahlen 13, 2, 6 und 9 mithören, das eigentliche gemeinsame Geheimnis von Alice und Bob bleibt ihr aber verborgen. kann als Schlüssel für die nachfolgende Kommunikation verwendet werden.
Mit Hilfe der abgefangenen Nachrichten kann Eve immerhin die folgenden Gleichungen aufstellen:
Daraus kann sie beispielsweise durch Ausprobieren die beiden geheimen Zahlen und bestimmen. Den vereinbarten Schlüssel von Alice und Bob kann sie nun mit
ausrechnen.
Wenn jedoch die Primzahl groß genug gewählt wird und ein Generator der Gruppe ist, ist es für Eve zu aufwändig, um alle Zahlen zwischen und durchzuprobieren, die als Resultat der modularen Potenz in Frage kommen.[32]
Programmierung
Das folgende Programm in der Programmiersprache Python zeigt die Implementierung des Diffie-Hellman-Schlüsselaustauschs für und .
from random import randint
# Festlegung der Gruppe:
p = 107
g = 3
# Zufällige Wahl der geheimen Schlüssel von Alice und Bob:
a = randint(1,p-1)
b = randint(1,p-1)
# Berechnung der Öffentlichen Schlüssel:
A = pow(g, a, p)
B = pow(g, b, p)
print(f'Öffentlicher Schlüssel von Alice: {A=}')
print(f'Öffentlicher Schlüssel von Bob: {B=}')
# Berechnung des gemeinsamen Geheimnisses:
k_a = pow(B, a, p)
k_b = pow(A, b, p)
print(f'{k_a=}')
print(f'{k_b=}')
Sicherheit
Diffie-Hellman-Problem
Computational-Diffie-Hellman-Problem (CDH)
Angenommen, die Lauscherin Eve erfährt an der unsicheren Leitung die Zahlen , , und , aber nicht die diskreten Logarithmen von und von zur Basis . Mit der Kenntnis von und wäre es für sie eine leichte Aufgabe, den Schlüssel zu bestimmen. Die Zahlen und herauszufinden ist jedoch sehr schwer, wenn die Zahlen , und sehr groß sind, beispielsweise Zahlen mit mehreren hundert Stellen im Dezimalsystem.[7] Aus dieser Problemstellung ergibt sich das Computational-Diffie-Hellman-Problem:
- Wenn ein Element einer Gruppe und die Werte und gegeben sind, welchen Wert hat dann , mit unbekannt ?
Da dieses Problem in bestimmten Gruppen nur mit enormem Rechenaufwand zu lösen ist, kann ein Angreifer aus den beiden beim Diffie-Hellman-Merkle-Schlüsselaustausch übertragenen Nachrichten nicht den erzeugten Schlüssel berechnen.
Das Diffie-Hellman-Problem ist eng verwandt mit dem Diskreter-Logarithmus-Problem. Diskrete Logarithmen zu berechnen ist die einzige bekannte Methode, um das DHM-Verfahren zu brechen. Solange dies nicht in vertretbarer Zeit lösbar ist, ist es für einen Angreifer unmöglich, den geheimen Schlüssel zu bestimmen. Es ist allerdings nicht bewiesen, dass dies tatsächlich die einzige Methode ist, ob also jemand, der das Diffie-Hellman-Problem lösen könnte, auch diskrete Logarithmen effizient berechnen könnte.[33] Ueli Maurer hat gezeigt, dass beide Probleme zumindest unter bestimmten Voraussetzungen äquivalent sind.[34]
Decisional-Diffie-Hellman-Problem (DDH)
Soll es für einen Angreifer unmöglich sein, aus den öffentlich verfügbaren Informationen irgendwelche Informationen über den transportierten Schlüssel zu gewinnen, muss das Decisional-Diffie-Hellman-Problem (DDH) unangreifbar sein. Dieses Problem lässt sich folgendermaßen beschreiben:
- Ein Angreifer erhält drei Zahlen: , und . Dabei wurden entweder , und zufällig und gleichverteilt in gewählt oder gesetzt. Im zweiten Fall heißt Diffie-Hellman-Tripel. Der Angreifer muss entscheiden, ob ein solches Tripel vorliegt oder nicht. Kann er das nicht, ist es ihm unmöglich, aus und Rückschlüsse auf zu ziehen.[35]
Das Problem besteht also darin, bei gegebenem , und zu entscheiden, ob ist.
Wer das Computational-Diffie-Hellman-Problem lösen kann, ist offensichtlich auch dazu in der Lage, das Decisional-Diffie-Hellman-Problem zu lösen. Für den umgekehrten Fall ist das nicht klar.
Bei einer Auswahl von als Primitivwurzel kann das Decisional-Diffie-Hellman-Problem angegriffen werden. Dies liegt in folgendem Theorem begründet:
- Sei eine Primzahl, sei eine Primitivwurzel modulo und seien . Dann ist genau dann ein quadratischer Rest modulo , wenn oder ein quadratischer Rest ist modulo .
Das Theorem folgt daraus, dass eine Potenz von genau dann ein quadratischer Rest modulo ist, wenn der Exponent gerade ist.[33]
Ein Angreifer kann also prüfen, ob das Kriterium aus diesem Theorem erfüllt ist. Er kann zwar nicht immer entscheiden, ob ein Diffie-Hellman-Tripel vorliegt, er antwortet aber zu 75 % richtig. Sein Vorteil gegenüber reinem Raten beträgt also 50 %.[36]
Wahl der öffentlichen Zahlen
DHM-Primzahl p
Die Sicherheit des Verfahrens basiert nicht zuletzt auf der Länge der gewählten Zahlen. So muss die Primzahl dermaßen gewählt werden, dass diskrete Logarithmen modulo mit derzeit bekannten Methoden nicht (effizient genug) berechnet werden können. Je größer die verwendete Primzahl, desto sicherer das Verfahren, aber auch desto aufwendiger.[37] Das Bundesamt für Sicherheit in der Informationstechnik empfiehlt im Fall eines Einsatzzeitraum[s] über das Jahr 2022 hinaus für eine Schlüssellänge von mindestens 3000 Bit (Stand 2017).[38]
Die DHM-Primzahl muss zudem so gewählt werden, dass Algorithmen zur Berechnung des diskreten Logarithmus kein leichtes Spiel haben. So muss beispielsweise vermieden werden, dass nur kleine Primfaktoren hat. Ansonsten kann nämlich der Pohlig-Hellman-Algorithmus angewendet werden, der nicht von der Gruppenordnung, sondern vom größten Faktor der Gruppenordnung abhängt. Außerdem sollte für das Zahlkörpersieb möglichst ungeeignet sein. Dies ist der Fall, wenn es ein irreduzibles Polynom vom Grad 5 gibt, das sehr kleine Koeffizienten und eine Nullstelle hat.[39]
„Generator“ g
Die Zahl sollte so gewählt werden, dass alle Zahlen zwischen und als Resultat der modularen Potenz in Frage kommen. Erst dann ist es zu aufwändig, alle Zahlen durchzuprobieren (wenn darüber hinaus die Primzahl groß genug gewählt worden ist). Diese Eigenschaft erfüllt die Zahl , wenn sie ein Primitivwurzel zum Modul ist, d. h. ein Erzeuger der Gruppe .[26] Wenn Alice und Bob beispielsweise wählen, so funktioniert das Verfahren zwar noch immer, doch der Schlüssel ist auf jeden Fall , denn ist genau der Generator der Untergruppe von mit einem Element. Ähnlich unsicher ist das Verfahren, wenn Alice und Bob für einen Generator einer anderen kleinen Untergruppe wählen. Bei einem Generator einer großen Untergruppe ist das Verfahren sicherer, am besten wird ein Generator der ganzen Gruppe gewählt.[8]
Wie im Abschnitt „Prime Restklassengruppe und Primitivwurzel“ gezeigt, lässt sich eine Primitivwurzel relativ leicht finden, wenn man die DHM-Primzahl als mit einer Primzahl wählt. Wie jedoch im vorherigen Abschnitt gezeigt, kann das Decisional-Diffie-Hellman-Problem angegriffen werden, wenn man als Primitivwurzel wählt.
„Wählt man statt dessen so, dass die Restklasse von modulo Primzahlordnung hat mit einer hinreichend großen Primzahl , dann gilt DDH nach heutiger Auffassung als schwierig.“
Verwendung fester Gruppen und Primzahlen
Da die Erzeugung sicherer Primzahlen rechenaufwendig ist, verwenden viele Implementierungen eine feste Primzahl .[40] Einige Netzwerkprotokolle wie etwa Internet Key Exchange geben eine Liste von möglichen Gruppen und deren Primzahl vor.
Die Verwendung fester Gruppen und Primzahlen kann ein Angreifer ausnutzen, um einen Großteil der Berechnung zum Brechen des diskreten Logarithmus vorab durchzuführen und um mehrere Ziele gleichzeitig anzugreifen. Der Zahlkörpersieb-Algorithmus besteht aus vier Schritten, wobei die ersten drei Schritte lediglich die Primzahl benötigen. Ist bekannt, kann ein Angreifer somit den Großteil vorberechnen und die Ergebnisse für jeden auf basierenden Schlüsselaustausch wiederverwenden. Dadurch kann zum Beispiel der Logjam-Angriff in TLS, nach einer einwöchigen Vorberechnung, einen 512-Bit-DHM-Schlüsselaustausch in rund 70 Sekunden brechen.[40]
Nach Schätzungen eines Forscherteams kann ein Angreifer mit Vorberechnung der 10 häufigsten 1024-Bit-Primzahlen den Netzwerkverkehr von 66 % der VPNs, 26 % der SSH-Server, 16 % der SMTP-Server und 24 % der HTTPS-Websites im Internet entschlüsseln. Die Forscher schätzen, dass der Rechenaufwand zum Brechen von 1024-Bit-Diffie-Hellman von einem staatlichen Angreifer wie der National Security Agency aufgebracht werden kann.[40]
Man-in-the-Middle-Angriff
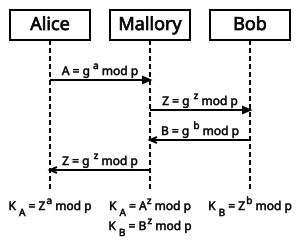
Der Diffie-Hellman-Merkle-Schlüsselaustausch ist nicht mehr sicher, wenn der Angreifer bei einem Man-in-the-Middle-Angriff Datenpakete verändern kann. Im Alice-und-Bob-Modell heißt ein solcher Angreifer, der aktiv in das Geschehen eingreifen kann, Mallory (von engl. malicious, dt. i. e. hinterhältig, heimtückisch). Mallory fängt bei einem Man-in-the-Middle-Angriff die von Alice und Bob gesendeten Nachrichten ab und sendet stattdessen jeweils seine eigene Nachricht
weiter, die er aus einer beliebigen Zahl und den öffentlich bekannten Zahlen und berechnet.
Nach dem Schlüsselaustausch besitzen die beiden Kommunikationspartner Alice und Bob unterschiedliche Schlüssel und . Im Prinzip wurde zweimal ein DHM-Schlüsselaustausch durchgeführt: einmal zwischen Alice und Angreifer Mallory und einmal zwischen Mallory und Bob. Dabei erlangt Mallory Kenntnis der beiden Schlüssel und .
Da Alice und Bob im weiteren Verlauf davon ausgehen, mit dem jeweils Anderen zu kommunizieren, kann Mallory die folgende symmetrisch verschlüsselte Kommunikation abhören. Diese leitet er dazu weiterhin über sich selbst um. Daten von Alice entschlüsselt Mallory mit und verschlüsselt sie wieder mit , bevor er sie an Bob weiterschickt. Dabei kann Mallory den Nachrichteninhalt sowohl lesen als auch unbemerkt verändern. Die gleiche Vorgehensweise wendet er auch für die Gegenrichtung an.
Um einen solchen Man-in-the-Middle-Angriff auszuschließen, müssen die ausgetauschten Nachrichten authentifiziert werden. Dazu wird ein Informationsvorsprung benötigt, der über einen authentifizierten Kanal erreicht wird.[41]
Seitenkanalangriffe
Ein Seitenkanalangriff bezeichnet eine kryptoanalytische Methode, die die physische Implementierung eines Kryptosystems in einem Gerät (z. B. einer Chipkarte, eines Security-Tokens oder eines Hardware-Sicherheitsmoduls) oder in einer Software ausnutzt. Dabei wird nicht das kryptographische Verfahren selbst, sondern nur eine bestimmte Implementierung angegriffen. Das Prinzip beruht darauf, ein kryptographisches Gerät bei der Ausführung der kryptologischen Algorithmen zu beobachten und Korrelationen zwischen den beobachteten Daten und dem verwendeten Schlüssel zu finden.
Zeitangriff
Im Jahr 1995 veröffentlichte Paul Kocher eine neuartige Methode, mit der es ihm gelang, Implementierungen von Diffie-Hellman, RSA und DSA zu brechen: der Zeitangriff (timing attack).[42]
Ziel des Zeitangriffs ist die diskrete Exponentialfunktion. Wenn eine Krypto-Implementierung für irgendwelche größeren Zahlen , und berechnet, dann geschieht dies fast immer mit dem Square-and-Multiply-Algorithmus. Bei diesem ist für jedes Bit von eine Aktion festgesetzt: Hat das gerade bearbeitete Bit den Wert , dann ist diese Aktion eine Multiplikation, ansonsten eine Quadrierung. Da die Rechenzeiten für die Multiplikationen länger dauern als für die Quadrierungen, kann Eve aus Zeitmessungen Rückschlüsse auf die Zahl der Einsen in ziehen. Variiert er die Zahl , reichen irgendwann die Informationen aus, um zu berechnen. Schon mit einigen Tausend Zeitmessungen lassen sich entsprechende Implementierungen mit 1024-Bit-Schlüsseln brechen.[43]
Um solche Zeitangriffe zu verhindern, müssen jedoch bei der Implementierung lediglich Verzögerungen in den Ver- bzw. Entschlüsselungsprozess eingebaut werden. Mit dem als Blinding genannten Verfahren wird zum Beispiel an einer Stelle des Verfahrens eine Zufallszahl eingerechnet, die an anderer Stelle wieder herausgerechnet wird. Eine andere Möglichkeit besteht darin, den Prozess so zu gestalten, dass er unabhängig vom Eingabewert immer gleich lange dauert.[44]
Stromangriff

Im Jahr 1998 stellten Paul Kocher, Joshua Jaffe und Benjamin Jun erstmals das Konzept des Stromangriffs vor.[45] Bei Stromangriffen wird nicht nur die Verarbeitungszeit gemessen, sondern mit einem Oszilloskop auch der Stromverbrauch. Besonders Smartcards sind gegenüber Stromangriffen anfällig, da diese auf eine externe Stromversorgung angewiesen sind. Ein Angreifer misst die Ver- und Entschlüsselungsvorgänge und versucht bestimmte Stellen der Stromverbrauchskurve einzelnen Bestandteilen des Verfahrens zuzuordnen. Auch hier ist der Square-and-Multiply-Algorithmus ein geeignetes Ziel, da sich bei diesem Multiplikationen und Quadrierungen am Stromverbrauch oft gut unterscheiden lassen. Stromangriffe sind etwas aufwendiger in der Durchführung als Zeitangriffe, gelten jedoch als wirkungsvoller.[46]
Als Gegenmaßnahme gegen Stromangriffe kann der Hersteller von Krypto-Modulen den Stromverbrauch verschleiern, indem er Dummy-Operationen in einen Ver- bzw. Entschlüsselungsvorgang einbaut. Eine weitere Möglichkeit besteht darin, ein künstliches Stromrauschen zu erzeugen, das den eigentlichen Stromverbrauch überlagert.[47]
Elliptic Curve Diffie-Hellman (ECDH)
Kryptosysteme auf Basis elliptischer Kurven (kurz ECC-Verfahren, von engl. Elliptic Curve Cryptography) sind keine eigenständige kryptographische Verfahren, sondern bekannte DL-Verfahren, die auf besondere Weise implementiert werden. Jedes Verfahren, das auf dem diskreten Logarithmus in endlichen Körpern basiert, lässt sich in einfacher Weise auf elliptische Kurven übertragen und somit zu einem Elliptic-Curve-Kryptosystem umformen. Dabei werden die beim Originalverfahren eingesetzten Operationen (Multiplikation und Exponentiation) auf dem endlichen Körper ersetzt durch Punktaddition und Skalarmultiplikation auf elliptischen Kurven. Das -fache Addieren eines Punktes zu sich selbst (also die Multiplikation mit dem Skalar ) wird mit bezeichnet und entspricht einer Exponentiation im ursprünglichen Verfahren. Das Prinzip wurde Mitte der 1980er Jahre von Victor S. Miller[48] und Neal Koblitz[49] unabhängig voneinander vorgeschlagen.
Körper
Ein Körper ist eine Menge versehen mit zwei inneren zweistelligen Verknüpfungen „“ und „“, die meist „Addition“ und „Multiplikation“ genannt werden. Ein Körper ist bezüglich der Addition und der Multiplikation ohne Null eine abelsche Gruppe und es gelten die Distributivgesetze. Der bekannteste Körper ist die Menge der reellen Zahlen , auf der Addition und Multiplikation in üblicher Weise definiert sind.
Für eine Primzahl bildet die Menge der Zahlen zwischen und sowohl mit der Modulo-Addition als auch mit der Modulo-Multiplikation ohne Null eine Gruppe. Die Restklassen ganzer Zahlen modulo , geschrieben oder , bilden somit einen endlichen Körper (auch Galoiskörper, engl. Galois field). Außerdem gibt es für jede Primzahl und jede natürliche Zahl (bis auf Isomorphie) genau einen Körper mit Elementen, der mit oder bezeichnet wird. In der Elliptic Curve Cryptography sind insbesondere die beiden Spezialfälle und von Bedeutung, also und . Mit diesen lassen sich ECC-Verfahren am besten realisieren.[50]
Elliptische Kurven

Eine elliptische Kurve (EC) ist eine Menge von Punkten mit Werten aus einem Körper , die eine kubische Gleichung der folgenden Form erfüllen:
Die (reellen) Koeffizienten und müssen dabei die Bedingung erfüllen, um Singularitäten auszuschließen.
Eine elliptische Kurve ist eine glatte algebraische Kurve der Ordnung 3 in der projektiven Ebene. Dargestellt werden elliptische Kurven meist als Kurven in der affinen Ebene, sie besitzen aber noch einen zusätzlichen Punkt im Unendlichen, der hier als (sprich „O“) bezeichnet wird, jedoch nicht mit dem Nullpunkt des Koordinatensystems zu verwechseln ist. Über dem Körper der reellen Zahlen bilden die Punkte eine Kurve in der reellen Ebene.[51]
Eine wichtige Eigenschaft elliptischer Kurven ist folgende: Schneidet eine Gerade eine solche Kurve, dann gibt es genau drei Schnittpunkte. Dabei treten folgende Fälle auf:
- Bei einer Geraden, die parallel zur -Achse verläuft, ist einer der drei Schnittpunkte .
- Bei einer Geraden, welche die Kurve berührt, wird der Berührpunkt als doppelter Schnittpunkt gezählt.
- Bei allen anderen Geraden sind die Schnittpunkte offensichtlich.[52]
Durch diese Eigenschaft lässt sich mit Hilfe elliptischer Kurven eine Gruppe definieren:
Sei die Punktmenge einer elliptischen Kurve, vereinigt mit dem Punkt im Unendlichen. Man definiert die Gruppenoperation, die üblicherweise als Punktaddition bezeichnet wird, wie folgt:
- Um die Summe zweier Punkte und zu berechnen, zeichne eine Gerade durch und (falls , zeichne die Tangente an EC durch )
- Finde den dritten Schnittpunkt dieser Geraden mit der Kurve EC. (Falls die Gerade parallel zur -Achse läuft, so ist dieser Schnittpunkt .)
- Die Summe ist der Punkt von EC, der durch Spiegelung von an der -Achse entsteht. Die Spiegelung von ist wiederum .[51]
Das neutrale Element der Gruppe ist . Es gilt für alle Punkte der elliptischen Kurve. Das Inverse eines Punktes erhält man, indem man an ihn eine Gerade anlegt, die parallel zur -Achse verläuft. Ist diese Gerade eine Tangente, dann ist der Punkt selbst sein inverses Element.[51][52]
Der Punkt wird mit bezeichnet, entsprechend definiert man als -fache Addition des Punktes . Ist nicht der -Punkt, kann auf diese Weise jeder Punkt der Kurve E erreicht werden (d. h., zu jedem Punkt auf der Kurve existiert eine natürliche Zahl mit ), wenn man die richtigen Erzeugenden der Gruppe kennt. (Siehe auch Abschnitt Gruppenoperation im Artikel „Elliptische Kurve“)
Die Aufgabe, aus gegebenen Punkten diesen Wert zu ermitteln, wird als Diskreter-Logarithmus-Problem der elliptischen Kurven (kurz ECDLP) bezeichnet. Es wird angenommen, dass das ECDLP (bei geeigneter Kurvenwahl) schwer ist, d. h. nicht effizient gelöst werden kann. Damit bieten sich elliptische Kurven an, um auf ihnen asymmetrische Kryptosysteme zu realisieren.
Sehr anschaulich ist die Konstruktion für , da die Punkte in der reellen Ebene ausgedrückt werden können. Diese Konstruktion kann jedoch auf jeden Körper übertragen werden. In der Kryptographie sind elliptische Kurven der Form und von Bedeutung.
Beispiel:
Sei die elliptische Kurve
über dem Körper gegeben.[53]
Es ist also und und es gilt . Die Menge aller mit und ist also zusammen mit eine elliptische Kurve über .
Daraus ergeben sich die folgenden Punkte:
| Punkte | |||
|---|---|---|---|
| und | , | ||
| – | – | ||
| und | , | ||
| und | , | ||
| und | , | ||
| – |
Diffie-Hellman auf Basis elliptischer Kurven
Bei Kryptosystemen auf Basis elliptischer Kurven werden statt Rechenoperationen in Rechenoperationen in oder verwendet. Wiederum existieren in diesen Körpern effiziente Algorithmen zur Berechnung der Potenzfunktion, für die Berechnung des Logarithmus dagegen nicht.
Statt auf einen Modulus müssen sich Alice und Bob nun auf eine bestimmte elliptische Kurve einigen, d. h. auf einen Körper (bzw. ) und eine darauf aufbauende Gruppe (bzw. ). Alle Parameter, die im Exponenten stehen, sind (wie bisher) natürliche Zahlen, während die Basis einer Potenz ein Element von ist.[54]
Eine Exponentiation über ist aufwendiger als eine Exponentiation über , da sie sich aus mehreren Rechenoperationen in zusammensetzt. Dafür ist auch die Berechnung des Logarithmus in wesentlich „schwieriger“. Der zentrale Vorteil bei der Verwendung von ist daher, dass Alice und Bob bei gleicher Sicherheit eine Gruppe kleinerer Mächtigkeit verwenden können. Dies hat kürzere Schlüssellängen, kürzere Signaturen und kürzere Rechenzeiten zur Folge.[54]
Die Komplexität des Logarithmus nimmt in mit linear zu, in dagegen „nur“ logarithmisch. Eine Schlüssellänge von 1.024 Bit auf Basis des diskreten Logarithmus kann beispielsweise durch Verwendung elliptischer Kurven auf 200 Bit verkürzt werden, ohne dass dabei Sicherheitseinbußen entstehen. Die Einsparung an Rechenzeit wird meist um einen Faktor 10 angegeben.[54]
Ephemeral Diffie-Hellman
Im Zusammenhang des Verschlüsselungsprotokolls Transport Layer Security (TLS) bezeichnet Ephemeral Diffie-Hellman (englisch ephemeral: kurzlebig, flüchtig) die Verwendung von Diffie-Hellman mit jeweils neuen Parametern für jede neue TLS-Sitzung. Bei statischem Diffie-Hellman werden für jede TLS-Sitzung dieselben Parameter wiederverwendet, die sich aus einem Public-Key-Zertifikat herleiten. In beiden Fällen wird derselbe Algorithmus verwendet und lediglich die Parameter unterscheiden sich.
Die Verwendung von Ephemeral Diffie-Hellman zur Aushandlung eines symmetrischen Sitzungsschlüssels bietet Forward Secrecy, im Gegensatz zur verschlüsselten Übertragung eines Sitzungsschlüssels mit einem Public-Key-Verschlüsselungsverfahren, zum Beispiel RSA.
Literatur
Allgemeiner Überblick
- Albrecht Beutelspacher: Geheimsprachen. Geschichte und Techniken. 3., aktualisierte Auflage, C.H. Beck: München, 2002.
- Albrecht Beutelspacher, Jörg Schwenk, Klaus-Dieter Wolfenstetter: Moderne Verfahren der Kryptographie. Von RSA zu Zero-Knowledge. 8. Auflage, Springer Spektrum: Berlin, Heidelberg, 2015.
- Thomas Borys: Codierung und Kryptologie. Facetten einer anwendungsorientierten Mathematik im Bildungsprozess. Vieweg+Teubner: Wiesbaden, 2011.
- Johannes Buchmann: Einführung in die Kryptographie. 6. Auflage, Springer Spektrum: Berlin, Heidelberg, 2016.
- Karin Freiermuth, Juraj Hromkovič, Lucia Keller, Björn Steffen: Einführung in die Kryptologie. Lehrbuch für Unterricht und Selbststudium. 2. Auflage, Springer Vieweg: Wiesbaden, 2014.
- Klaus Schmeh: Kryptografie. Verfahren, Protokolle, Infrastrukturen. 5., aktualisierte Auflage, dpunkt.verlag: Heidelberg, 2013.
- Simon Singh: Geheime Botschaften. Die Kunst der Verschlüsselung von der Antike bis in die Zeiten des Internet. 13. Auflage, dtv Verlagsgesellschaft: München, 2016 (Englische Originalausgabe: The Code Book. The Science of Secrecy from Ancient Egypt to Quantum Cryptography. Fourth Estate: London, 1999).
Fachartikel
- David Adrian, Karthikeyan Bhargavan, Zakir Durumeric, Pierrick Gaudry, Matthew Green, J. Alex Halderman, Nadia Heninger, Drew Springall, Emmanuel Thomé, Luke Valenta, Benjamin VanderSloot, Eric Wustrow, Santiago Zanella-Béguelin, Paul Zimmermann: Imperfect Forward Secrecy: How Diffie-Hellman Fails in Practice. In: Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security. ACM, New York 2015, S. 5–17. (Online)
- Dan Boneh: The Decision Diffie–Hellman Problem. In: Proceedings of the Third Algorithmic Number Theory Symposium (Lecture Notes in Computer Science, Vol. 1423) Springer-Verlag, 1998, S. 48–63. (Online)
- Whitfield Diffie, Martin E. Hellman: New Directions in Cryptography. In: IEEE Transactions on Information Theory 22, Nr. 6, 1976, S. 644–654. (Online)
- Martin E. Hellman: An overview of public key cryptography. In: IEEE Communications Magazine 40, Nr. 5, 2002, S. 42–49 (Online). Originalartikel: An overview of public key cryptography. In: IEEE Communications Magazine 16, Nr. 6, 1978, S. 24–32 (Online)
- Paul C. Kocher: Cryptanalysis of Diffie-Hellman, RSA, DSS, and Other Systems Using Timing Attacks. In: Advances in Cryptology, CRYPTO '95 (15th Annual International Cryptology Conference), Springer-Verlag, 1995, S. 27–31. (Online)
- Paul C. Kocher: Timing Attacks on Implementations of Diffie-Hellman, RSA, DSS, and Other Systems. In: Advances in Cryptology, CRYPTO '96 (Lecture Notes in Computer Science, Vol. 1109), Springer-Verlag, 1996, S. 104–113. (Online)
- Paul Kocher, Joshua Jaffe, Benjamin Jun: Introduction to Differential Power Analysis and Related Attacks. In: Advances in Cryptology—CRYPTO ’99, 19th Annual International Cryptology Conference. (Lecture Notes in Computer Science, Vol. 1666) Springer-Verlag: Berlin, 1999, S. 388–397. (Online)
- Ueli Maurer: Towards the equivalence of breaking the Diffie-Hellman protocol and computing discrete logarithms. In: Advances in Cryptology – Crypto '94. Springer-Verlag, 1994, S. 271–281, doi:10.1007/3-540-48658-5_26.
- Ralph C. Merkle: Secure Communications over Insecure Channels. In: Communications of the ACM 21, Nr. 4, April 1978, S. 294–299. (Online)
Anwendung
- Anatol Badach, Erwin Hoffmann: Technik der IP-Netze. Internet-Kommunikation in Theorie und Einsatz. 3., überarbeitete und erweiterte Auflage, Hanser: München, 2015.
- Wolfgang Ertel: Angewandte Kryptographie. 4. Auflage, Hanser: München, 2012.
- Patrick Horster (Hrsg.): Chipkarten. Grundlagen, Realisierung, Sicherheitsaspekte, Anwendungen. vieweg, 1998.
- Michael Welschenbach: Kryptographie in C und C++. Zahlentheoretische Grundlagen, Computer-Arithmetik mit großen Zahlen, kryptographische Tools. 2., überarbeitete und erweiterte Auflage, Springer: Berlin, Heidelberg, 2012.
Mathematische Grundlagen
- Eric Bach, Jeffrey Shallit: Algorithmic Number Theory. Volume 1: Efficient Algorithms. MIT Press: Cambridge (MA), London, 1996.
- Christian Karpfinger, Kurt Meyberg: Algebra. Gruppen, Ringe, Körper. 3. Auflage, Springer Spektrum: Berlin, Heidelberg, 2013.
- Ramanujachary Kumanduri, Cristina Romero: Number Theory with Computer Applications. Pearson: Prentice Hall, 1998.
- Paulo Ribenboim: Die Welt der Primzahlen. Geheimnisse und Rekorde. 2., vollständig überarbeitete und aktualisierte Auflage, Springer: Berlin, Heidelberg, 2011.
- Lawrence C. Washington: Elliptic Curves. Number Theory and Cryptography. Second Edition, Chapman & Hall / CRC Press: Boca Raton (FL), 2005, S. 95–97.
Weblinks
- Bundesamt für Sicherheit in der Informationstechnik (BSI): BSI – Technische Richtlinien: Kryptographische Verfahren: Empfehlungen und Schlüssellängen Version 2016-01, Stand 15. Februar 2016.
- ECRYPT II: European Network of Excellence in Cryptology II
- Steven Levy: The Open Secret – Public key cryptography – the breakthrough that revolutionized email and ecommerce – was first discovered by American geeks. Right? Wrong. In: WIRED (veröffentlicht: 4. Januar 1999; abgerufen: 9. Mai 2016)
Einzelnachweise
- ↑ So u. a. Yiu Shing Terry Tin u. a.: Provably Secure Mobile Key Exchange: Applying the Canetti-Krawczyk Approach. In: Rei Safavi-Naini, Jennifer Seberry: Information Security and Privacy. 8th Australasian Conference, ACISP 2003, Springer: Berlin, Heidelberg, 2003, S. 166–179.
- ↑ Ralph Merkle: Secure Communications over Insecure Channels. In: Communications of the ACM 21, Nr. 4, April 1978, S. 294–299.
- ↑ Whitfield Diffie, Martin Hellman: New Directions in Cryptography. In: IEEE Transactions on Information Theory.22, Nr. 6, 1976, S. 644–654.
- ↑ Schmeh: Kryptografie. 5. Aufl., 2013, S. 185.
- ↑ Martin E. Hellman: An overview of public key cryptography. In: IEEE Communications Magazine 40 (5), 2002, S. 42–49.
- ↑ Badach, Hoffmann: Technik der IP-Netze. 3. Aufl., 2015, S. 53.
- ↑ a b Freiermuth u. a.: Einführung in die Kryptologie. 2. Aufl., 2014, S. 200.
- ↑ a b Schmeh: Kryptografie. 5. Aufl., 2013, S. 187.
- ↑ Taher Elgamal: A public key cryptosystem and a signature scheme based on discrete logarithms. In: IEEE Transactions on Information Theory 31, 1985, S. 469–472. Siehe auch H. W. Lang: Kryptografische Protokolle:ElGamal-Verschlüsselung (erstellt: 19. Februar 2010, aktualisiert: 29. Mai 2015).
- ↑ Beutelspacher: Geheimsprachen. 3. Aufl., 2002, S. 54.
- ↑ Schmeh: Kryptografie. 5. Aufl., 2013, S. 204–209.
- ↑ Beutelspacher: Geheimsprachen. 3. Aufl., 2002, S. 53.
- ↑ Welschenbach: Kryptographie in C und C++. 2. Aufl., 2012.
- ↑ Patent US4200770A: Cryptographic apparatus and method. Angemeldet am 6. September 1977, veröffentlicht am 29. April 1980, Anmelder: Stanford University, Erfinder: Martin E. Hellman, Bailey W. Diffie, Raph C. Merkle.
- ↑ Patent US4218582A: Public key cryptographic apparatus and method. Angemeldet am 6. Oktober 1977, veröffentlicht am 19. August 1980, Anmelder: Stanford University, Erfinder: Martin E. Hellman, Raph C. Merkle.
- ↑ Association for Computing Machinery: Cryptography Pioneers Receive ACM A.M. Turing Award (abgerufen am 1. Mai 2016).
- ↑ Borys: Codierung und Kryptologie. 2011, S. 155–156.
- ↑ Schmeh: Kryptografie. 5. Aufl., 2013, S. 39–42.
- ↑ a b Ertel: Angewandte Kryptographie. 4. Aufl., 2012, S. 77; Buchmann: Einführung in die Kryptographie. 3. Aufl., 2004, S. 153.
- ↑ Schmeh: Kryptografie. 5. Aufl., 2013, S. 176.
- ↑ Ertel: Angewandte Kryptographie. 4. Aufl., 2012, S. 98–99; Buchmann: Einführung in die Kryptographie. 3. Aufl., 2004, S. 192.
- ↑ Beutelspacher, Schwenk, Wolfenstetter: Moderne Verfahren der Kryptographie. 8. Aufl., 2015, S. 16.
- ↑ Beutelspacher, Schwenk, Wolfenstetter: Moderne Verfahren der Kryptographie. 8. Aufl., 2015, S. 17 mit Verweis auf Jose L. Balcazar, Josep Diaz, Josep, Joaquim Gabarró: Structural Complexity I. Springer: Heidelberg, Berlin, 1988.
- ↑ a b Schmeh: Kryptografie. 5. Aufl., 2013, S. 184.
- ↑ Schmeh: Kryptografie. 5. Aufl., 2013, S. 181–183.
- ↑ a b Freiermuth u. a.: Einführung in die Kryptologie. 2. Aufl., 2014, S. 202.
- ↑ Schmeh: Kryptografie. 5. Aufl., 2013, S. 183.
- ↑ Freiermuth u. a.: Einführung in die Kryptologie. 2. Aufl., 2014, S. 202–203.
- ↑ Buchmann: Einführung in die Kryptographie. 6. Aufl., 2016, S. 67–68.
- ↑ a b Schmeh: Kryptografie. 5. Aufl., 2013, S. 185–186.
- ↑ Freiermuth u. a.: Einführung in die Kryptologie. 2. Aufl., 2014, S. 199.
- ↑ Freiermuth u. a.: Einführung in die Kryptologie. 2. Aufl., 2014, S. 200–202.
- ↑ a b Buchmann: Einführung in die Kryptographie. 6. Aufl., 2016, S. 190.
- ↑ Ueli Maurer: Towards the equivalence of breaking the Diffie-Hellman protocol and computing discrete logarithms. In: Advances in Cryptology – Crypto '94. Springer-Verlag, 1994, S. 271–281.
- ↑ Buchmann: Einführung in die Kryptographie. 6. Aufl., 2016, S. 190. Siehe ferner: Dan Boneh: The Decision Diffie–Hellman Problem. In: Proceedings of the Third Algorithmic Number Theory Symposium (Lecture Notes in Computer Science, Vol. 1423) Springer-Verlag, 1998, S. 48–63.
- ↑ Für einen Beweis siehe Buchmann: Einführung in die Kryptographie. 6. Aufl., 2016, S. 191–192.
- ↑ Buchmann: Einführung in die Kryptographie. 6. Aufl., 2016, S. 192–193.
- ↑ Bundesamt für Sicherheit in der Informationstechnik: BSI – Technische Richtlinien: Kryptographische Verfahren: Empfehlungen und Schlüssellängen Version 2016-01, Stand 15. Februar 2016.
- ↑ a b Buchmann: Einführung in die Kryptographie. 6. Aufl., 2016, S. 193.
- ↑ a b c Adrian u. a.: Imperfect Forward Secrecy: How Diffie-Hellman Fails in Practice. In: Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security. 2015, S. 5–15.
- ↑ Shafi Goldwasser, Mihir Bellare: Lecture Notes on Cryptography. 2008, Abschnitt 11.1.5 und 11.2.
- ↑ Paul C. Kocher: Cryptanalysis of Diffie-Hellman, RSA, DSS, and Other Systems Using Timing Attacks. In: Advances in Cryptology, Crypto '95 (15th Annual International Cryptology Conference), Springer-Verlag, 1995, S. 27–31. (Online)
- ↑ Schmeh: Kryptografie. 5. Aufl., 2013, S. 320–321.
- ↑ Schmeh: Kryptografie. 5. Aufl., 2013, S. 321.
- ↑ Paul Kocher, Joshua Jaffe, Benjamin Jun: Introduction to Differential Power Analysis and Related Attacks. In: Advances in Cryptology—CRYPTO ’99, 19th Annual International Cryptology Conference. (Lecture Notes in Computer Science, Vol. 1666) Springer-Verlang: Berlin, 1999, S. 388–397.
- ↑ Schmeh: Kryptografie. 5. Aufl., 2013, S. 321–322.
- ↑ Schmeh: Kryptografie. 5. Aufl., 2013, S. 323–324.
- ↑ Victor S. Miller: Use of Elliptic Curves in Cryptography. In: Advances in Cryptology – CRYPTO ’85 Proceedings (= Lecture Notes in Computer Science. 218). Springer, 1986, S. 417–426
- ↑ Neal Koblitz: Elliptic Curve Cryptosystems. In: Mathematics of Computation 48, Nr. 177, American Mathematical Society, 1987, S. 203–209.
- ↑ Schmeh: Kryptografie. 5. Aufl., 2013, S. 212.
- ↑ a b c Beutelspacher, Schwenk, Wolfenstetter: Moderne Verfahren der Kryptographie. 8. Aufl., 2015, S. 148.
- ↑ a b Schmeh: Kryptografie. 5. Aufl., 2013, S. 214–215.
- ↑ Washington: Elliptic Curves. 2. Aufl., 2008, S. 95–97.
- ↑ a b c Schmeh: Kryptografie. 5. Aufl., 2013, S. 215.



























![{\displaystyle [0,6]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b0c99f608fe4838dc2e6fd517321a0344a2ad44)