Diskussion:Ornstein-Uhlenbeck-Prozess
Stationarität
Ist der OU-Prozess nur schwach stationär? Meiner Meinung nach ist starke Stationarität gegeben. Und hängt Stationarität vom Anfangswert eines Prozesses ab? Von Stationarität im engeren Sinne kann man eigentlich grundsätzlich sprechen, wenn der Anfangswert aus der stationären Verteilung gezogen wird. Aber wenn ich mich an die Vorlesung von Zeitreihenanalyse erinnere, ist die Frage mit dem Anfangswert wohl eher ein philosophisches Problem, so dass ich den OU-Prozess als stark stationär bezeichnen würde. Das Gleiche gilt natürlich auch für Wurzel-Diffusionsprozesse. Ich habe bei Stationarität auch gelesen, das MA-Prozesse, jedoch nicht AR-Prozesse stationär sein sollen. Warum sind AR-Prozesse nicht stationär? --Smeyen Disk 10:36, 21. Dez 2005 (CET)
Verwaistes Bild
Bei den verwaisten Bildern gefunden, falls noch benötigt. --Gruß Crux 16:32, 28. Mai 2006 (CEST)
Unverständlich für nicht-Mathematiker
es ist ja bestimmt alles richtig, was da so steht, aber für mich ist das leider überhaupt nicht nachvollziehbar. Könnte das jemand mal in einfachen Worten beschreiben, worum es geht, bitte? Wikipedia ist eine Enzyklopädie und kein Fachwörterbuch für Experten.
Make article accessible to physicists, engineers, etc.
Dear mathematicians who wrote this article. As a mathematician, I appreciate your work. But I am also a physicist and have to say that this article is hard to understand for specialists from other sciences such as physics and engineering who also use OUPs. (We do no have to try to make this article accessible to just everybody, but we really should include the other specialists' viewpoints).
I have added a section on application of OUP in physics to the English version. If someone could also write a section on OUPs in engineering and signal processing (see above) that would be great.
So that's the new section:
Application in physical sciences: The OUP is a prototype of a noisy relaxation process. Consider for example a Hookean spring with spring constant whose dynamics is highly overdamped with friction coefficient . In the presence of thermal fluctuations with temperature , the length of the spring will fluctuate stochastically around the spring rest length ; its stochastic dynamic is described by an OUP with , , . In physical sciences, the stochastic differential equation of an OUP is rewritten as a Langevin equation
where is Gaussian white noise with .
Benjamin.friedrich (talk) 20:14, 25 April 2010 (UTC)
Deterministisch?
Im Artikel heißt es, dass der Integrand deterministisch ist. Ich bin jedoch der Meinung, dass aufgrund vom dWs dieser stochastisch ist. Was ist eure Meinung?
Das ist falsch! Der Integrator ist stochastisch, aber der Integrant ist deterministisch (nicht signierter Beitrag von 78.52.195.64 (Diskussion | Beiträge) 20:40, 26. Mai 2009 (CEST))
Lévy-Prozesse
- "Wird die definierende Differentialgleichung nicht von einer brownschen Bewegung, sondern von einem Lévy-Prozess angetrieben, so erhält man auch einen (nicht-gaußschen) Ornstein-Uhlenbeck-Prozess."
- In der Definition ist von einem Wiener-Prozess die Rede. Der Wiener-Prozess ist ein Lévy-Prozess (laut dem Lévy-Prozess-Artikel).
- Wenn "brownschen Bewegung" Synonym zu "Wiener Prozess" verwendet wird, ist die Aussage m.E. unsinng ("wenn der Laden keine Pullover verkauft, sondern nur Kleidung ...").
- Wenn wörtlich die Brownsche Bewegung gemeint ist, ist nicht mehr das gemeint was oben in der Definiton stand Wiener Prozess (was aber natürlich eng verwandt ist).
- Frage: Liege ich falsch, und wenn nein, was unterscheidet einen (nicht-gaußschen) Ornstein-Uhlenbeck-Prozess vom "normalen" Prozess? Ist der nicht-gaußche einfach eine Verallgemeinerung? und der "normale" Prozess ein Spezialfall (da der Wienerprozess ein Spezialfall des Lévy-Prozesses ist)? Grüße,--Qaswed 13:35, 15. Nov. 2011 (CET)
Fehler beim Abschreiben von der Referenz
Also ich versuche es jetzt nochmal ueber diesen Weg, nachdem meine Aenderung geloescht wurde: Im Abschnitt "Eigenschaften", der letzte Punkt, wurde einfach wortwoertlich aus Buch von Rogers/Williams abgeschrieben, was in dem Kontexts des Artikel dann falsch wird. Erstens ist der Parameter nicht definiert. Zweitens bezeichnet in der Referenz den integrierten Ornstein-Uhlenbeck Prozess und nicht den eigentlichen Orstein Uhlenbeck (OU) Prozess. Im Buch von Rogers und Williams wird der OU Prozess mit . Man muss also im Kontext dieses Artikels einen neuen Prozess, meinetwegen , wie es Barndorff-Nielsen and Shepard nennen [1] , definieren, welches der integrierte OU Prozess ist: Und zwar soll fuer alle gelten
Die Aussage aus dem Artikel gilt dann fuer den Prozess , wenn man und waehlt. Es ist hier keine andere Referenz verwendet worden, sondern nur die urspruengliche korrekt. Ich hoffe das die Aenderung deshalb bald moeglichst uebernommen wird, da die Referenz nicht fehlt, wie bei der Loeschung der Aenderung als Grund angegeben. (nicht signierter Beitrag von El rubio (Diskussion | Beiträge) 13:02, 28. Nov. 2011 (CET))
Einzelnachweise
- ↑ O. E. Barndorff-Nielsen and N. Shephard: "Integrated OU Processes and Non-Gaussian OU-based Stochastic Volatility Models", S. 280, In: Scandinavian Journal of Statistics, Volume 30, 2, S. 277–295, June 2003
Grafik - R-Code falsch?
Mir scheint, dass sich im R-Code ein Fehler eingeschlichen hat, In der 6. Zeile des Codes bei der Definition des OU Prozesses: oup[i+1]=oup[i] + theta*(mu-oup[i])*(to-from)/steps+sigma*rnorm(n=1,mean=0,sd=sqrt(sigma^2*(to-from)/steps))
Hier ist ein "sigma" zuviel, entweder "...+sigma*rnorm(n=1,mean=0,sd=sqrt((to-from)/steps))" oder "...+rnorm(n=1,mean=0,sd=sqrt(sigma^2*(to-from)/steps))"
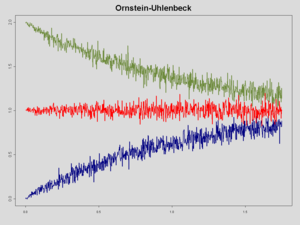
So zeigt das Bild einen OU Prozess mit den Parametern, theta = 1, mu = 1,2 und sigma = 0.09. (nicht signierter Beitrag von 84.179.138.234 (Diskussion) 21:34, 10. Jul 2014 (CEST))
Lévy-Prozesse
Der Paragraph macht keinen Sinn, da brownsche Bewegung (=Wiener-Prozess) ein Lévy-Prozess ist. Was ist eigentlich gemeint? (nicht signierter Beitrag von LoSchizzatore (Diskussion | Beiträge) 16:20, 9. Jun. 2016 (CEST))
- Das ist wohl als Verallgemeinerung gedacht, also so dass anstelle von auch ein anderer Lévy-Prozess verwendet werden kann, nicht unbedingt nur ein Wiener-Prozess. -- HilberTraum (d, m) 17:42, 9. Jun. 2016 (CEST)
- Ok, ich hab's mal umgeschrieben, hoffe das macht jetzt ein wenig mehr Sinn (bzw. ist ein wenig verständlicher).