Diskussion:Parallaxe

Der Text wurde aus "Das Handbuch zu KStars" Version 0.9.1 (URL: http://docs.kde.org/de/HEAD/kdeedu/kstars/index.html ) übernommen, auf das wesentliche verkürzt und leicht modifiziert --Fedi 18:04, 21. Okt 2003 (CEST)

Parallaxe in der Wissenschaftsgeschichte

Der Aspekt der Bedeutung der Parallaxe im Rahmen der Wissenschaftsgeschichte rund um die kopernikanischen Wende wird nicht beleuchtet. Man kannte den Effekt zwar, jedoch konnte man ihn bedingt durch die durch große Entfernungen nicht messen, was jedoch damals noch nicht bekannt war. Besitzt vielleicht jemand genug Kenntnisse um dieses Themenfeld auf brauchbarem Niveau zu ergänzen? --Saperaud 23:07, 25. Feb 2005 (CET)

Unklarer Satz im Abschnitt Parallaxe in der Fotografie

(Ich füge meine Frage hier ein, weil ich mit dem Handy arbeite und dieses nur die Edition kurzer Abschnitte erlaubt.)

Zum Ende des Abschnitts Parallaxe in der Fotografie hin steht:

Als Vertikalparallaxe wird hingegen eine fehlerhafte Ausrichtung der Bilder bezeichnet, bei dem die Augenachsen in etwas verschiedene Höhen blicken müssen.

Sollte es da einfach statt dem der heißen? Aber blicken können m.E. nur Augen, nicht Augenachsen. Deshalb vielleicht:

...bei der die Augenachsen in unterschiedliche Höhen gerichtet werden müssen? Hans Dunkelberg 17:30, 12. Nov. 2009 (CET)

Fehler ?

Mit der Parallaxenmessung wird die Entfernung zu anderen Himmelskörpern bestimmt. Wie groß ist eigentlich der wahrscheinliche Fehler, da ja nicht bekannt ist wie groß der Abstand zum Fixsternhimmel tatsächlich ist?. Diese Angabe fehlt mir im Artikel. --FALC 17:04, 16. Mai 2006 (CEST)

Justage der Messgeräte

Der größte Messfehler wird wohl in der Justage der Messgeräte liegen. Möglicherweise werden die Teleskope an Fixsternen ausgerichtet. Es sollte aber mal in den Artikel geschrieben werden wie es geht. Mir träumte nämlich schon dass ich wenn ich Geld habe eine 10 km breite Parallaxemaschine baue die mit Laser parallelisiert wird. Mit 10 km Basislinie kommt man aber nicht weit, selbst wenn man Präzisionswinkelmessung anwendet oder die Winkel mit Laser 10 km weit strahlt. Abstand Erde Sonne (1AE) würde damit ca 20 cm Abweichung von der Parallelität messbar machen wenn der Winkel 10 Km ausgestrahlt wird. --Matthias Pester Disk. (Matze6587) 04:14, 27. Aug 2006 (CEST)

Unklar!

Die erste Entfernungsmessung zum Mond wurde mittels der Parallaxenmessung durchgeführt. Was wäre, wenn der Mond 10-mal so groß wäre und 10-mal soweit entfernt wäre? Was würde man messen? Das Gleiche! Wenn er 1000- mal größer wäre und 1000- mal weiter weg, dann würde er hier genauso aussehen als wenn er so wäre wie er ist. Er würde sich nur schneller um die Erde bewegen. Die Umlaufzeit wäre die Gleiche! Da staune ich aber!!! (nicht signierter Beitrag von 88.74.187.168 (Diskussion) 01:10, 11. Apr. 2008)

Nicht aufgepasst! Im Artikel steht doch, dass eine Erdstrecke als Basis diente. Also wird der Mond bei weiterer Entfernung niemals gleiche Parallaxe erzeugt haben können. Auch steht nirgendwo, dass man verschiedene Punkt der Mondoberfläche (Durchmesser?) als Bezug nahm.--~~

Berechnung von parsec

Wäre es nicht sinnvoll im Artikel bei "Sternparallaxe" auch einen Rechenweg zu beschreiben, wie man vom Winkel 1 Bogensekunde auf die Sternentfernung kommt, in etwa so (als Beispiel eine einfache Möglichkeit): Radius der Erdbahn = 149,6 Mio. km, bei 1 Bogensekunde Paralaxe ist das 1/ 60 * 60 * 360 des Umfangs eines Kreises mit der Entfernung des Sternes als Radius, also

149,6 Mio. km * 60 *60 *360 = 2 * r * pi

193881600 Mio. km = 2 * r * pi

193881600 Mio. km / (2 * 3.14159) = r

30857215 Mio. km = r

r = 3,0857 * 10 hoch 13 km StephanPsy 00:00, 2. Jan. 2007 (CET)

Prinzip der Sternparallaxe: Durch die jährliche Bewegung der Erde um die Sonne verschiebt sich scheinbar ein naher Stern im Halbjahresrhythmus vor dem entfernten Hintergrund (stark übertrieben)

Kann mal jemand das Ganze etwas exakter mittels des altbekannten Strahlensatzes erläutern. Ist der Himmelskörper und auch der Fixsternhimmel jeweils 10 mal weiter entfernt und auch 10 mal größer als angenommen, ergibt sich ebenfalls eine Parallaxe von einer Bogensekunde, oder? Obige Rechnung setzt eine bekannte Größe voraus, den Radius der Umlaufbahn der Erde um die Sonne. O.k.. Aber wie hat man den bestimmt? Durch Parallaxenmessung etwa? O.k.. Aber welche bekannte Größe wurde dabei verwendet? (nicht signierter Beitrag von 88.74.189.223 (Diskussion) 21:58, 12. Apr. 2008)

Alle Theorie ist grau. Haben die Alten gesagt. fz JaHn 23:44, 12. Apr. 2008 (CEST)

Um das Problem über einen Größenvergleich mal anschaulich zu machen. Wie gesagt, die einzig bekannte Größe ist der Erdradius!!! (nicht signierter Beitrag von 88.74.179.89 (Diskussion) 02:17, 13. Apr. 2008)

1) Von zwei sehr weit entfernten Punkten auf der Erde aus (z. B. Südamerika und Japan) ist es kein Kunststück, die Entfernung der Sonne nach dem gleichen Prinzip sehr genau zu messen und zu berechnen.

2) Basis der astronomischen Parallaxe ist nicht "die jährliche Bewegung der Erde um die Sonne", sondern die "halbjährliche"! Gruß -- Dr.cueppers - Disk. 16:15, 10. Nov. 2008 (CET)

Radius ! Nicht Durchmesser

Quelle: Harald Lesch: Kosmologie für Fußgänger, S. 223: "Als Normbasis haben die Astronomen eine Strecke gewählt, die dem Radius der Erdbahn um die Sonne entspricht. Die Entfernung, aus der man diese Basis unter dem Winkel von einer Bogensekunde sieht, beträgt rund 30000 Milliarden Kilometer ... Diese Entfernung bezeichnet man in der Astronomie auch als parsec, abgekürzt pc." weitere Quelle siehe: http://lexikon.meyers.de/wissen/Parsec+(Sachartikel) StephanPsy 17:26, 1. Dez. 2008 (CET) weitere Quellen: persönliche Nachfrage bei befreundeten Berufsastronomen, siehe: http://www.astrotreff.de/topic.asp?TOPIC_ID=79189&whichpage=1 StephanPsy 18:00, 1. Dez. 2008 (CET)

Kommt auf den Kontext an.

Es ist ein wenig verwirrend weil hier zweimal der Begriff Basis auftaucht. Wenn ich eine Parallaxe messen will, dann wähle ich immer eine möglichst große Grundlinie (in der Regel als BasisLINIE bezeichnet) in einem gleichschenkligen Dreieck, also hier den Durchmesser.

Ich gebe mein Messergebnis aber als den halben Winkel dieses Messwertes, also den Winkel in einem rechtwinkligen Dreieck (mit dem Radius als BasisEINHEIT) an.

Der Artikel sollte also so angepasst werden, dass man durchaus vom Durchmesser als Methode der Messung spricht, aber vom Radius wenn es um die Definition des parallaktischen Winkels und insbesondere der Einheit Parsec geht.--89.49.94.129 04:28, 3. Dez. 2008 (CET)

Rechenbeispiel

Kann mal jemand ein mathematisches Beispiel liefern, wie man mittels der Parallaxe die Entfernung zum Mond ermittelt. Ich habe folgende Zahlen: Ich stehe 25 m von einer Hauskante entfernt. Der Mond berührt mit seiner rechten Seite diese Hauskante. Jetzt bewege ich mich 25 cm oder 0,25 m nach rechts. Der Mond berührt jetzt mit seiner linken Seite die Hauskante. Meine Bewegung nach rechts ist zur Entfernung zur Hauskannte also 1:100. Der Monddurchmesser und der Abstand zu mir und dem Mond sollte also auch im gleichem Verhältnis von 1:100 liegen. Da mir aber anderweitig weder Durchmesser onch Entfernung bekannt ist, ist mir völlig unklar wie man mittels der Parallaxe einen der beiden Werte bestimmen kann. --88.74.159.116 23:47, 9. Apr. 2009 (CEST)

In der Mathematik gilt: $a+b=c$ und <mat> a + d = c + x </math>. Somit gilt, $b=d+x$. D.h. die Parallaxe kann nur dann ein richtiges Ergebnis liefern, wenn a = Entfernung zur Hauswand, b = Wert der horizontale Bewegung des Auges und d = Entfernung zum Mond oder Durchmesser des Mondes bekannt sind. Wie einer der beiden letzten Werte bestimmt ist (wurde) ist mir auch schleierhaft. Nach dem originalem 3. Kepplerschen Gesetz: "Es ist sicher und ganz bestimmt..." kann wohl keiner der beiden Werte stimmen. --Reinstatistisch 00:37, 19. Apr. 2009 (CEST)

Projektion

Schon mal aufgefallen, daß das menschliche Auge alle Sterne am Himmel in gleicher Entfernung wahrnimmt? Auch Sonne und Mond liegen auf dieser seltsamen, kugelförmigen Projektionsfläche. Hat mal jemand versucht im (3D) Kino die Parallaxe eines Gegenstandes zu ermitteln? Noch einmal ganz genau den Einleitungsatz lesen!!! Bewege ich mich nach links erscheint logischerweise das von mir beobachtete Objekt weiter rechts. Je weiter dieses Objekt von mir weg ist, um so geringer ist die Parallaxe. Richtig auffällig wird diese Tatsache, wenn sich (weit) hinter meinem Objekt der Begierde ein Weiteres befindet, welches ich als Referenzpunkt nehme. Allerdings bewegt sich dieser Referenzpunkt tatsächlich auch nach rechts (wenn ich mich nach links bewege). Dies entspricht dem Relativitätsprinzip von Galilei. Den Einleitungssatz würde er glatt durchgehen lassen, den Rest des Artikels würde er vermutlich löschen. (Man soll Denken lehren, nicht Gedachtes! --MfG) (nicht signierter Beitrag von 88.74.165.50 (Diskussion | Beiträge) 00:50, 21. Okt. 2009 (CEST))

Richtig ist: "daß das menschliche Auge alle Sterne am Himmel in gleicher Entfernung wahrnimmt?" Dein Irrtum liegt hier: Weil der "(weit) hinter meinem Objekt der Begierde" (z.B. Mond) liegende Referenzpunkt (z.B. Stern in 200 Lj. Entfernung oder Quasar in 9 Milliarden Lj. Entf.) real nicht auf der Entfernung des wahrgenommenen Firmaments liegt, sondern eben sehr viel weiter entfernt, bewegt sich dieser Referenzpunkt tatsächlich NICHT auch nach rechts (wenn ich mich nach links bewege). StephanPsy 07:44, 21. Okt. 2009 (CEST) -typo- StephanPsy 11:16, 21. Okt. 2009 (CEST)

Diesen Einwurf kann ich nicht gelten lassen! Beweis: Die Venus (hoffentlich stimmt das) befindet sich derzeit (22.05.2010) gegen 22:15 Uhr deutlich sichtbar in NW. Von meinem Standpunkt aus befindet sich in ca. 200 m Entfernung ein Dach (ca. 20 m hoch). Auf diesem Dach ist ein Schornstein. Die Venus (Mittelpunkt) befindet sich exakt an der linken Schornsteinbegrenzung. Bewege ich mich einen Meter nach rechts, sehe ich die Venus exakt am rechten Schornsteinrand. Komischer Weise verhält es sich mit dem derzeit zunehmenden Mond genauso. Wechsle ich meine Position derart, daß ich den Mond (derzeit in SW) genau am linken Schornsteinrand (ich bin wieder 200 m von diesem entfernt) sehe und bewege mich einen Meter nach rechts, dann sehe ich den Mittelpunkt des Mondes ebenfalls am rechten Schornsteinrand. Genauso unverständlich ist die Tatsache, daß, wenn man verschiedene Sternbilder in Deutschland fotografiert und auf den Kanarischen Inseln und dann diese Bilder übereinander legt, keine Abweichungen erhält. Und das obwohl man aus völlig verschiedenen Winkeln auf unterschiedlich weit entfernte Sterne schaut. Mit einem Venustransit kann man weder die Entfernung der Erde von der Venus noch die Entfernung der Erde von der Sonne bestimmen. Strahlensatz! Es reicht ebend nicht nur den Erdradius zu kennen. Daher haben unsere Altväter diese Entfernungen nur in relativen und nicht in absoluten Zahlen angegeben. 88.74.130.98 23:00, 24. Mai 2010 (CEST)

---

weiß irgendwer was über 3D-Darstellungen mit einer "parallax barrier"? (http://en.wikipedia.org/wiki/Parallax_barrier) (nicht signierter Beitrag von 62.157.187.189 (Diskussion | Beiträge) 13:32, 16. Feb. 2010 (CET))

Betriff "Radius der Erdbahn" im Abschnitt "Jährliche Parallaxe, Sternparallaxe "

Da auch astronomisch etwas kleinere Lichter wie der Unterzeichnete den Artikel konsultieren, sollten Vereinfachungen erklärt sein. Die Erdbahn ist kein Kreis, "den" Erdbahnradius gibt es nicht (sondern unendlich viele, die sich aus der Nähe betrachtet, d.h. z.B. vom Mars aus, auch tatsächlich merklich unterscheiden). Daher vielleicht eher "mittlerer Erdbahnradius" usw. im Abschnitt "Jährliche Parallaxe, Sternparallaxe". - --Psychironiker 13:57, 22. Sep. 2010 (CEST)

Defekter Weblink (erl.)

http://www.br.de/mediathek/video/sendungen/alpha-centauri/alpha-centauri-entfernungen--2001_x100.html – GiftBot (Diskussion) 16:48, 27. Nov. 2015 (CET)

Der Link enthält nur einen kleinen Fehler, ...-entfernungen--2001_... sollte ...-entfernungen-2001_... heißen, http://www.br.de/mediathek/video/sendungen/alpha-centauri/alpha-centauri-entfernungen-2001_x100.html ist die funktionierende Version. (nicht signierter Beitrag von 80.108.33.53 (Diskussion) 00:19, 24. Feb. 2016 (CET))

Definition

Oft stöhnt man bei derartigen Artikeln ja nur auf über eine unverständliche Definition, und darum muss ich es hier doch wirklich mal ausdrücklich sagen: Gratulation zu dieser fantastischen, einfachen, in allgemeinverständlicher Sprache verfassten und auch für Laien gut nachvollziehbaren Definition! So sollte es überall sein! Danke an die Autoren! --217.239.9.5 10:08, 17. Okt. 2020 (CEST)

Das liest man gerne. Aber ich persönlich fand trotzdem noch Möglichkeiten der Verbesserung, und hab sie gleich angebracht. Bei Nichtgefallen einfach rückgängig machen! --Bleckneuhaus (Diskussion) 12:21, 17. Okt. 2020 (CEST)

Ah, ganz ehrlich, so weit hatte ich gar nicht gelesen. :D Ich war mit der Intro vollauf zufrieden. :-) --217.239.9.5 17:17, 17. Okt. 2020 (CEST)

Also, ich finde die Definitionen ein wenig verwirrend. In der Einleitung heißt es: "Als Parallaxe ... bezeichnet man die scheinbare Änderung der Position eines Objektes ..." Ein paar Zeilen später steht: "Definiert wird die Parallaxe als Winkel zwischen den Geraden ..." Einmal ist die Parallaxe also eine (scheinbare) Positionsänderung, dann wieder ein Winkel. Wenn die Parallaxe ein Winkel ist, wirkt die Bezeichnung "parallaktischer Winkel" (wie auch "Parallaxenwinkel") tautologisch; wenn die Parallaxe dagegen eine (scheinbare) Positionsveränderung ist, dann passt "parallaktischer Winkel" wieder, da die (scheinbare) Positionsveränderung vom Winkel abhängig ist. Lässt sich das irgendwie klären? --217.84.128.3 16:46, 26. Aug. 2021 (CEST)

Bewegung

Der Betrachter bewegt sich nach links. Obgleich die feststehenden Objekte deshalb nach rechts aus seinem Blickfeld verschwinden, scheinen sich die hinteren im Vergleich zu den vorderen nach links zu bewegen.

Bei der Parallaxe geht es um die Veränderung des Standorts des Betrachters, so dass er die Gegenstände aus verschiedenen Blickrichtungen sieht, wie für jemand der aus einem fahrenden Zug schaut, an dem die feststehenden Gegenstände draußen (Bäume, Felder, Gebäude usw.) sich scheinbar vorbei bewegen. Die ganz in der Nähe befindlichen Objekte bewegen sich scheinbar am schnellsten und verlassen das Blickfeld schneller als die weiter entfernten Objekte.

In der englischen Wikipedia gibt es Gifs, die die Bewegungen zeigen. Es wäre für die Verständlichkeit dieses Artikels von Vorteil, wenn auch wir Gifs verwenden würden.

Sänger hat vorschnell das von mir eingefügte Gif wieder entfernt. Er hat einfach geschrieben: "Nach links bewegt sich da gar nichts, nichtmal scheinbar." Er hat auch geschrieben, die Änderung von Sciencia58 wurde "verworfen". Danke für das verächtliche Wort "verworfen", man hatte auch "wegen Klärungsbedarf zurückgesetzt" schreiben können. Dass sich die Gegenstände nicht bewegen, hatte ich selbst geschrieben: "... die feststehenden Objekte ...". Die hinteren scheinen sich gegenüber den schnelleren vorderen nach links zu bewegen, auch wenn sie insgesamt ebenfalls nach rechts wandern. Die vorderen überholen die hinteren, daher bewegen sich die hinteren im Vergleich zu den Vorderen nach links. Das erkennt man daran, dass sie erst rechts des vorderen Objekts und dann links des vorderen Objekts zu sehen sind.

Prinzip der Sternparallaxe: Durch die jährliche Bewegung der Erde um die Sonne verschiebt sich ein naher Stern vor dem entfernten Hintergrund im Halbjahresrhythmus (hier stark übertrieben)

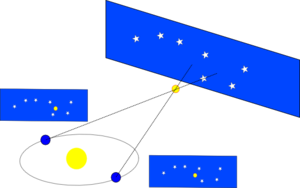
Zu den Effekten der Parallaxe gehört nicht nur, die scheinbare Bewegung eines Objekts durch die Veränderung der Perspektive des Betrachters oder die verschiedenen Blickrichtungen der Augen (Augenabstand), sondern auch die scheinbaren Unterschiede in den Bewegungen der Objekte untereinander, besonders in der Astronomie. Bei dem Bild mit dem roten Stern vor dem Großen Wagen kann man sagen, der rote Stern würde sich vor dem entfernten Hintergrund "verschieben", man kann ebensogut sagen, der Große Wagen würde sich im Vergleich zu dem roten Stern (ein Fixstern) verschieben. Sie verschieben sich beide nicht, jedenfalls nicht durch den Orbit der Erde um die Sonne. Die Verschiebungsrichtungen sind relativ zueinander zu sehen. Sciencia58 (Diskussion) 13:22, 29. Apr. 2022 (CEST)

Erstmal nur kurz hier: Verworfen ist die Vorgabe bei Nichtsichten, an dem Teil des Textes ändere ich nie was. --Grüße vom Sänger ♫ ^(Reden) 14:01, 29. Apr. 2022 (CEST)

Das Gif mit den "Wolkenkratzern" könnte weiter unten kommen, man soll den zweiten Schritt nicht vor dem ersten machen. Vielleicht gibt es ja eine Möglichkeit später mal die Artikel Parallaxe und Bewegungsparallaxe zusammenzuführen. Hier gibt es noch viel zu überlegen, auch weil die Parallaxe in der Einleitung als Positionsänderung definiert wird, im ersten Abschnitt aber als Winkel. Da müsste noch einiges geklärt werden, bevor es Sinn macht, hier weiter zu bearbeiten. Ich mache erstmal lieber nichts. Sciencia58 (Diskussion) 13:45, 29. Apr. 2022 (CEST)

noch eine

So, jetzt mal ein wenig inhaltlich.

Die Bildunterschrift war eindeutig falsch. Das .gif als allererstes in dem Artikel halte ich auch für suboptimal. Welches .gif eventuell unten weiter genommen werden könnte kann gerne diskutiert werden, aber dann gehört da mindestens eine korrekte Bildunterschrift dazu, in keinem der .gifs in der c:Category:Parallax animations bewegt sich irgendwas nach links, auch nicht scheinbar. Es bewegen sich verschiedene Objekte in augenscheinlich verschiedenen Abständen in verschiedenen Geschwindigkeiten von links nach rechts. --Grüße vom Sänger ♫ ^(Reden) 17:40, 29. Apr. 2022 (CEST)

Hier verschieben sich die pyramidenförmigen Berge hinter den Bäumen im Verhältnis zu den Bäumen nach rechts, während sie etwas langsamer als die Bäume nach links wandern. Ob man das erkennt, hängt davon ab, ob man etwas anderes als sich selbst in den Mittelpunkt stellen kann. Es gibt hier kein richtig oder falsch, weil beide scheinbar gegenläufigen Bewegungen gleichzeitig stattfinden. Hier ist allerdings nicht der Ort, um so eine Sachdiskussion zu vertiefen. Die Diskussionsseiten dienen dazu, über Möglichkeiten zur Verbesserung der Artikel zu beraten. Sciencia58 (Diskussion) 23:43, 29. Apr. 2022 (CEST)

Im Artikel sind nur sehr wenige von den kleinen eckigen Klammern mit so kleinen Zahlen drin. Das erste wäre, dass die sich mal vermehren müssten. Sciencia58 (Diskussion) 00:01, 30. Apr. 2022 (CEST)

Vielleicht solltet ihr alle mal etwas weniger aufeinander losgehen. Fakt ist Folgendes:

Parallaxe ist die Bezeichnung für eine in bestimmten Sachverhalten durch zwei verschieden definierte (Betrachtungs-) Richtungen (Vektoren) auf den gleichen (Bezugs-) Punkt auftretende, auf einer Projektionsebene, welche den Bezugspunkt nicht enthält, liegende Strecke(!). Eine Bewegung ist dafür nicht erforderlich! Es kommt nur auf zwei verschiedene Vektoren, eine Projektionsebene und einen Bezugspunkt außerhalb – in der Regel dazwischen –- an. Die beiden Vektoren bilden hierbei den Parallaxenwinkel. Beipiele:

1. Stell dir eine schmale Straße mit breiten Gehwegen an der Seite und Hausfassaden dahinter vor. An einem Straßenrand steht eine Straßenleuchte. Ein Beobachter macht von einer Stelle des gegenüberliegenden Straßenrandes ein Foto von der Straßenleuchte. Anschließend geht er einige Meter weiter und macht ein zweites Foto. Beim Vergleich der Fotos wird man feststellen, dass jeweils eine andere Stelle der Hausfassade (die Projektionsebene) direkt hinter dem Mast der Leuchte befindet. Der Abstand auf der Hausfasade ist hier die Parallaxe, der von den Fotopositionen und dem Mast gebildete Winkel ist der Parallaxenwinkel.
2. Parallaxe kann auch durch zwei gleichzeitige(!) Blickrichtungen definiert sein. Werden die beiden Fotos gleichzeitig von verschiedenen Personen angefertigt, so ist das Ergebnis das Gleiche wie im ersten Fall. Hier ist keinerlei Bewegung im Spiel.
3. Eine Parallaxe kann auch durch zwei Betrachtungsvektoren entstehen, von denen nur einr reell, die andere aber nur definiert ist. Bestes Beispiel ist der sogenannte Parallaxenfehler beim Ablesen analoger Messgeräte. Hier gibt es eine als richtig definierte Blickrichtung senkrecht zur Skalenebene und nur eine tatsächliche konstante Blickrichtung der ablesenden Person, welche bei geneigter Blickrichtung von der definierten abweicht und daher auf der Skala (die Projektionsebene) eine Parallaxe und damit einen Fehler erzeugt.
4. Eine Bewegung – also die kontinuierliche Änderung des Betrachtungsvektors – spielt hier nur insoweit eine Rolle, als dass sie die Pallaxe durch deren permanente Änderung für das menschliche Auge unmittelbar sichtbar macht. Würde im obigen ersten Beispiel mit der Straßenleuchte die Person eine Videoaufzeichnung starten und dann zum zweiten Punkt laufen, dann wäre auf dem Video rein optisch eine scheinbare Bewegung der Straßenleuchte in Relation zu Fassade zu sehen. Nur die Erfahrung, dass sich Straßenleuchten sehr selten und Fassaden noch seltener in der Straße herumbewegen, bewirkt, dass man das Video sofort als Bewegung der Kamera interpretiert. Die Erkennbarkeit einer Parallaxe ist davon unabhängig. Der Bezugspunkt der Bewegung ist also irrelevant.

Beim umstrittenen Gif liegen die Unterschiede in den Meinungen nur im Bezugspunkt der Bewegung. Ergo ist der Disput zwischen den Opponenten hier genauso irrelevant. Es ergibt sich daraus aber eine viel weitreichendere Erkenntnis: Bereits der erste Satz im Artikel ist in der jetzigen Form falsch, bzw. einschränkend! Man beachte weiterhin, dass die Ebene auch zwischen den Beobachtungspunkten und dem Bezugspunkt, also "im Vordergrund", liegen kann. ÅñŧóñŜûŝî (Ð) 02:10, 25. Sep. 2022 (CEST)

Keine totale SoFi am Nordpol?

"Wenn der Mondschatten die Erde in den Polregionen streift, findet dort prinzipiell nur eine partielle Finsternis statt."

Diese Aussage ist leider unbelegt und ich halte sie für falsch.

Bei Neumond wirft der Mond stets einen Schatten etwa in Richtung der Erde. Ob eine SoFi entsteht, hängt davon ab, ob dieser Schatten auf die Erde trifft oder drunter (unterhalb des Südpols) oder drüber (oberhalb des Nordpols) vorbeizieht. Wenn der Kernschatten des Mondes den Standort des Beobachters trifft, sieht dieser eine totale SoFi. Warum bitte sollte der Kernschatten niemals den Nordpol treffen? --2003:EC:9700:1F00:5C24:30A3:78A7:3661 12:09, 3. Sep. 2022 (CEST)

genauso sehe ich das auch. Die Aussage gehört rausgeworfen. -- Wassermaus (Diskussion) 21:47, 24. Sep. 2022 (CEST)

Das ist schon wegen der Erdachsneigung in dieser Formulierung Unsinn. Entweder an einem Punkt ist Kernschatten oder nicht. Was da wohl ausgesagt werden soll, ist wohl, dass es den Fall gibt, dass der Kernschatten die Erde knapp verfehlt und es dann dort im Halbschatten eine partielle Sofi geben kann, während es sonst auf der Erde gar keine Sofi gibt. Das ist aber eine andere als die bisherige Aussage. Ich habe es daher entfernt. ÅñŧóñŜûŝî (Ð) 00:54, 25. Sep. 2022 (CEST)