Diskussion:Phasenwinkel/Archiv

Diese Seite ist ein Archiv abgeschlossener Diskussionen. Ihr Inhalt sollte daher nicht mehr verändert werden. Benutze bitte die aktuelle Diskussionsseite, auch um eine archivierte Diskussion weiterzuführen.

Um einen Abschnitt dieser Seite zu verlinken, klicke im Inhaltsverzeichnis auf den Abschnitt und kopiere dann Seitenname und Abschnittsüberschrift aus der Adresszeile deines Browsers, beispielsweise

[[Diskussion:Phasenwinkel/Archiv#Thema 1]]

oder als Weblink zur Verlinkung auVorlage:SSerhalb der Wikipedia

https://de.wikiup.org/wiki/Diskussion:Phasenwinkel/Archiv#Thema_1

Allgemeinverständlichkeit

Wie bereits zuvor in der Diskussion angemerkt, erfüllt der Artikel in seiner derzeitigen Form nicht unbedingt das OmA-Kriterium. Ich würde in diesem Zusammenhang auch gerne auf den Schwesterartikel über Wellen hinweisen, wo man ja auf eine ähnliche Schwierigkeit stößt.160.45.25.162 00:30, 18. Apr. 2011 (CEST) Oder, auch dieser Hinweis kam schon, auf den Artikel in der englischsprachigen Wikipedia, der zwar allgemeinverständlicher aber nicht unbedingt schlechter ist.160.45.25.162 00:40, 18. Apr. 2011 (CEST)

Der erste Diskussionsbeitrag ist bald 5 Jahre alt und steht nach ca. 80 Bearbeitungen des Artikels in keinerlei Beziehung zum aktuellen Text. Der neue Diskussionsbeitrag nennt keinen einzigen konkreten Mangel. --Saure 12:38, 18. Apr. 2011 (CEST)

Aber Sie werden mir wohl zustimmen, dass der Artikel in dieser Form nicht sehr laienverständlich ist. Apropos Versionsgeschichte (beispielsweise 1. Oktober 2006): Warum wurden eigentlich die beiden Bilder entfernt? Oder warum gibt es am Anfang keinen Satz ähnlich diesem: Die Phase φ ist eine physikalische Kenngröße, durch die der Schwingungszustand einer Schwingung bestimmt ist. Gemäß Normung bezeichnet man als Phase... Nach meinem Eindruck hat sich die Einleitung des Artikels hinsichtlich der Laienverständlichkeit in den vergangenen fünf Jahren nicht zum besseren entwickelt. Der erste Satz beschreibt darüber hinaus völlig losgelöst vom physikalischen Phänomen lediglich eine mathematische Definition, auch das Wort veranschaulichen im folgenden Absatz halte ich in dem Zusammenhang für unglücklich gewählt. Ich will niemanden hier mit Rundumschlägen oder eigenmächtigen Aktionen vor den Kopf stoßen, aber ich habe vor einigen Jahren in einem neuen Artikel auf diesen hier verlinkt und bin mit der gegenwärtigen Situation etwas unglücklich.92.231.188.181 15:32, 18. Apr. 2011 (CEST)

Ich fühle mich nicht dazu in der Lage, auf ein "warum" für ca. 80 Änderungen verschiedener Verfasser zu antworten. Die ersten beiden Bilder der Fassung vom 1. Okt. 2006 kannte ich bisher nicht. Gut, dass sie entfernt worden sind. Der Erklärung im zweiten Bild „Sinusschwingungen unterschiedlicher Phasen“ ist falsch, denn es handelt sich um „Sinusschwingungen unterschiedlicher Phasenverschiebungswinkel“. Die Begriffe sollte man auseinander halten (viele können das nicht). Aber in seiner jetztigen Fassung werden sie deutlich gegeneinander gestellt. Auch der Einleitungssatz jener Fassung ist falsch. Schließlich ist der jetzt vorgeschlagene Einleitungssatz ebenfalls falsch, weil die Phase keine "Kenngröße" (darunter verstehe ich eine Konstante) ist, sondern eine Variable; φ = φ(t). Ich fürchte, dass der Artikel deshalb als nicht sehr laienverständlich deklariert wird, weil mit einer falschen Erwartung herangegangen wird, wie die Phase definiert sein möge, aber nicht ist. Die Normung ist aber eindeutig. --Saure 18:51, 18. Apr. 2011 (CEST)

Es braucht am Anfang einen anschaulichen und allgemeinverständlichen Satz (ähnlich vielleicht dem im Artikel unter Abgrenzung verwendeten)... zumindest sollte aber, um die Präzision zu erhöhen, im ersten Satz von einer Schwingungsfunktion anstatt bloß von einer Funktion die Rede sein. Ich halte es im übrigen für falsch, die Abbildungen aufgrund lediglich falscher Bildunterschriften gleich komplett zu entfernen und den Artikel damit der letzten Anschaulichkeit zu berauben.92.231.188.181 20:27, 18. Apr. 2011 (CEST)

OK, um die Diskussion abzukürzen verändere ich einfach die paar Kleinigkeiten am Artikel, und danach können wir uns gegebenenfalls hier wiedertreffen um Einwände und Verbesserungsvorschläge zu diskutieren.78.52.147.70 21:38, 18. Apr. 2011 (CEST)

@92.231.188.181: Zu den gelöschten Abbildungen kann ich nur wiederholen, dass ich sie nicht kannte; die Kritik am Löschen geht ins Leere. Ich bin ledigleich der Meinung, dass sie zum Thema „Phase“ nicht hilfreich sind, allen falls zum Thema „Phasenverschiebungswinkel“. Damit ist die Anschaulichkeit nichts wert, wenn sie das Falsche veranschaulicht. Zum Einleitungssatz sehe ich von dir einen Verbesserungsvorschlag, zu dem ich mir Gedanken machen werde. bloß heute habe ich keine Zeit dazu.

@78.52.147.70: Eine Diskussion kürzt man nicht dadurch, dass man sie in den Artikel verlagert. --Saure 08:54, 19. Apr. 2011 (CEST)

Hier der Vorschlag zur Erweiterung der Einleitung:

Harmonische Schwingungen sind Vorgänge, die sich zeitlich periodisch wiederholen und mathematisch mittels der Winkelfunktionen Sinus und Kosinus beschreiben lassen. Als Variable wird dazu statt der Zeit ein Winkel verwendet. Dieser wird gemäß der Normung als Phase oder genauer gesagt Phasenwinkel bezeichnet, wenn er linear von der Zeit abhängt.

Die harmonische Schwingung kann man sich veranschaulichen mit der Projektion einer Strecke auf die x-Achse, wenn die Strecke sich mit konstanter Winkelgeschwindigkeit um den Koordinatenursprung dreht. Die Länge der Projektion führt dabei die Schwingung aus, und der Phasenwinkel ist der linear mit der Zeit anwachsende Winkel der Strecke zur positiven Richtung der x-Achse.

--Saure 11:54, 20. Apr. 2011 (CEST)

Gefällt mir sehr gut! Ich hatte auch, Schande auf mein Haupt, übersehen, dass es zur Phasenverschiebung bereits einen eigenen Artikel gibt. In Anbetracht dessen macht es in der Tat nicht sehr viel Sinn, die beiden älteren Abbildungen zur Phasenverschiebung in den vorliegenden Text zu integrieren.160.45.25.162 11:10, 21. Apr. 2011 (CEST)

Falsche Verwendung des Begriffs Amplitude

die Amplitude ist nicht x(t),sondern X Dach (siehe bei Amplitude in der wikipedia), x(t) ist die augenblickliche Auslenkung oder der Funktionswert oder eben die Elongation, die weiter unten als neuer Begriff auftaucht, der ganze Text kommt sehr theorielastig daher, ich glaube nicht, dass er einem Unwissenden eine nützliche Information verschafft (am ehesten noch die Abbildungen) ich halte eine gründliche Überarbeitung für erforderlich (z.B. der Ausflug in die komplexen Zahlen mit der Eulerformel dürfte kaum zum Verständis beitragen, was die Phase nun wirklich ist), der Artikel in der englischen Wikipedia kommt mir deutlich besser vor --84.189.243.79 20:54, 21. Okt. 2006 (CEST)

Leider verstehe ich als Laie anhand dieses Artikels nicht, was eine Phase ist. Vielleicht kann man noch einen Teil einfügen, der halbwegs anschaulich darstellt, was man sich unter einer Phase vorzustellen hat. Falls das nicht geht, könnte ja kurz erläutert werden, warum man sich eine Phase nicht anschaulich vorstellen kann.

ich hab zwar auch nicht ganz verstanden was der artikel mir über die phase sagen will, find aber nicht, dass der "ausflug in die komplexen Zahlen" ganz ausgespart werden sollte, weil wikipedia ja auch nicht nur für laien da ist.

Hallo. 1. Die 2 Bilder sind nicht so das wahre. Es fällt auf das alle gezeichneten Schwingungen die gleiche Amplitude haben. Man könnte denken das "gleiche Amplitude" ein Kriterium dafür ist, das 2 oder mehr Schwingungen in Phase sind.
2. Ich würde ein Zeigerdiagramm zu 2 Phasenverschobenen Schwingungen einfügen, in dem man ganz einfach die 2 Phasen erkennen kann, und hinzu noch die Phasenverschiebung, also den Winkel im Bogenmaß zwischen den Zeigern. Wichtig auch hier: die Zeiger sollten unterschiedliche Längen (unterschiedliche Amplituden haben), damit man nicht auf die Idee komt, das die Amplitude irgendetwas mit der Phase zu tun hat.
3.Man könnte auch sagen die Phase ist einfach das Argument des sinus in der Schwingungsgleichung x(t)=A * sin (wt + phi)
4.Die Sache mit den komplexen Zahlen lässt sich denke ich gut mit punkt 2 in verbindung bringen. Wobei man noch Erläuterungen zum Zusammenhang komplexe Zahlen und Zeiger hinzufügen müsst.

Diese undatierte Diskussion hat ihren letzten Beitrag im April 2007.

Dieser Abschnitt kann archiviert werden. Saure 19:38, 15. Jun. 2011 (CEST)

Allgemeinverständlichkeit

Harmonische Schwingungen sind Vorgänge, die sich zeitlich periodisch wiederholen und mathematisch mittels der Winkelfunktionen Sinus und Kosinus beschreiben lassen. Soweit verständlich, sagt aber zum eigentlichen Lemma nichts aus. -->Gehört hier nicht her, schon gar nicht in die Einleitung.

Die variable Größe, von der eine Winkelfunktion unmittelbar abhängt (mathematisch als "Argument" einer Funktion bezeichnet), wird Phase bzw. in der Normung [1] [2] [3] [4] Phasenwinkel genannt. --> Viel zu abstrakt für die Einleitung. Das ist zwar richtig(?), aber völlig unverständlich für Nichtmathematiker. Der Hinweis auf die Normen gehört weiter unten in den Artikel, nachdem das Lemma allgemeinverstädnlich erklärt wurde. Und was soll überhaupt die allgemeine Betrachtung über die Größe, von der eine Winkelfunktion abhängt? Jede Winkelfunktion? Absolut unverständlich.

Diese Größe hängt bei einer harmonischen Schwingung linear von der Zeit ab. Sie hat die Dimension eines Winkels und wird meist im Bogenmaß, manchmal auch in Grad gemessen. Mit der Kreisfrequenz ω rotierende Strecke der Länge û ; die Phase φ(t) nimmt linear mit der Zeit zu --> Viel zu abstrakt formuliert.

Man kann sich solche Vorgänge veranschaulichen mit der Projektion einer Strecke auf die x-Achse, wenn die Strecke sich mit konstanter Winkelgeschwindigkeit um den Koordinatenursprung dreht. Der Endpunkt der Projektion führt dabei die harmonische Schwingung aus. --> Solche Vorgänge? Welche? Das ist Wischiwaschi, man kann sich gar nichts darunter vorstellen. Das Beispiel hilft hier nicht weiter. Es veranschaulicht die Harmonische Schwingung, sagt aber nichts darüber aus, was Phase bedeutet. Beispiele der Anwendung haben auch in der Einleitung nichts verloren, da gehört das Lemma ERKLÄRT, und zwar so daß es enzyklopädisch angemessen und ALLGEMEINVERSTÄNDLICH formuliert ist. --92.192.101.249 12:13, 9. Aug. 2013 (CEST)

Mein Vorschlag:

Der Phasenwinkel $\varphi$ ändert sich in Abhängigkeit zur Zeit

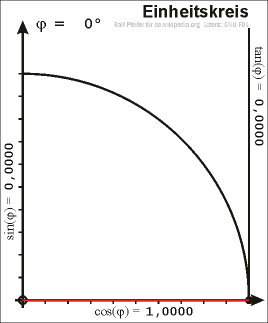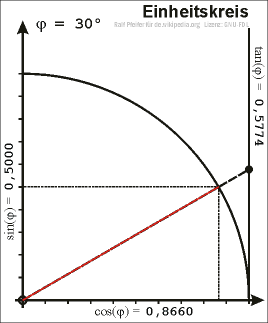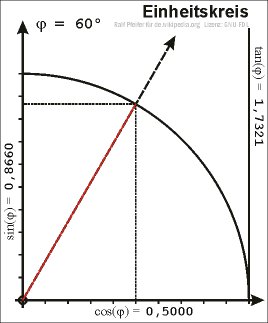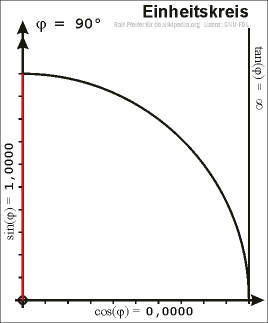
Als Phase oder Phasenwinkel $\varphi$ wird der Winkel bezeichnet, den bei harmonischen (also sinusförmigen) Schwingungen der Ortsvektor eines auf den Einheitskreis projezierten Kurvenpunktes der Schwingung mit der X-Achse einschließt. Dieser Winkel ist unmittelbar abhängig von der Zeit t und wird im Bogenmaß (rad) oder in Grad angegeben.

Als Bild würde ich vorschlagen, dieses hier zu verwenden. Darauf ist sehr anschaulich die Abhängigkeit von $\varphi$ von der Zeit und dem Schwingungsverlauf erkennbar.

Der Kosinus muß nicht eigens erwähnt werden, denn er ist ebenfalls sinusförmig.

Die Aussage zu den Normen würde ich vorschlagen, in einen eigenen Abschnitt Normung zu verschieben.

--92.192.101.249 13:06, 9. Aug. 2013 (CEST)

Vielleicht wäre auch dieses Bild von commons.wikimedia.org besser geeignet, leider ist es nicht animiert:

OndaSenoidal3.svg

Darauf ist der Zusammenhang von harmonischer Schwingung, Ortsvektor am Einheitskreis und eingeschlossenem Winkel $\varphi$ deutlicher erkennbar.

--92.192.101.249 13:21, 9. Aug. 2013 (CEST)

Ich finde Deinen Verbesserungsvorschlag nicht allgemeinverständlicher als die gegenwärtige Formulierung.

Alternativvorschlag:

Als Phase oder Phasenwinkel wird eine physikalische Größe bezeichnet, die den Zustand einer Schwingung beschreibt. Sie hängt bei harmonischen Schwingungen linear von der Zeit ab. Während einer Periode ändert sich die Phase um genau 2π. Die Momentanauslenkung der Schwingung ist dann direkt proportional zum Sinus bzw. Kosinus des Phasenwinkels. (usw.)

Das Zeigermodell, das die Beziehung zwischen der Rotation eines Zeigers, seiner Projektion und der Schwinung herstellt, muss man dann erst später einführen. Das kann in der Einleitung geschehen oder erst im Hauptteil des Artikels. --Pyrrhocorax (Diskussion) 15:00, 9. Aug. 2013 (CEST) Dieser Diskussionsbeitrag wurde von der Saure (ich vermute: versehentlich) gelöscht und von mir wiederhergestellt. --Pyrrhocorax (Diskussion) 18:02, 9. Aug. 2013 (CEST)

Sorry, ich habe zu dem Zeitpunkt an einer Antwort an dich gefeilt; dabei habe ich zwischen Artikel und Diskussion hin und her geblättert. Wie es dabei zur Löschung kommen konnte, ist mir unklar. --der Saure 20:01, 9. Aug. 2013 (CEST)

1. Zu einem Lemma gehört in die Einleitung das Umfeld, zu dem das Stichwort gehört. Das ist in diesem Fall die harmonische Schwingung.
2. „Die allgemeine Betrachtung über die Größe, von der eine Winkelfunktion abhängt“ gehört zum Kern des Verständnisses des Begriffs "Phase". Dass die Phase auch "Phasenwinkel" genannt wird, gehört zusammen mit der Fundstelle für diesen zweiten Begriff ebenfalls in die Einleitung. Elementare mathematische Grundkenntnisse, was eine Funktion oder eine Winkelfunktion ist, hast du vermutlich; auf diese wird hier aufgebaut.
3. „Solche Vorgänge? Welche? Das ist Wischiwaschi“. Wer im ersten Satz nicht zur Kenntnis nehmen will, dass es sich hier im harmonische Schwingungen handelt, ist an dieser Stelle allerdings am Ende. In dem Artikel wird etwas aufgebaut; etwas Lesen der Zusammenhänge gehört schon dazu.
4. Zu einer Bildunterschrift gehört die Erklärung der verwendeten Formelzeichen; alles Übrige dort ist Kurzaussage zum Text. Ich halte nichts von einem abstrakten "Einheitskreis". Hier geht es um physikalische Zusammenhänge mit konkreten physikalischen Größen.
5. „Beispiele der Anwendung haben auch in der Einleitung nichts verloren“; von solchen Anwendungen weiß ich nichts.
6. In einer weiter oben nachlasbaren Diskussion hat Benutzer:Eulenspiegel1 begründet, dass Winkel und Phasenwinkel zwei verschiedene Begriffe sind. Es ist nicht sinnvoll, wenn du den Phasenwinkel nun wieder als Winkel bezeichnen willst. --der Saure 20:01, 9. Aug. 2013 (CEST)

Den Punkten kann ich im Wesentlichen zustimmen. Nichtsdestotrotz hat die anonyme IP schon recht, dass der Einleitungsabschnitt nicht gerade ein Musterbeispiel an eleganter Formulierung und Allgemeinverständlichkeit ist. Was hältst Du also von meinem Alternativvorschlag? Zur Motivation: Er stellt nicht die Winkelfunktion an den Anfang, sondern die Linearität in der Zeit. Dadurch wird der etwas unverständliche Begriff "Argument" nicht benötigt und muss auch nicht kryptisch umschrieben werden. Außerdem können die Winkelfunktionen dann danach ganz zwanglos eingeführt werden. Meinungen? --Pyrrhocorax (Diskussion) 20:25, 9. Aug. 2013 (CEST)

Ich finde deinen Text eher vernebelnd. Bedenke: Wer (sinnvollerweise) nach einem Phasenwinkel fragt, bringt als Vorkenntnis ein Wissen über Winkelfunktionen mit. Hinter dem damit vorhandenen Niveau brauchst du nicht zurückzubleiben. --der Saure 13:01, 10. Aug. 2013 (CEST)

Ich finde den Begriff Argument nicht unverständlich. Man kann ihn ja auf Funktion (Mathematik verlinken, da steht im ersten Satz, was ein Argument ist.

Ich denke, Zustand einer Schwingung ist eher problematisch, ich mußte mir erst klar machen, daß Physiker den Begriff Zustand anders gebrauchen, als Laien. Das können wir nicht erwarten. Danke Saure, für Deinen Hinweis auf die Disk oben zur Unterscheidung von Winkel und Phasenwinkel. Das erklärt einiges. Und ihr habt recht, man kann es leider nicht so einfach und anschaulich vermitteln, wie ich mir das in meinem Vorschlag vorgestellt hatte. Schade eigentlich.

Meinen Hauptkritikpunkt, zu hoher Abstraktionsgrad des Artikeltextes muß ich wohl zurückziehen nachdem ich mir die Disk und weitere Quellen zu diesem Thema angesehen habe. Denn es handelt sich um ein abstraktes Konzept, das hier dargestellt werden soll. Das sollten wir dann aber auch dem Leser sagen, wenn er dem beim ersten Lesen etwas verschwurbelt anmutetenden Erklärungsklimzug zu folgen versucht. (ich betone: nur anmutend!). Es geht aber nicht, daß das Lemma erst klar wird, wenn man sich die gesamte Disk und weitere Quellen im Internet reinzieht.

Ich versuch's nochmal, diesmal auf euren Vorschlägen und dem vorhandenen Artikeltext aufbauend:

Als Phase oder Phasenwinkel (Formelzeichen $\varphi$) bezeichnet man allgemein die Argumente von beliebigen Winkelfunktionen. Der u.a. in der Normung verwendete Begriff Phasenwinkel ist abstrakt zu verstehen und verweist nicht auf einen geometrischen Winkel, auch wenn die Phase in einigen Sonderfällen als Winkel am Einheitskreis darstellbar ist. Als Begriff entstammt er der physikalischen Schwingungs- und Wellenlehre, und wird in vielen Bereichen der Physik, die sich mit harmonischen Schwingungen Schwingungsvorgängen befassen, verwendet.

Die Details zur Winkelfunktion, die genauen Normen, das Konzept mit dem Zeiger und auch die Idee mit dem Zustand einer Welle würde ich vorschlagen, dann weiter unten im Artikelbauch ausführlicher darzustellen, als es in kurzen Einführungssätzen möglich ist. Auch auf die Bereiche, in denen Phase konkret vorkommt, können wir da eingehen.

Grüße --92.193.93.230 15:47, 10. Aug. 2013 (CEST)

Saure, Du schreibst oben: Dass die Phase auch "Phasenwinkel" genannt wird, gehört zusammen mit der Fundstelle für diesen zweiten Begriff ebenfalls in die Einleitung. Ich hätte es z.B. genau umgekehrt gemacht, mir war der Begriff Phasenwinkel geläufig, und ich hätte eine Fundstelle für Phase gesucht, weil ich glaubte, das sei nur eine Abkürzung dafür aus dem Fachjargon der Elektrotechniker. Ich denke, wir lassen am besten beide Begriffe gleichwertig nebeneinander stehen.

Du schreibst außerdem (oben, an Eulenspiegel):Der Artikel wendet sich vorrangig an Elektrotechniker, und „in der Elektronik ist das nicht weiter wichtig. Das ist sachlich falsch. Der Begriff Phase ist außerhalb der Elektronik genauso wichtig für das Verständnis von Zusammenhängen in der (technischen) Akkustik, (siehe z.B. http://www.sengpielaudio.com/Rechner-LaufzeitPhase.htm), in der Strömungsdynamik, für die Wellennatur des Lichtes, etc. (das sind nur die, welche mir grade spontan einfallen). Du schreibst weiter unten: Wer im ersten Satz nicht zur Kenntnis nehmen will, dass es sich hier im harmonische Schwingungen handelt, ist an dieser Stelle allerdings am Ende. Ja, der ist am Ende. Und zwar u.a. weil es eben nicht immer nur um harmonische Schwingungen geht, wie in der Elektrotechnik und Elektronik. Wir können es uns also nicht so einfach machen, und nur die harmonischen Schwingungen abhandeln. Die müssen in einen eigenen Abschnitt, als Spezialfall, der sie sind. Und für die harmonischen Schwingungen eignet sich der Einheitskreis nunmal am besten zur Darstellung, wegen der Anschaulichkeit. Man sieht sofort den Zusammenhang zwischen Phasenwinkel und momentanem Zustand der Schwingung. Ich denke, auf den Einheitskreis können wir da nicht verzichten. Der Abschnitt könnte z.B. so aussehen und irgendwo unten im Artikelbauch kommen:

(neuer Abschnitt) Sonderfall harmonische Schwingung

Bei harmonischen, (also sinusförmigen) Schwingungen läßt sich der Zusammenhang von Phase und Welle graphisch darstellen, da hier Phasenwinkel und überstrichener Winkel $\varphi$ am Einheitskreis zusammenfallen. Hier entspricht die Phase dem realen Winkel, der vom Ortsvektor (oder sogen. "Zeiger") eines auf den Einheitskreis projezierten Kurvenpunktes der Schwingung mit der X-Achse eingeschlossen wird. Bei harmonischen Schwingungen ist der Phasenwinkel proportional zur Zeit t.

Phasenwinkel am Beispiel einer Sinuswelle

Gilt eigentlich der Zusammenhang $\varphi =\omega *t$ nur bei harmonischen Schwingungen, oder allgemein?

genug für heute.--92.201.32.15 04:40, 11. Aug. 2013 (CEST)

Der Artikel ist unter dem Begriff "Phase" entstanden. Als ich später auf diesen Artikel gestoßen bin und die Fundstelle für den Begriff gesucht habe, habe ich in den zugehörigen Normen dieser Begriff nicht gefunden, sondern nur "Phasenwinkel". Damit habe ich den Phasenwinkel, um niemanden zu verärgern, lediglich als gleichberechtigt in den Artikel eingefügt, dabei aber durch Angabe der Fundstellen kenntlich gemacht, welcher Begriff eigentlich verwendet werden sollte. Aber bei WP ist es egal, unter welchem der beiden Begriffe man anfängt zu suchen, man landet hier.

Wenn du anerkennst, dass der Phasenwinkel das Argument einer Sinus-Funktion ist, dann möchte ich gerne wissen, von welcher Sinusfunktion du sprichst, wenn du eine nicht harmonische Schwingung vor Augen hast. --der Saure 09:11, 11. Aug. 2013 (CEST)

Nochmal: Ich halte nichts von einem abstrakten Einheitskreis. Das ist ein Konstrukt der Mathematiker, die um Einheiten möglichst einen Bogen machen. Bei der physikalischen Größe Phasenwinkel haben auch der Kreisradius bzw. die Schwingungsamplitude eine Einheit; Kreis ja, aber Einheitskreis in diesem Zusammenhang nein. So ein Kreis ist im Artikel vorhanden, aber dazu hat sein Kreisradius nicht die normierte Größe 1, sondern die physikalische Größe û. Dabei bleit im Artikel offen, ob dieses û für eine elektrische oder mechanische Größe steht. --der Saure 13:46, 11. Aug. 2013 (CEST)

Unterschied zwischen Winkel und Phasenwinkel

Eine trigonometrische Funktion (gleichbedeutender Begriff: Winkelfunktion) ist grundsätzlich Funktion eines Winkels. Wenn dieser linear von der Zeit abhängt, heißt er Phasenwinkel. Genau dieses und nichts anderes ist der Unterschied zwischen Winkel und Phasenwinkel. Dass in einem Spezialfall auch einmal die abhängige Variable einer Winkelfunktion wieder ein Winkel sein kann, rechtfertigt nicht die Aussage, dass das der Unterschied zwischen Winkel und Phasenwinkel sei. --Saure 09:49, 4. Okt. 2011 (CEST)

Nein, die trigonometrische Funktion ist grundsätzlich eine Funktion von dimensionslosen Größen. Dies können Winkel sein, dies können aber auch Verhältnisse sein. Und ja: Wenn man den Sinus eines Winkels berechnet, dann ist der Winkel in diesem Kontext auch ein Phasenwinkel. Die Größe wäre also beides: Winkel und Phasenwinkel. Wenn man jedoch den Sinus eines Verhältnisses berechnet, dann wäre dieses Verhältnis zwar ein Phasenwinkel, aber kein Winkel.

Nein, ein Phasenwinkel muss nicht linear von der Zeit abhängen. Das tut er nur bei konstanter Kreisfrequenz. Wenn sich die Kreisfrequenz ändert, dann hängt der Phasenwinkel nichtlinear von der Zeit ab. --Eulenspiegel1 17:52, 4. Okt. 2011 (CEST)

Es ist doch völlig akademisch, darüber zu reden, was passiert, wenn die Konstante ω einmal keine Konstante ist. Die Definition des Phasenwinkels beschränkt sich ausdrücklich (auch in der wahrhaft breit angelegten DIN 1311-1) auf harmonische Schwingungen, „deren Argument eine lineare Funktion der Zeit ist“.

Der Artikel trigonometrische Funktion bezeichnet rechnerische Zusammenhänge zwischen Winkel und Seitenverhältnissen, aber die Seitenverhältnisse sind nicht das Argument der Funktion. Kannst du mir bitte wenigstens eine nicht an den Haaren herbeigezogene Anwendung zeigen, wo der Sinus ein Funktion eines Verhältnisses ist, das nicht für eine Winkel steht?

Was ist denn „eine reale Beziehung zwischen zwei Strahlen“? Werde doch bitte etwas konkreter, was für eine Beziehung du da meinst, egal ob real oder reell.

Der Satzteil, wonach „der Phasenwinkel das Argument einer trigonometrischen Funktion ist“, ist ebenfalls nicht zu halten, denn er hat erst einmal seine eigene Bedeutung. Dass ein Phasenwinkel genauso wie ein Winkel häufig als Argument einer trigonometrischen Funktion verwendet wird, ist aber eine andere Aussage. --Saure 18:27, 11. Okt. 2011 (CEST)

Schau dir zum Beispiel frequenzmodulierte Signale an. Dort ist ω keine Konstante. In dem Artikel Frequenzmodulation wird dann auch auf die "momentane Kreisfrequenz" eingegangen, die eben nicht konstant ist.

Hier noch ein Anwendungsbeispiel, bei der das Argument der trigonometrischen Funktion kein Winkel ist: Die Rotation auf einer echten Ellipse (mit $a\neq b$).

$z(t)=a\;\cos(\omega \;t)+i\cdot b\;\sin(\omega \;t)$

Dabei beträgt die Kreisfrequenz der Rotation $\omega$.

Der Winkel beträgt jedoch:

$\alpha (t)=\arctan \left({\frac {b\sin(\omega \;t)}{a\cos(\omega \;t)}}\right)=\arctan \left({\frac {b}{a}}\tan(\omega \;t)\right)$

Wenn wir uns diese Rotation anschauen wird auch schnell der Unterschied zwischen Kreisfrequenz und Winkelgeschwindigkeit klar:

Die Kreisfrequenz ist die Ableitung des Arguments der trigonometrischen Funktion und damit konstant ω. Die Winkelgeschwindigkeit ist dagegen die Ableitung des Winkels und für $a\neq b$ somit variabel.

Ich hoffe, bei diesem Beispiel wird klar, wieso α ein Winkel ist, ωt dagegen nicht. (Und wieso nur für den Spezialfall a=b gilt: α=ωt.)

Sicherlich kann man einen Winkel konstruieren, der den gleichen Wert hat wie ωt. Und sicherlich gibt es auch einen Vektor auf dem komplexen Einheitskreis, der modulo 2π den gleichen Wert hat wie ωt. Aber die Tatsache, dass ωt einen Wert größer als 2π annehmen kann, während Winkel immer einen Wert zwischen 0 und 2π annehmen, sollte deutlich machen, dass ωt kein Winkel ist.

Und um deinen Einwand gleich vorwegzunehmen, ja, man kann einen Einheitsvektor rotieren lassen. Und ja, wenn man den komplexen Vektor $e^{i\omega t}$ nimmt, dann hat dieser Vektor bzgl. der realen Achse den Winkel ωt. Aber nur weil zwei Sachen den gleichen Wert haben, heißt das noch lange nicht, dass sie gleich sind:

• $z(t)=a\cos(\omega \;t)+i\cdot b\sin(\omega \;t)$ ist eine elliptische Rotation, die eine Kreisfrequenz von ω hat und eine Winkelgeschwindigkeit von ${\dot {\alpha }}(t)$.
• ${\tilde {z}}(t)=e^{i\omega t}$ ist eine Kreisrotation, die eine Winkelgeschwindigkeit von ω hat.

z(t) und ${\tilde {z}}(t)$ sind zwei vollkommen unterschiedliche Bewegungen: Das eine ist eine Kreisbewegung und das andere ist eine Ellipse. Die Tatsache, dass die Kreisfrequenz von z genau so groß ist wie die Winkelgeschwindigkeit von ${\tilde {z}}$ sagt nichts darüber aus, dass beides identisch wäre. (Dass Ruhenergie und kinetische Energie in bestimmten Situationen gleichgroß sind, sagt auch nichts darüber aus, dass die beiden Energieformen identisch sind.)

Und bei ${\tilde {z}}$ gibt der Wert ωt auch tatsächlich einen Winkel an. Aber bei z selber gibt ωt keinen Winkel an sondern nur die Phase. (Bei ${\tilde {z}}$ sind Phase und Winkel praktischerweise identisch. Bei z unterscheiden sich jedoch Phase und Winkel.) --Eulenspiegel1 20:51, 11. Okt. 2011 (CEST)

Der Artikel beschränkt sich ausdrücklich auf harmonische Schwingungen, in denen die Fälle, die du hier aufführst, keine Bedeutung haben. Das ist dein Fall ${\tilde {z}}(t)=e^{j\omega t}$.

Du erklärst hier mit großem Aufwand, wann es einmal einen Unterschied zwischen Winkel und Phasenwinkel geben kann. Im Artikel versuchst du, den Unterschied mit wenigen Zeilen darzustellen. In dieser Kürze kann das überhaupt nicht verstanden werden; ich sehe auch keinen Bezug zwischen deiner Artikel-Einfügung und deiner Darstellung oben.

Ferner schreibst du oben: „für den Spezialfall a=b gilt: α=ωt.“ Da der Spzialfall vorliegt, ist es obendrein völlig müßig, sich mit dem Unterschied an dieser Stelle zu befassen. Der Unterschied zwischen Winkel und Phasenwinkel gehört an eine Stelle, wo das wirklich gebraucht wird, also in einen Spezialartikel. Denk daran, was du oben schreibst: „Und bei ${\tilde {z}}$ gibt der Wert ωt auch tatsächlich einen Winkel an.“

Auf meine Hinweise auf deine mehrfach fehlerhafte Darstellung im Artikel bist du nicht eingegangen.--Saure 17:24, 12. Okt. 2011 (CEST)

Ich erkläre hier mit großem Aufwand, dass Phasenwinkel und echter Winkel zwei verschiedene Sachen sind. Und ich erkläre hier mit großem Aufwand, warum der Phasenwinkel bei einer Schwingung eben kein echter Winkel ist. Ich habe die elliptische Rotation genommen, weil diese anschaulicher ist. Denn bei der elliptischen Rotation gibt es tatsächlich einen echten Winkel und einen Phasenwinkel. Bei der Schwingung gibt es dagegen nur einen Phasenwinkel. Den echten Winkel gibt es bei Schwingungen nur im Spezialfall des Pendels. Und den habe ich im Artikel behandelt.

Und nochmal: Dass α und ωt den gleichen Wert haben, bedeutet noch lange nicht, dass sie die gleiche Sache sind. Es sind zwei komplett verschiedene Sachen, die nur die gleiche Dimension besitzen. Und die im Fall einer Kreisrotation (keiner Schwingung) den gleichen Wert haben. Bei einer Schwingung muss α nichtmal existieren. α existiert bei Schwingungen nur, wenn wir ein Pendel haben.

Und dass dieser Artikel nur den Spezialfall der harmonischen Schwingung betrachtet und nicht Schwingungen allgemein, ist ein Fehler des Artikel. Der Name des Artikels lautet nicht "Phase (harmonische Schwingung)" sondern "Phase (Schwingung)". Also sollte der Artikel alle Formen von Schwingungen beinhalten.

Ansonsten empfehle ich dir noch die Diskussion damals, als der Artikel Kreisfrequenz vom Artikel Winkelgeschwindigkeit getrennt wurde. Der Unterschied zwischen beiden ist nunmal, dass Kreisfrequenz die zeitliche Ableitung der Phase ist, während Winkelgeschwindigkeit die zeitliche Ableitung des Winkels ist. Und da Phase und Winkel zwei verschiedene Sachen sind, gehörte beides in einen unterschiedlichen Artikel. Und auch bei der harmonischen Schwingung eines Pendels kommt es regelmäßig zu Verständnisproblemen, wenn man die Phase des Pendels mit dem Winkel des Pendels verwechselt.

In der Elektronik ist das nicht weiter wichtig. Wenn man Wechselspannung betrachtet, gibt es keinen Winkel. Daher kann man hier ohne Probleme von Winkel sprechen und jeder weiß, dass in Wirklichkeit die Phase gemein ist. Sobald man aber die Schwingung eines Pendels betrachtet, führt es zu Problemen, wenn man von Winkel spricht, aber die Phase meint.

Wo bin ich nicht auf deine Hinweise bzgl. der fehlerhaften Darstellung eingegangen? Meinst du "Beziehung zwischen den Strahlen"? Nun, wenn man wissen will, welche Beziehung gemeint ist, kann man in Artikel Winkel nachschauen. Wenn man jedoch nur den Unterschied wissen will, reicht es vollkommen aus, dass das eine eine Beziehung zwischen zwei Strahlen ist und das andere nicht. Aber von mir aus können wir auch schreiben:

Ein Winkel ist ein Teil der Ebene, der von zwei in der Ebene liegenden Strahlen (Halbgeraden) mit gemeinsamem Anfangspunkt begrenzt wird.

--Eulenspiegel1 20:16, 12. Okt. 2011 (CEST)

„Da Phase und Winkel zwei verschiedene Sachen sind, gehörte beides in einen unterschiedlichen Artikel.“ Den Unterschied allerdings in diesem Artikel zu behandeln, halte ich für falsch, einfach weil es den Rahmen sprengt. Der Artikel wendet sich vorrangig an Elektrotechniker, und „in der Elektronik ist das nicht weiter wichtig.“ Mein Vorschlag: Ich entferne das Wort Winkel komplett aus dem Artikel, und du fügst einen Link ein, unter dem der Unterschied zwischen Phase und Winkel dargelegst wird (beispielsweise beim Pendel, wenn es dort regelmäßig zu Verständigungsproblemen kommt). --Saure 10:45, 13. Okt. 2011 (CEST)

In Ordnung. --Eulenspiegel1 09:10, 14. Okt. 2011 (CEST)

Erledigt. --Saure 09:43, 18. Okt. 2011 (CEST)

Toll! Geschrieben von Fachidioten für Fachidioten! Die Zeit hättet ihr K**gsch****er euch auch sparen können. (nicht signierter Beitrag von 84.131.16.198 (Diskussion) 22:32, 14. Jun. 2013 (CEST))

Die Diskussion "was ist ein Winkel" ist ja so was von daneben... Mal physikalisch: Darf man zur Erdbeschleunigung/Ortsfaktor was auch immer "Fallbeschleunigung" sagen, ja oder nein? Ja, denn sie hat die gleiche Dimension m/(s*s) wie die momentane Geschwindigkeitsänderung (Größenfanatiker), nein, denn keiner auf Erden beschleunigt normalerweise so (Reibung, Erbsenzähler), nein, denn sie ist NICHTT die zweite Ableitung der Geschwindigkeit nach der Zeit, sondern der negative Gradient des planetaren Gravitationspotentialfeldes, etwas einfacher ausgedrückt: Gehört zum Störglied der Bewegungsgleichung und nicht zu dieser Differentialgleichung, außerdem muss man sie dann vielleicht eines Tages umbenennen, wenn sich herausstellt, das träge nicht proportional schwere Masse ist (humpf, das sagt der Theoretiker). Wer hat recht? Alle drei, aber keiner von ihnen entscheidet für WP, da die Wörter auf -beschleunigung eben im Fachsprachgebrauch SIND (also LITERATUR und nicht RUMPHILOSOPHIEREN). Ist der Blindwiderstand ein (ohmscher) Widerstand? Nein, natürlich nicht! Er heißt so, weil er im SI-System die gleiche Einheit hat. Schlagen die WPianer jetze alle tot, die trotzdem noch von ...widerstand reden? Was ist ein Punkt (außerhalb der europäischen Grammatik)? Was ist eine Gerade (Geodäte, dass was ich nach Kneipenbesuch NICHT mehr entlanglaufe,....)? Erfinden kann man viel, aber es gibt unterschiedliche Sprachgebräuche und der von Winkeln ist in Physik und Technik recht klar normiert: Eine DIMENSIONSLOSE Größe (soviel zu Verhältnissen), die in GEWISSEN Fällen in der Einheit rad hilfsweise (Alt-)grad, das kommische Ding mit der 90° dabei, angegeben werden kann. Mathematisch spricht wohl nix dagegen auch das "Argument" einer komplexen Zahl in rad anzugeben. Dann muss halt auch die Exponentialfunkion lernen rad zu verarbeiten. Ich bin sicher, DIE kann das! Kap-lar --84.161.176.54 10:47, 14. Aug. 2013 (CEST)

Phasenverschiebungswinkel

1. Der Begriff Phasendifferenz ist ein der Normung nicht definierter Begriff und sollte unterbleiben, solange es einen genormten Begriff in diesem Sinn gibt.
2. Der Fettdruck des Begriffs Phasendifferenz ist unzulässig.
3. Die vorgenenommene Fallunterscheidung ist unsinnig, da alles ein gemeinsamer Fall ist. Es handelt sich insgesamt um zwei gleichfrequente sinusförmige Schwingungen. --der Saure 17:55, 8. Aug. 2013 (CEST)

zu 1): Es gibt Begriffe außerhalb der Ingenieurwissenschaften, die nicht in den DIN- und ISO-Normen zu finden sind, und trotzdem haben sie ihre Berechtigung. Dies ist kein ingenieurwissenschaftliches Tabellenbuch, sondern eine allgemeine Enzyklopädie. "Phasendifferenz" ist ein sehr wohl und häufig verwendeter Begriff.

zu 2): Ob Fettdruck oder nicht, ist nicht so entscheidend. Da aber der Phasenverschiebungswinkel ein Spezialfall der Phasendifferenz ist, sollte für den Überbegriff auch Fettdruck erlaubt sein, wenn er für den Spezialfall verwendet wird.

zu 3): Vermutlich meinst Du mit Fallunterscheidung den Unterschied zwischen "Phasendifferenz" und "Phasenverschiebungswinkel". Ich kenne den Begriff Phasenverschiebungswinkel nur für den Fall von Stromstärke und Spannung im Wechselstromkreis. Bei der Superposition von zwei Wellen, bei erzwungenen mechanischen Schwingungen oder bei gekoppelten Pendeln würde man vermutlich eher Phasendifferenz sagen. Ich habe den Verdacht, dass Dir die Vielzahl dieser Bedeutungen nicht so ganz bewusst war.

--Pyrrhocorax (Diskussion) 18:22, 8. Aug. 2013 (CEST)

Zu 1) DIN 1311 „legt Begriffe zu Schwingungen und schwingungsfähigen Systemen vorwiegend im Bereich der Mechanik fest. Im Einzelfall werden Hinweise zu analogen Begriffsbestimmungen in der Akustik und Elektrotechnik gegeben.“ Die hier getroffene Sprachregelung ist damit nicht auf Ingenieurwissenschaften beschränkt, schon gar nicht auf Wechselstrom. Aufgabe der Normung ist es unter anderem, einen Wildwuchs von Begriffen einzuschränken. Diese Grundlagennorm führt den Begriff "Phasendifferenz" nicht, sondern in dem Zusammenhang nur den "Phasenverschiebungswinkel" zweier harmonischer Schwingungen $x_{1}(t)$ und $x_{2}(t)$. "Phasendifferenz" ist ein zwar zusätzlich verwendeter Begriff, aber der ist nicht erforderlich, weil es den (einzig) allgemeinverbindlich festgelegten "Phasenverschiebungswinkel" gibt. Die anderen im Artikel zitierten, mehr elektrotechnisch orientierten Normen stimmen zur Begriffsbildung mit der mechanisch orientierten Norm völlig überein.

Zu 2) Die WP-Regelungen zum Fettdruck sehen keine Ausnahmeregelung vor, dass für einen „Überbegriff“ auch Fettdruck erlaubt sein sollte. Alles, was du dazu oben schreibst, ist nichts anderes als persönliche Meinung.

Zu 3) Die von dir postulierte Fallunterscheidung zwischen "Phasendifferenz" und "Phasenverschiebungswinkel" gibt es nicht, einfach weil es den von dir postulierten Begriff in der offiziellen Quelle gar nicht gibt. Dein Eingeständnis „Ich kenne den Begriff Phasenverschiebungswinkel nur für den Fall von Stromstärke und Spannung im Wechselstromkreis“ nährt meinen Verdacht, dass Dir einige „Bedeutungen nicht so ganz bewusst“ sind. Ich habe das Beispiel zum Formelzeichen der elektrotechnisch orientierten DIN 40110 entnommen, weil der Phasenverschiebungswinkel in diesem Kontext häufig verwendet wird. Ich hätte genauso gut, nur etwas abstrakter, aus DIN 1311 den Phasenverschiebungswinkel übernehmen können als $\Delta \varphi =\varphi _{02}-\varphi _{01}$. --der Saure 13:52, 9. Aug. 2013 (CEST)

Ich höre zwischen den Zeilen einen etwas gereizten Unterton. Es war nicht meine Absicht Dich zu reizen, also ganz ruhig: Vielleicht wird ja was Sinnvolles draus, wenn wir nicht nur am gleichen Strang, sondern auch in die gleiche Richtung ziehen ;-) Mein fachlicher Hintergrund ist ein Physikstudium, indem der fragliche Begriff praktisch immer "Phasendifferenz" oder "Phasenunterschied" hieß. Der "Phasenverschiebungswinkel" kam in meiner Erinnerung überhaupt nie vor. Ich kenne ihn nur aus Wikipedia-Artikeln über Elektrotechnik und schloss daraus (so wie es aussieht irrtümlich), dass dieser Begriff auf die Bedeutung in der Wechselstromlehre beschränkt ist. Wenn "Phasendifferenz" und "Phasenverschiebungswinkel" synonym sind, dann ändert das aber nichts daran, dass beide Begriffe fallen sollten, denn (Norm hin, Norm her) in der Physik ist der Terminus "Phasenverschiebungswinkel" ziemlich ungebräuchlich. Für den Abschnitt in dem Artikel bedeutet das, dass eine klare Trennung (nicht im Sinne einer Fallunterscheidung) zwischen dem Allgemeinfall und dem Spezialfall (oder dem Anwendungsbespiel) dringend erforderlich ist, denn mein Missverständnis zeigt ja gerade, dass die Formulierung vor meinem Edit missverständlich war. Ich mache mich gleich an eine Verbesserung des entsprechenden Abschnitts. Zum Thema Fettdruck: Wo finde ich die entsprechende Richtlinie? --Pyrrhocorax (Diskussion) 14:34, 9. Aug. 2013 (CEST)

Wenn erst einmal der eine Begriff definiert worden ist (und der andere nicht), dann sollte man den Undefinierten auch nicht mehr verwenden. Wer erst einmal zu diesem Artikel gefunden hat, braucht nur noch den "richtigen" Begriff, und die Nennung des "falschen" bringt keinen Nutzen. Selbst wenn die Begriffe synonym wären (das brauchen wir jetzt nicht zu diskutieren), gibt es keinen Allgemeinfall und keinen Spezialfall. Das Anwendungsbeispiel betrifft ausschließlich das Formelzeichen. Wenn dieses Beispiel ohne deine Fallunterscheidung ans Ende kommt, habe ich nichts dagegen. Die Formulierung würde besser auf der Diskussionsseite als im Artikel besprochen. Die Regelung zum Fettdruck erfordert eine gewisse Zeit zum Suchen. --der Saure 16:54, 9. Aug. 2013 (CEST)

Keiner der Begriffe ist "falsch" oder "richtig". Der eine ist eben normkonform, der andere nicht. Ich habe spaßeshalber mal die beiden Begriffe über Google Books gesucht. Für "Phasenverschiebungswinkel" erhalte ich 5380 Treffer. Das erste Physik-Buch ("Physik in Formeln und Tabellen" von Berber, Kacher und Langer) wird als 94. Treffer (!) angezeigt, davor ausschließlich technische Literatur. Für "Phasendifferenz" bekomme ich über 59.000 Treffer. Das erste (zudem sehr namhafte) Physik-Buch ist der Pohl an zweiter Stelle. Phasenunterschied hat 26.000 Treffer, Phasenverschiebung 177.000 Treffer. Ausgerechnet der normkonforme Begriff taucht mit Abstand am seltensten auf. Damit will ich nicht sagen, dass die anderen Begriffe besser sind als der Phasenverschiebungswinkel. Aber die Norm ist nicht immer alles. Mein Hobby ist Gleitschirmfliegen, das von Laien gerne mit Drachenfliegen verwechselt wird. Der Gesetzgeber nennt die beiden Fluggeräte "Gleitsegel" und "Hängegleiter". Niemand käme auf die Idee, die beiden Dinge so zu nennen - bloß weil es in irgendwelchen Gesetzen steht. Damit haben die gebräuchlichen Begriffe in der Wikipedia ihre Daseinsberechtigung. Ob man sie fett druckt oder nicht ist dann letztendlich zweitrangig. (Trotzdem interessiert mich die Richtlinie dazu. Ich habe keine gefunden.)

Was hältst Du von dem Abschnitt zum Phasenverschiebungswinkel in der jetzigen Form? Ich habe die Unterscheidung zwischen Phasenverschiebungswinkel und Phasendifferenz herausgenommen (ich glaube, das war Dein Hauptpunkt). Ich habe das Anwendungsbeispiel der Elektrotechnik hinten angestellt (da warst Du ausdrücklich einverstanden). Und ich habe die synonymen, wenn auch nicht normkonformen Termini (Phasendifferenz, Phasenverschiebung, Phasenunterschied) in die Definition aufgenommen. Ich bin ausdrücklich dagegen, auf eine Nennung und Verwendung dieser Begriffe zu verzichten. Ich bin nicht ganz so glücklich mit der Formulierung "Daran gekoppelt ..." (die ich sehr schwülstig finde) und die Einrückung mit Bullet-Point (die ich bei einem Aufzählungspunkt für überflüssig halte). Das könnte man dann ausmerzen, wenn wir uns zumindestens über den Inhalt einig sind. Außerdem finde ich, dass sich der Text etwas gestelzt um die Formel $\Delta \varphi =\varphi _{2}-\varphi _{1}$ drückt. Vielleicht wäre es auch nicht schlecht, wenn man erklären könnte, warum es egal ist, ob man die Differenz der Phasen oder der Nullphasenwinkel nimmt.--Pyrrhocorax (Diskussion) 17:55, 9. Aug. 2013 (CEST)

Habe gerade Deine letzten Änderungen gesehen. Nun bin ich es, der etwas griffelspitzerischer ist: Bist Du Dir sicher und kannst Du eventuell mit den Normen auch begründen, dass der Phasenverschiebungswinkel im allgemeinen Fall tatäschlich mit $\varphi$ statt mit $\Delta \varphi$ bezeichnet werden darf? In der Physik würde man das unter keinen Umständen tun! Im Spezialfall Wechselstromlehre kann man das so machen, weil man ohne Beschränkung der Allgemeinheit $\varphi _{u0}$ oder $\varphi _{i0}$ gleich Null setzen darf. Das geht aber bei beliebigen Schwingungen nicht.--Pyrrhocorax (Diskussion) 20:19, 9. Aug. 2013 (CEST)

Ganz klar ist, dass $\varphi (t)$ und $\varphi$ nicht nebeneinander verwendet werden dürfen. Da du mich danach fragst, habe ich in DIN 1304 "Formelzeichen" nachgeschlagen. Unmittelbar untereinander stehen

$\varphi (t)$ für Phasenwinkel,

$\varphi$     für Phasenverschiebungswinkel.

Bei einem periodischen Vorgang gibt es keinen herausragenden Zeitpunkt für die Festlegung des Nullpunktes. Denk an die Definition des Mittelwertes einer periodischen Funktion; die Wahl des Integralanfangs ist ausschließlich eine Frage der Zweckmäßigkeit! Ich weiß nicht, von welchen „beliebigen Schwingungen“ du redest. Dieser Artikel beschränkt sich ausdrücklich auf Sinus-Schwingungen. Da ist es eben wichtig, die Definition der Phase als Argument der Winkelfunktion im Auge zu behalten, was bei einem Oberschwingungsgehalt nicht mehr geht (oder nur für die Grundschwingung, deren Nulldurchgang nicht notwendig mit dem Nulldurchgang der Gesamtfunktion übereinstimmt).

Zu „In der Physik würde man das unter keinen Umständen tun!“ habe ich gerade bei Pohl gefunden (S: 129) $I=I_{0}\sin(\omega t-\varphi )$. So sehr ich den Pohl einerseits schätze (ich bin auch Physiker), ich gehe zunehmend auf Abstand wegen seiner schlampigen Verwendung der Begriffe.

Zu einer früher gestellten Frage: Siehe WP:TYP#Schriftauszeichnung. --der Saure 11:11, 10. Aug. 2013 (CEST)

Zu Deinem letzten Punkt zuerst: Danke für die Mühe! Wenn ich diese Richtlinie aber wörtlich nehme, dann darf der Fettdruck nur für das Lemma (bzw. Synonyme, wenn es Weiterleitungen für sie gibt) verwendet werden. Das würde bedeuten, dass weder Phasenverschiebungswinkel noch Phasendifferenz fett gedruckt werden dürfen. Ob Norm oder nicht, ist dafür vollkommen irrelevant.

Den Punkt davor verstehe ich nicht: Die aus Pohl zitierte Gleichung enthält doch gar keine Phasendifferenz von zwei Schwingungen. Das dort auftauchende $\varphi$ hat die Bedeutung von $\varphi _{0}$ in diesem Artikel, nicht die Bedeutung von $\Delta \varphi$. Mir war es wichtig, dass Differenzen von Größen auch als solche kenntlich gemacht werden. Die Differenz von zwei Größen ist nur dann mit einer absoluten Größe gleich, wenn die andere Null ist. Wie gesagt: Bei Wechselströmen und -Spannungen kann man einen der Nullphasenwinkel willkürlich gleich Null setzen. Im allgemeinen Fall darf man das nicht tun. Und mit allgemein meine ich z. B. gedämpfte Schwingungen. Deswegen hätte ich nichts dagegen, den Phasenverschiebungswinkel $\varphi _{ui}$ ohne Delta zu schreiben, würde diese Schreibweise aber nicht ohne Not auf andere Phasenverschiebungen ausdehnen. --Pyrrhocorax (Diskussion) 23:13, 11. Aug. 2013 (CEST)

Zu Absatz 1: Der Weiterleitungsname Phasenverschiebungswinkel führt über eine (zwischenzeitlich hinzugekommene) Verzweigung zum Zielartikel. Phasendifferenz steht nicht in Fettdruck. Wo ist dein Problem? (Rhetorische Frage)

Zu Absatz 2:

1. Eine als Differenz definierte Größe muss nicht nochmal im Formelzeichen als Differenz gekennzeichnet werden.
2. Die Frage, ob „der Phasenverschiebungswinkel im allgemeinen Fall tatäschlich mit $\varphi$ statt mit $\Delta \varphi$ bezeichnet werden darf“, hatte ich dir bereits oben beantwortet – einschließlich des erbetenen Norm-Belegs.
3. „Bei Wechselströmen und -Spannungen kann man einen der Nullphasenwinkel willkürlich gleich Null setzen. Im allgemeinen Fall darf man das nicht tun.“ Wieso denn; gilt in der Elektrotechnik eine andere Mathematik als im allgemeinen Fall? (Rhetorische Frage, denn die Beliebigkeit des Nullpunktes bei einem periodischen Verlauf hatten wir auch schon!)
4. Gedämpfte Schwingungen sind keine harmonischen Schwingungen. Thema verfehlt.
5. Nachdem im Pohl der Nullphasenwinkel der Spannung zu null gesetzt worden ist, ist unklar, ob es sich bei dem $\varphi$ um ein $\varphi _{I}$ oder ein $\varphi _{UI}$ handelt (abgesehen von Vorzeichen, aber da macht in diesem Zusmmenhang sowieso jeder, was er will). --der Saure 11:49, 12. Aug. 2013 (CEST)

Zu Absatz 1: Das mit der Weiterleitung wusste ich nicht. Allerdings finde ich die Weiterleitung auf diesen Artikel falsch. Vielmehr sollte die Weiterleitung nach Phasenverschiebung erfolgen. Zu Deiner rhetorischen Frage: Mir kam es bisher so vor als würdest Du den Fettdruck für Phasenverschiebungswinkel damit begründen, dass er normkonform wäre, Phasendifferenz aber nicht. Daraus entwickelte sich die Diskussion und meine Frage nach den Richtlinien für Fettdruck. Wenn der Fettdruck über die Weiterleitung begründed wird, ist das natürlich was anderes. Nichtsdestotrotz halte ich die Weiterleitung für falsch.

Zu Absatz 2:

1. Sollte sie aber! $\Delta t$ ist was anderes als $t$. Das eine ist eine Zeitdauer, das andere ein Zeitpunkt. Genauso verhält es sich mit der Phase auch.
2. ... und ich habe Dir auch schon gesagt, dass die Norm nicht alles ist. In den Physikbüchern, die ich kenne, werden Differenzen mit Delta geschrieben. Da beißt die Maus keinen Faden ab.
3. (siehe nächster Punkt)
4. Von wegen Thema verfehlt! Es geht hier um den Begriff der Phase. Natürlich hat dieser Begriff auch bei gedämpften Schwingungen eine Bedeutung. Dass dies keine harmonischen Schwingungen im eigentlichen Sinne sind, ist mir klar. Deswegen beharre ich ja in der ganzen Diskussion darauf, dass nicht geschrieben werden darf, was für die streng harmonischen Schwingungen gilt. Was für Wechselströme richtig und sinnvoll ist, lässt sich nicht komplett auf andere Probleme (in diesem Beispiel: Gedämpfte Schwingungen) übertragen.
5. Ja. Hatte ich nicht genau das gesagt? Zitat: Die aus Pohl zitierte Gleichung enthält doch gar keine Phasendifferenz von zwei Schwingungen. Das dort auftauchende $\varphi$ hat die Bedeutung von $\varphi _{0}$ in diesem Artikel, nicht die Bedeutung von $\Delta \varphi$. Phasendifferenzen treten auf, wenn man zwei Schwingungen betrachtet. Hier ist nur von einer die Rede. Folglich ist das auftauchende $\varphi$ auch keine Differenz, sondern es ist der Nullphasenwinkel der Stromstärke.--Pyrrhocorax (Diskussion) 12:45, 12. Aug. 2013 (CEST)

Schade, dass es dir so schwer fällt, genau zu lesen. Phasenverschiebungswinkel ist als Differenz definiert, ganz im Gegensatz zur Zeit; dein Vergleich ist unpassend. Die vielen Spezialisten, die einen Normungsausschuss bilden, und die Vielen, die gegen einen Normentwurf Einspruch erheben können, denken zusammen wahrscheinlich etwas weiter als ein einzelner Universal-Lehrbuchverfasser. Eine Periodendauer bezeichnest du wohl kaum mit ΔT, einfach weil sie als Zeitdifferenz definiert ist. Für die gebildete Differenz einer fortlaufenden Größe ist selbstverständlich ein Δ angebracht. In unserem Artikel ist es etwas schwierig, weil der Phasenverschiebungswinkel als Differenz zweier Größen definiert ist, die ebenfalls mit φ bezeichnet werden. Deshelb hat Δφ einen Sinn, aber deinem Anspruch, nur Δφ mache Sinn, schließen sich die Normschreiber nicht an. Und ich vertrete keine eigene Meinung, sondern halte mich an die Institution, die dazu berufen ist, Verbindliches festzulegen.

Die Unterscheidung in harmonischen Schwingungen und harmonischen Schwingungen im eigentlichen Sinne kann ich nicht nachvollziehen. Alle vier Normen, die mir zum Thema zugänglich sind, definieren den Phasenwinkel ausschließlich im Falle der harmonischen Schwingung. Selbstverständlich kannst du dir deine Begriffe anders definieren, dann sprechen wir aber keine gemeinsame Sprache mehr, und jede weitere Diskussion ist sinnlos.

Den Artikel Phasenverschiebung halte ich für ausgesprochen schlecht, so dass ich eine Verlinkung dorthin nicht verantworten kann. Nur so nebenbei – nicht als Begründung zum vorstehenden Satz – verwendet der Artikel für den Phasenverschiebungswinkel sowohl φ als auch Δφ, allerdings ohne zu schreiben, dass beide Formelzeichen dieselbe Größe meinen. --der Saure 18:04, 12. Aug. 2013 (CEST)

Naja, der Vergleich mit der Periodendauer hinkt ein wenig. Zwar gebe ich Dir recht, dass hier auch für eine Zeitspanne ein Formelzeichen ohne Delta verwendet wird. Aber $T$ wird auch nicht als die Differenz von zwei verschiedenen $T$s definiert. Verstehst Du was ich meine? Es ist einfach unschön, für eine Größe und für deren Änderung dasselbe Formelzeichen verwenden. Deswegen wird ein Autor, wenn er verständlich bleiben will, auf das Delta nicht verzichten. Er wird nur dann $\varphi$ ohne Delta für die Phasenverschiebung schreiben, wenn nirgends der Momentanwert der Phase auftaucht. Dieser Artikel dreht sich aber um den Momentanwert der Phase.

Zu den harmonischen und gedämpften Schwingungen: Sagen die von Dir so geschätzten Normen zu der Bedeutung von $\varphi (t)$ in gedämpften Schwingungen oder nicht? Wenn ja: Wie heißt diese Größe dann dort: Phase(nwinkel) oder anders? Wenn nein: Dann sind die Normen in diesem Punkt nicht vollständig. Wikipedia bildet das gesamte Wissen ab, nicht nur der Teil, der in Normen Einzug gefunden hat.

Zu dem Artikel Phasenverschiebung: Ich finde ihn nicht so schlecht wie Du. Was findest Du so schlimm daran? Gerade das, was von Dir so sehr bemängelt wird – Zitat: ... verwendet der Artikel für den Phasenverschiebungswinkel sowohl φ als auch Δφ, allerdings ohne zu schreiben, dass beide Formelzeichen dieselbe Größe meinen – stimmt nicht. Dort steht: ... und die Phasenverschiebung als Winkel Δφ oder (wenn Verwechslungen ausgeschlossen sind) als φ angegeben. (Außerdem wird praktisch durchgängig Δφ geschrieben - mit ganz wenigen begründeten Ausnahmen).--Pyrrhocorax (Diskussion) 18:53, 12. Aug. 2013 (CEST)

Immer wieder dein unsauberes Lesen und Schreiben: Was ich oben ausdrücklich nicht als Kritik geschrieben habe, zitierst du als „was von Dir so sehr bemängelt wird“. So hat eine Diskussion keinen Zweck.

Wenn du den Artikel Phasenverschiebung nicht so schlecht findest, dann stelle doch dort deine persönlichen Vorstellungen ein. Ich habe meine Mitwirkung an diesem Artikel lange eingestellt und werde ihn auch weiterhin nicht beobachten.

Die Normung behandelt auch gedämpfte Schwingungen, aber den Phasenwinkel definiert sie an ungedämpften Schwingungen. Die von mir „so geschätzten Normen“ sagen „zu der Bedeutung von $\varphi (t)$ in gedämpften Schwingungen“ nichts. Allein schon mit dieser Frage postulierst du, dass es überhaupt eine Bedeutung gibt. Jeden Versuch, hier eine Extrapolation vorzunehmen, sehe ich als persönliche Meinung an, die bei WP nichts zu suchen hat. Ob die Frage: „Wie heißt diese Größe dann dort“? irgend jemanden interessiert, ob die Frage überhaupt einen Sinn hat, und wenn ja, ob die Frage jemals beantwortet worden ist, bleibt offen. Vielleicht ein Thema für deinen Nobelpreis? Auch mit deinen „Wikipedia bildet das gesamte Wissen ab“ ohne jede Abgrenzung in Blick auf Relevanz, erhebst du einen Vollständigkeitsanspruch, über den ich nur lächeln kann.

Jedenfalls werde ich mich beim Artikel Phasenwinkel weiterhin dafür einsetzen, dass dieser wesentliche Festlegungen der Fachleute korrekt wiedergibt und darüberhinaus von persönlichen Vorstellungen frei bleibt. --der Saure 12:08, 13. Aug. 2013 (CEST)

Einmal darüber geschlafen und schon sieht die Welt ganz anders aus: Lass uns mal sachlich bleiben. Anlass für diese nun schon recht längliche und (da sind wir uns sicher einig) fruchtlose Diskussion war Dein Edit, demzufolge die Phasendifferenz bzw. der Phasenverschiebungswinkel neben $\Delta \varphi$ auch mit $\varphi$ bezeichnet werde. Das hatte ich kritisiert. Meine Begründung war, dass Differenzen mit Delta geschrieben werden, um deutlich zu machen, dass es sich nicht um Momentanwerte handele. Dieser Artikel handelt prinzipiell nicht von der Differenz (das ist nur eine Randnotiz) sondern ganz überwiegend von dem Momentanwert. Die Gefahr einer Verwechslung liegt also auf der Hand. Das war der Ausgangspunkt und darum sollte es eigentlich gehen. (Der Nebenkriegsschauplatz "gedämpfte Schwingungen" hat prinzipiell wenig mit der eigentlichen Frage zu tun. Legen wir ihn einfach beiseite. Es darf jeder seine Meinung dazu haben, wer von uns beiden nun rechthaberischer war.) Dazu werde ich gleich eine kleine Ergänzung in den Artikel einfügen. Wenn Du daran nichts auszusetzen hast, sind wir dann beide mit dem Text einig. Zwar haben wir dann nach wie vor unterschiedliche Meinungen zu der Frage, ob $\omega t+\varphi _{0}$ auch bei gedämpften Schwingungen „Phase“ genannt werden darf. Aber das ist für den Artikel ohne Belang. Beste Grüße - ganz ohne Gram --Pyrrhocorax (Diskussion) 13:19, 13. Aug. 2013 (CEST)

Nachtrag: Es mag ja sein, dass Du den Artikel Phasenverschiebung nicht toll findest. Ob Du an einer Verbesserung des Artikels mitarbeiten möchtest oder nicht, bleibt natürlich Dir überlassen. Wenn aber hier in diesem Artikel das Wort Phasenverschiebung verwendet wird und wenn es einen Artikel mit diesem Lemma gibt, dann ist ein Wikilink auf jenen Artikel dringend angezeigt, also lass ihn bitte im Artikel drin. --Pyrrhocorax (Diskussion) 17:06, 13. Aug. 2013 (CEST)

Bessere Quellen und besserer Lemmatitel.

1. Die einzigen Quellen sind 4 Fußnoten, die auf DIN-Normen verweisen (führe ich weiter unten aus)
2. Die erste DIN-Norm ist einschlägig, dort wird das, was das Lemma beschreiben will, nämlich den Momentan"winkel" eines Zeigers im Kreisdiagramm einer harmonischen Schwingung bzw. das Argument omega*t in einer trigonometrischen Funktion, die die Schwingung beschreibt, ganz eindeutig als Phasenwinkel bezeichnet. Das ist meines Erachtens auch ein weniger missverständlicher Ausdruck.

In dem offiziösen Dokument zur Norm DIN 1311-1 (als Erste Fußnote im Artikel verlinkt) hier (PDF) wird genau das, was der Artikel beschreibt als Phasenwinkel definiert (DIN 1311-1; 5.11.6 in dem Dokument auf Seite 4). In der zweiten Fußnotennorm geht es offenbar um Schriftsatz (welche Zeichensätze für welche Größen angemessen sind, wie breit Bruchstriche sein dürfen usw.... tja in Deutschland bleibt nix ungeregelt). In der dritten Fußnote DIN 40108 geht es ausweislich von denen "IG-EVU Interessengemeinschaft Energieverteilung (PDF) um "Elektrische Energietechnik, Stromsysteme - Begriffe, Größen, Formelzeichen". Näheres zu erfahren kostet laut der ersten 15 google-Funde Geld - naja es geht um Strom. Aber wohl sehr viel spezieller, als was dieser Artikel "Phase einer Schwingung" beschreiben will. In der Norm der vierten Fußnote geht es anscheinend um die Messung der Blindleistung.

Vorschlag: Tut uns Lehrern einen Gefallen, und nennt das Lemma nach DIN 1311-1 5.11.6 Phasenwinkel, denn in der Redundanz liegt der Tanz:

• Das Wort gibt einen Zaunlattenhinweis darauf, welche Einheit für die Größe in Frage kommen. Zum Beispiel NICHT Sekunde, Jahrhundert ("in der Phase des Wiederaufbaus des Haumichtoter Domturms..."), was alles zu dem außertechnischen Sprachgebrauch eher passt als die Bedeutung phi in phi=omega*t, vom Cosinus einer Schwingung.
• Mein Elektriker denkt vielleicht in 20 Jahren nicht mehr, wenn ich Phase sage, dass ich gleich in eine Steckdose greifen will und wenn er es sagt und Phasenwinkel meint, und ich ihn nicht versteh, dass ich halt auch sone Trottel bin.

Und Literaturhinweise, die nix kosten, sind immer auch eine gute Beigabe zu einem Artikel. Danke! --KleinKlio (Diskussion) 11:08, 13. Aug. 2013 (CEST)

Ich sehe grad erst im Nachhinein, dass mein 2. Punkt bereits im weiter oben von Benutzer:Saure (im Wesentlichen) gebracht wurde. Also: In dieser Sache bin ich (verschärft) seiner Meinung. Lieber ein paar Leute ärgern, als Begriffsfindung!--KleinKlio (Diskussion) 11:18, 13. Aug. 2013 (CEST)

Einer Umbenennung in Phasenwinkel spricht meiner Meinung nach nichts entgegen. Im Sprachgebrauch ist trotz Norm der Begriff Phase mindestens ebenso häufig, wenn nicht sogar häufiger, aber dafür gibt es bei Wikipedia den Redirect. Für "Phase" würde sprechen, dass es sich ja nicht um einen Winkel im geometrischen Sinne handelt, aber was soll's? Der Zitronenfalter faltet ja auch keine Zitronen. Ich hätte auch nichts dagegen, die Normen auf eine einzudampfen, wenn diese ausreichend ist, um die Definition, Benennung und Einheit zu belegen. --Pyrrhocorax (Diskussion) 11:26, 13. Aug. 2013 (CEST)

Hallo KleinKlio! Als ich das erste Mal auf diesen Artikel gestoßen bin, habe ich Belege für Phase gesucht, aber nur für Phasenwinkel gefunden. Damals war ich noch unerfahren bei WP und habe mir eine Verschiebung nicht zugetraut. Jetzt hast du sie angestoßen, und so soll es geschehen, wenn kein Einspruch kommt.

Dank für den Link auf den öffentlichen Zugang zu DIN 1311. Er wird eingebaut. DIN 40110 ist eine sehr breit angelegte Norm zu Wechselgrößen, hat mit Messung der Blindleistung fast nichts zu tun. Es gibt bei WP viele Artikel, in denen ich mich auf diese Norm abgestützt habe. DIN 5483 ist ebenfalls sehr viel breiter als du vermutest, vergleichbar eher mit DIN 1311.

Die Verschiebung von "Phase (Schwingung)" nach "Phasenwinkel" werde ich in mehreren Schritten ausführen, weil sowohl "Phasenwinkel" als auch "Phase" als BKS mit beachtet werden müssen. --der Saure 16:10, 13. Aug. 2013 (CEST)

Einspruch.

Im Zusammenhang mit Lasern und in der Quantenoptik ist "Phasenwinkel" eher ungewöhnlich. Das gilt auch ganz allgemein für die Quantenmechanik mit ihren Wellenfunktionen und für die Teilchenphysik vom Standardmodell über die QCD bis zur Stringtheorie. Es betrifft also nicht weniger als den Großteil der modernen Physik. Zu einer Verschiebung auf eine lediglich in der Elektrotechnik übliche Wortwahl besteht kein Anlass.---<)kmk(>- (Diskussion) 00:54, 20. Aug. 2013 (CEST)

Dieser Einspruch steht in Zusammenhang mit lauter Themen, die in dem Artikel überhaupt nicht vorkommen. Deshalb ist der Einspruch ohne jede Relevanz. Im Gegenteil: Für eine in der Elektrotechnik anerkannte übliche Wortwahl ist die Verschiebung auf eben diese Wortwahl geboten.

Falls ein Zusammenhang mit Lasern usw. jemals behandelt wird, müsste dieses in einem anderen Artikel stehen. Dafür steht das durch die Verschiebung frei werdende Lemma zur Verfügung. --der Saure 10:07, 20. Aug. 2013 (CEST)

• Der Artikel behandelt ganz allgemein die Phase einer Schwingung. Und das ist auch gut so. Schwingungen kommen schließlich auch außerhalb der eng bemessenen Domäne der elektrischen Signale vor.
• Interferenz und Superposition sind Themen die sich quer durch die Physik ziehen. Laser, Licht und Quantenmechanik sind ohne sie nicht denkbar. Ebenso sind Phasenverschiebungen und Phasenmodulation Phänomene, die überall vorkommen, wo Schwingungen eine zentrale Rolle spielen. Also insbesondere in der Akkustik, der Quantenoptik und der Quantenmechanik - aber ich wiederhole mich. Wie Du vor diesem Hintergrund zu der Einschätzung kommst, ich hätte nur Themen aufgeführt, die im Artikel nicht vorkommen würden, ist nicht wirklich nachvollziehbar.
• Die von Dir vorgeschlagene inhaltliche Doppelung in einem Artikel mit dem synonymen Lemma "Phasenwinkel" führt zu unerwünschter Redundanz.

---<)kmk(>- (Diskussion) 23:45, 20. Aug. 2013 (CEST)

Bitte, dann definiere doch einmal, was denn „die Phase einer Schwingung“ ist. Wo immer ich nach einer Definition gesucht habe, bin ich immer nur unter Phasenwinkel fündig geworden. Beispielsweise sind auch Phasenverschiebungen und Phasenmodulation nur Veränderungen am Phasenwinkel. --der Saure 09:47, 21. Aug. 2013 (CEST)

Such mal in diesen Lehrbüchern: Gerthsen/Meschede, Stuart/Klages, Otten

Mit "Phasenwinkel" wird übrigens recht häufig das bezeichnt, was die DIN "Nullphasenwinkel" nennt. Zum Beispiel bei Ulrich Harten, Heinz Parkus, D. Giancoli, Hering/Stohrer, Dobrinski/Vogel

Andere Autoren nennen das "Phasenwinkel", was in der DIN ein "Phasenverschiebungswinkel" ist. Dazu gehört unter anderem der Dubbel (Kapitel 4.1.4 "Gedämpfte Schwingungen"), der Rybach, der Pohl

-<)kmk(>- (Diskussion) 02:40, 25. Aug. 2013 (CEST)

Danke für die Mühe! Angesichts dieses Wildwuchses kann man keinem der Verfasser die Funktion eines sprachbildenden Wortführers zuweisen. Gerade zur Vermeidung so vieler unterschiedlicher Einzeldefinitionen ist die Normung etabliert worden. Sie soll „auf den gesicherten Ergebnissen von Wissenschaft, Technik und Erfahrung basieren und auf die Förderung optimaler Vorteile für die Gesellschaft abzielen. Die Festlegungen werden mit Konsens erstellt und von einer anerkannten Institution angenommen.“ „Für die Ausarbeitung wird ein Gremium aus allen betroffenen Fach- und Interessentenkreisen“ einberufen. Also es wird hier keine Einzelmeinung, sondern ein Konsenzergebnis vorgestellt, das auch ein Einspruchsverfahren durchlaufen hat.

Ich stelle mir weiterhin vor, dass zur Begriffsklärung bei WP keine persönliche Meinung, sondern dieses Ergebnis vorgestellt wird, und dass alle anderen von dir genannten Begriffe auf den einzigen Artikel weiterleiten. Ich weiß um deine Abneigung gegen jede Norm, aber du hast ein Musterbeispiel geliefert, wie widersprüchlich Literatur sein kann, wenn die Defintionen individuell sind. Es grüßt --der Saure 10:59, 26. Aug. 2013 (CEST)

PS: Muss die Diskussion, die deinen Redaktionskollegen Pyrrhocorax dazu gebracht hat, der Umbenennung zuzustimmen, jetzt wirklich nochmal geführt werden? --der Saure 11:32, 21. Aug. 2013 (CEST)

Ich finde Phase gut und Phasenwinkel schlecht. --Pediadeep (Diskussion) 22:53, 21. Aug. 2013 (CEST)

Bitte Empfindungen und Traditionen von Argumenten und Festlegungen trennen.

Zur Versachlichung ein Auszug aus DIN 5483-1 Zeitabhängige Größen – Benennungen der Zeitabhängigkeit:

Phasenmodulierter Sinusvorgang: Die Phasenwinkelabweichung Δψ(t) des modulierten vom unmodulierten Sinusvorgang ändert sich zeitlich, proportional zu einem modulierenden Vorgang. --der Saure 10:38, 23. Aug. 2013 (CEST)

das ist eben meine meinung. wikipedia ist nicht der vollstrecker der DIN. --Pediadeep (Diskussion) 19:30, 23. Aug. 2013 (CEST)

Zeiger

@der Saure: Bitte nicht einfach sinnvolle Änderungen revertieren.

1. "Zeiger" ist der Fachbegriff.
2. Es gibt einen Wikipedia-Artikel, wo alles drinsteht, was man darüber wissen muss.
3. Es ist keine "Strecke", die da rotiert. Strecken haben die Dimension von Längen. Das gezeichnete Beispiel hat vermutlich die Dimension einer Spannung.
4. Schau Dir mal die Formulierung in der ursprünglichen Form an und meine Veränderung. Welche ist da verständlicher und vom Satzbau her korrekter?

Du erweckst den Eindruck, als würdest Du jede Änderung an diesem Artikel aus Prinzip blockieren. Bitte geh einfach mal davon aus, dass alle, die sich an der Wikipedia aktiv beteiligen, auch eine Verbesserung anstreben. --Pyrrhocorax (Diskussion) 17:02, 13. Aug. 2013 (CEST)

@Pyrrhocorax: Bitte nicht einfach sinnvolle Textpassagen verschlimmbessern.

Die schier endlose Diskussion zeigt, dass du unentwegt neue, nicht ausreichend überlegte Dinge vorbringst. Wozu bei einem mißverständlichen (bzw. vielfach mißbrauchten) Begriff erst nachlesen in einem „Wikipedia-Artikel, wo alles drinsteht, was man darüber wissen muss“, wenn ohne den Umweg über den Begriff auch alles klar ist? Der Begriff Zeiger wird in seinem Artikel nicht erklärt, nur dass er rotiert und eine Länge hat; seine Natur bleibt offen: anfangs ist er wohl reell, später „eine komplexe Zahl“, also mit der Dimension 1.

Dabei ist es gar nicht erforderlich, für eine harmonische Schwingung auf komplexe Größen zu gehen. Die schlichte anschauliche Strecke im Bild ist völlig ausreichend, egal welche physikalische Größe ${\hat {u}}$ dahinter steckt. Mach dich duch nicht lächerlich mit deiner Dimension Länge. Unter Zeigermodell steht doch für ${\hat {y}}$ auch nur „Länge des Zeigers“, die dann „Amplitude der Schwingung“ bedeutet, mit einer Einheit, die beliebig ist. Was du anstrebst ist das Eine, was du zustande bringst ist etwas Anderes.

Mit deinem Schlusssatz sind wir dann möglicherweise am Kernproblem dieser langen Diskussion: Guter Wille alleine reicht nicht aus. Bei Weitem nicht!! Es gibt auch Schüler und Lehrlinge, die bei WP mit anerkannt gutem Willen ihr Wissen einbringen und „eine Verbesserung anstreben.“ Bloß diese erkennen meistens sehr bald, dass das Anstreben einer Verbesserung alleine nicht reicht. --der Saure 09:46, 14. Aug. 2013 (CEST)

Guter Wille allein reicht nicht. Soso. Kannst Du belegen, dass das rotierende Ding in der Fachliteratur "Strecke" genannt wird? Ich glaube kaum, denn ich habe diesen Begriff noch nie in dem Zusammenhang gehört. Es gibt einen Fachbegriff dafür und der lautet Zeiger bzw. Zeigerdiagramm. Deswegen muss der in diesem Artikel auch genannt werden. Wenn im Artikel Zeigermodell was unscharf oder falsch ist, dann muss das dort verändert werden (habe gerade "komplexe Zahl" durch "komplexe Größe" ersetzt). Das hat nichts mit meinem "guten Willen" zu tun oder damit, dass ich "unentwegt nicht ausreichend überlegte Dinge" vorbringe, sondern so funktioniert die Wikipedia. Genauso verhält es sich mit dem Artikel Phasenverschiebung, dessen Link Du beharrlich aus diesem Artikel rausnimmst. Und kein Wort sagst Du zu meinen anderen Edits. Meine Formulierung ist: Man kann sich eine solche Schwingung durch einen Zeiger veranschaulichen, der sich mit konstanter Winkelgeschwindigkeit um den Koordinatenursprung dreht. Wenn man diesen Zeiger auf eine der beiden Koordinatenachsen projiziert, führt der Endpunkt der Projektion dabei die harmonische Schwingung aus. Du hast das revertiert, weil Du die folgende Formulierung anscheinend besser fandest: Man kann sich solche Schwingungen veranschaulichen mit der Projektion einer Strecke auf die x-Achse, wenn die Strecke sich mit konstanter Winkelgeschwindigkeit um den Koordinatenursprung dreht. Der Endpunkt der Projektion führt dabei die harmonische Schwingung aus. Das ist erstmal stilistisch und grammatikalisch schlecht. Dann ist von einer x-Achse die Rede. (Erstens ist es egal, welche Achse man für die Projektion nimmt. Zweitens: Welche Bedeutung hat hier die Variable x??). Und schließlich ist es didaktisch schlecht, weil es vom Leser verlangt, mehrere Schritte auf einmal mitzudenken. Trotzdem hast Du meine Änderung einfach kassiert, weil Dir ein paar Punkte im Artikel Zeigermodell nicht gefallen. Das wirkt auf mich - mit Verlaub - sehr halsstarrig.

Ich bin fachlichen Argumenten durchaus aufgeschlossen. Deine Begründungen dafür, warum Du die Wikilinks Zeigermodell und Phasenverschiebung nicht im Artikel haben möchtest, waren aber nicht fachlich. Deine anderen Revertierungen hast Du gar nicht begründet.

Weiterhin auf eine gute Zusammenarbeit. --Pyrrhocorax (Diskussion) 10:34, 14. Aug. 2013 (CEST)

Soso. Du kannst nicht umsetzen, dass „das rotierende Ding“ elementar geometrisch eine Strecke ist? Für etwas so Anschauliches willst du Fachliteratur heranziehen? Der Begriff Zeiger ist ein mißverständlicher (bzw. vielfach mißbrauchter) Begriff, hier völlig überflüssig, und das Bemühen einer nicht erklärten, „häufig“ komplexen Größe ist an dieser Stelle nur ein überflüssiger mathematischer Überbau.

Da der Textteil, um den es hier geht, ausschließlich die harmonische Schwingung beschreibt und nichts zum Verständnis des Phasenwinkels beiträgt, ist er völlig überflüssig (die Bildlegende zur Veranschaulichung reicht).

Dann dein neues Argument mit der x-Achse. Sicher ist es egal, welche Achse man nimmt, aber zur Illustration für die im Text vorkommende Kosinusfunktion ist es sinnvoll, genau diese zu nehmen. Zur Vermeidung von Unklarheit ist diese Achse im Bild als solche gekennzeichnet. Deinen guten Willen habe ich bisher nicht angezweifelt, aber bei solchem Einwand …

„Welche Bedeutung hat hier die Variable x??“ Wieder so ein völlig überflüssige Frage, die nichts mit dem Thema zu tun hat. Gegenfrage: Im Artikel Zeigermodell, welche Bedeutung hat denn da die Variable x bei der im Text vorkommenden x-Achse, die im Bild nicht einmal als solche gekennzeichet ist?

Auf die Fülle dessen, was du ständig neu produziert, kann ich wirklich nicht komplett eingehen. (Bleib schön zurückhaltend: Du gehst ja auch auf meine Kritik nicht ein.) Ein bisschen Satzbauänderung ist sicher hinzubekommen, nur ist sie mit dem nichtsnutzigen Begriff Zeiger verbunden. Die Behauptung, die in „mit dem Artikel Phasenverschiebung, dessen Link Du beharrlich aus diesem Artikel rausnimmst“ steckt, ist schlicht und einfach falsch. Aber ich werde die Doppelverlinkung nun an anderer Stelle herausnehmen.

In deinem letzten Diskussionsbeitrag mit dem Gipfel der aberwitzigen Frage nach der Variablen x sehe ich weder ein ein Zeichen guter Zusammenarbeit noch ein Streben nach Verbesserung, noch ein Indiz für etwas, das über dieses Streben hinaus unbedingt erforderlich ist. --der Saure 12:07, 15. Aug. 2013 (CEST)

1. Du schreibst: Du kannst nicht umsetzen, dass „das rotierende Ding“ elementar geometrisch eine Strecke ist? Für etwas so Anschauliches willst du Fachliteratur heranziehen? Warum in Dreiteufelsnamen weigerst Du Dich, für dieses Ding den vernünftigen Fachbegriff zu verwenden? Es heißt Zeiger. Dafür gibt es einen Artikel und so wird es in der Literatur verwendet. Meine (rhetorische) Frage zielt darauf ab, dass in der Literatur dieses Ding eben nicht Strecke genannt wird, sondern Zeiger. Dein nun gewählter Begriff Radius ist ebenso schlecht, denn der Radius ist kein Vektor. Für die Einführung des Phasenwinkels ist aber der Vektorcharakter des Zeigers unerlässlich. Eine Erklärung, warum der Begriff missverständlich sei oder missbraucht werde, bleibst Du schuldig. Was Du hier vertrittst, ist Deine private Meinung und lässt sich nicht durch die Literatur belegen, in der der Begriff Zeigerdiagramm ständig verwendet wird.
2. Du schreibst: Da der Textteil, um den es hier geht, ausschließlich die harmonische Schwingung beschreibt und nichts zum Verständnis des Phasenwinkels beiträgt, ist er völlig überflüssig (die Bildlegende zur Veranschaulichung reicht). Ich halte diesen Textteil für überhaupt nicht überflüssig! Er ist die omA-taugliche Motivation des Begriffs der Phase. Die Abbildung dient der Veranschaulichung des Textes - nicht umgekehrt. In der jetzigen Form hängt die Abbildung ohne Erklärung völlig in der Luft und hat keinen offensichtlich erkennbaren Bezug zum Text.
3. Du schreibst: Dann dein neues Argument mit der x-Achse. Sicher ist es egal, welche Achse man nimmt, aber zur Illustration für die im Text vorkommende Kosinusfunktion ist es sinnvoll, genau diese zu nehmen. Zur Vermeidung von Unklarheit ist diese Achse im Bild als solche gekennzeichnet. Deinen guten Willen habe ich bisher nicht angezweifelt, aber bei solchem Einwand Das war die Begründung, warum der ursprüngliche (von mir geänderte) Text schlecht war. Die verwendete Formulierung erweckte den Eindruck, dass es von Bedeutung sei, dass die Projektion auf die x-Achse erfolgte. Meine Formulierung kam ohne das Wort x-Achse aus und war zudem verständlicher. Nach der Bedeutung der Variable x fragte ich, weil der in der Zeichnung auftauchende Zeiger anscheinend die Dimension einer Spannung hat. Damit haben auch die Koordinatenachsen die Dimension einer Spannung. Richtig wäre also die Achsenbeschriftung Re(u) - was natürlich nur dann einen Sinn macht, wenn man im Komplexen arbeitet. Möglich wäre auch u(t). Deswegen der Einwand. (Im Artikel Zeigermodell sind die Achsenbezeichnungen mit x und y aber korrekt, denn dieser Zeiger dreht sich tatsächlich im Ortsraum. Die Achsenbeschriftung der x-Achse fehlt dort. Da hast Du recht).
4. Du schreibst: Auf die Fülle dessen, was du ständig neu produziert, kann ich wirklich nicht komplett eingehen. (Bleib schön zurückhaltend: Du gehst ja auch auf meine Kritik nicht ein.) Ein bisschen Satzbauänderung ist sicher hinzubekommen, nur ist sie mit dem nichtsnutzigen Begriff Zeiger verbunden. Was habe ich Deiner Meinung nach übergangen? Wenn es Klärungsbedarf gibt, gehe ich gerne darauf ein. Die Änderung des Satzbaus war nicht mit dem Begriff Zeiger verbunden. Grammatikalisch würde der Satz auch mit "Strecke" statt Zeiger funktionieren. Allerdings ist der Begriff Zeiger der richtige und nicht nichtsnutzig.--Pyrrhocorax (Diskussion) 13:41, 15. Aug. 2013 (CEST)

1. „Warum in Dreiteufelsnamen weigerst Du Dich, für dieses Ding den vernünftigen Fachbegriff zu verwenden?“ Weil der an dieser Stelle kein vernünftiger Fachbegriff ist. Der Begriff Zeiger wird in seinem Bezugsartikel nicht erklärt, nur dass er rotiert und eine Länge hat; seine Natur bleibt offen: anfangs ist er wohl reell, später eine komplexe Zahl oder Größe. Auf diese Unbestimmtheit habe ich dich zweimal hingewiesen, aber das hast du übergangen.
2. In der Fachliteratur wird der Begriff Zeiger im Sinn von komplexe Größe verwendet. Dabei ist es gar nicht erforderlich, für eine harmonische Schwingung auf komplexe Größen zu gehen; sie sind an dieser Stelle nur ein überflüssiger mathematischer Überbau. Darauf habe ich dich zweimal hingewiesen, aber das hast du übergangen.
3. Du hast geschrieben: „Es ist keine "Strecke", die da rotiert. Strecken haben die Dimension von Längen.“ Ich habe erwidert: „Mach dich duch nicht lächerlich mit deiner Dimension Länge. Unter Zeigermodell steht doch für ${\hat {y}}$ auch nur „Länge des Zeigers“, die dann „Amplitude der Schwingung“ bedeutet, mit einer Einheit, die beliebig ist.“ Aber das hast du übergangen.
4. Du fragst nach dem in der Zeichnung auftauchenden Zeiger, der anscheinend die Dimension einer Spannung hat. Lies nach im „Wikipedia-Artikel, wo alles drinsteht, was man darüber wissen muss“: Amplitude der Schwingung … mit einer Einheit, die beliebig ist. Und wenn du dir eine elektrische Spannung vorstellst, hat das etwas mit der Erklärung des Phasenwinkels zu tun?
5. Jetzt kommt es noch dicker. Mit einmal schreibst du etwas von Vektor und „Vektorcharakter des Zeigers“. Vektoren in der klassischen Physik sind ja nun etwas ganz Anderes als Zeiger, z. B. in aller Regel nicht komplex. Ausnahmsweise bin ich dir dankbar für deinen Beitrag, denn er liefert mir das Beispiel zu meiner Aussage: „Der Begriff Zeiger ist ein mißverständlicher (bzw. vielfach mißbrauchter) Begriff“. Genau diese Vermischung der Begriffe ist es, die dem Begriff Zeiger in früheren Jahren vermehrt angehaftet hat; diese ist der Grund für meine Aussage. Inzwischen haben die Meisten den Unterschied begriffen, und der Mißbrauch ist seltener geworden, aber du bist offenbar einer der wenigen mit der Unterscheidung Zurückgebliebenen.
6. Die Rotation, die „das rotierende Ding“ zur Veranschaulichung der harmonischen Schwingung ausführt, ist im wissenschaftlichen Sprachgebrauch weder mit dem Begriff Zeiger (zur Darstellung einer komplexen Größe) noch an den Begriff Vektor (zur Darstellung einer gerichteten Größe des euklidischen Raums) gekoppelt. Von daher sind beide Begriffe in Blick auf die Rotation nicht erforderlich.
7. Darüber hinaus hast du dich mit deinem Satz „Für die Einführung des Phasenwinkels ist aber der Vektorcharakter des Zeigers unerlässlich“ hoffnungslos verstiegen, denn dafür braucht man nur einen geraden Strich auf einer Zeichenebene, dem man die Fähigkeit zur Rotation um einen Endpunkt zuerkennt (und eine Bezugsachse durch den Drehpunkt für den Nullphasenwinkel).
8. Für „das rotierende Ding“ sollte zur möglichst verständlichen Darstellung das mathematisch Einfachste genommen werden (denk an die „omA-taugliche Motivation“, die du zuletzt noch herangezogen hast). Das Einfachste ist eine skalare und eben keine komplexe oder vektorielle Größe. Anschaulich jedem, der eine Winkelfunktion kennt, (außer einem) sofort naheliegend sind dazu die Strecke und der Radius. Es ist nicht nötig, einen Begriff einzuführen, über den man erst nachlesen muss in einem „Wikipedia-Artikel, wo alles drinsteht, was man darüber wissen muss“. Das hatte ich dir auch schon geschrieben, aber das hast du übergangen.
9. Wesentlich weiter oben habe ich dir geschrieben: Schade, dass es dir so schwer fällt, genau zu lesen. Ich habe immer stärker den Eindruck, es liegt nicht an einem unsauberen Lesen und Schreiben. Zu deinem Satz „Bitte geh einfach mal davon aus, dass alle, die sich an der Wikipedia aktiv beteiligen, auch eine Verbesserung anstreben“ hatte ich erwidert: Guter Wille alleine reicht nicht aus. Bei Weitem nicht!! Aber das übergehst du genauso wie meine Argumente gegen einen dir zwar lieben, aber undefinierten, darüberhinaus mißverständlichen bzw. mißbrauchten und hier vom mathematischen Aufwand überflüssigen Begriff.

Das Weitere, was du oben schreibst, ist von minderer Bedeutung und kann zurückgestellt werden. --der Saure 09:50, 17. Aug. 2013 (CEST)

Zu Deinen Punkten:

1. Wie Du selbst einräumst, ist es egal, ob man für die Darstellung des Zeigers rein geometrisch im Reellen oder eben in der komplexen Ebene arbeitet. Der Zeiger kann somit reell oder komplex sein. Dies wird im Artikel Zeigermodell so dargestellt. Was Du als Schwäche jenes Artikels ansiehst, ist in Wirklichkeit die Wiedergabe dessen, was Du selbst sagst. Übrigens: Wenn Du an dem Artikel Zeigermodell was auszusetzen hast, darfst Du das gerne dort ändern bzw. diskutieren. Hier geht es um den Begriff des Phasenwinkels.
2. dito.
3. Eben. Die Einheit und Dimension des Zeigers ist frei wählbar, je nachdem ob man eine Spannung, eine Stromstärke, eine mechanische Schwingung oder eine Schallwelle beschreiben will. Deswegen ist die Einheit beliebig. Den Zeiger als Strecke zu bezeichnen hieße, ihm die Dimension eines Weges zu geben. Im Artikel Zeigermodell ist mit Länge nicht Länge (Physik) sondern Vektor#Länge/Betrag eines Vektors gemeint.
4. Ich sagte nur, dass der Bezug auf die x-Achse, der da im Artikel stand, nicht korrekt ist, weil es in einem Zeigerdiagramm, in dem ein Spannungszeiger rotiert, keine x-Achse gebe. Die Beschriftung der horizontalen Achse mit x ist falsch. (Du brauchst Dich an diesem Punkt aber nicht aufzuhängen. Das ist eine Kleinigkeit. Wenn es die einzige Schwäche des Satzes gewesen wäre, hätte man das schnell korrigieren können. Diese Diskussion hat sich daran entzündet, dass ich den betreffenden Satz aus mehreren Gründen editiert habe. Du hast meinen Edit revertiert. Daher muss ich davon ausgehen, dass Du die ursprüngliche Version besser findest. Dann habe ich meine Version wieder hergestellt. Daraufhin hast Du den Satz komplett aus dem Artikel genommen.)
5. Natürlich ist der Vektorcharakter des Zeigers unerlässlich! Ein Vektor ist eine Größe, die einen Betrag und eine Richtung hat. Die Richtung wird hier durch den Phasenwinkel angegeben, der Betrag durch die Amplitude. Dies schrieb ich, weil Du den Begriff "Zeiger" durch Radius ersetzt hast. Der Radius ist aber keine Größe, die eine Richtung hat. Warum das Wort Radius besser sein soll als Zeiger, bleibt Dein Geheimnis.
6. dito.
7. Ein gerader Strich hat einen Vektorcharakter, denn er hat einen Anfang und ein Ende, einen Länge und eine Richtung.
8. Es kann ausdrücklich keine skalare Größe verwendet werden, um den Zeiger zu beschreiben. Skalare Größen können nämlich nicht rotieren. Außerdem schreibst Du, es sei nicht notwendig, einen Begriff an dieser Stelle einzuführen [...]. Warum ich ihn für notwendig halte, sollte mittlerweile klar sein. Ich halte ihn aber zudem für sinnvoll. Der Leser kann - wenn er auf den Link zum Zeigermodell findet - den Begriff der Phase mit dem Zeigerdiagramm vernetzen. Wenn man den Zeiger mit keiner Silbe im Artikel erwähnt, nimmt man ihm diese Chance.
9. Deine Gedanken über meine Lese- und Fachkompetenz habe ich ganz bewusst übergangen, weil das hier nicht ins Persönliche abdriften soll.

Sehr freundlich von Dir, dass Du dem, was ich weiter oben geschrieben habe, mindere Bedeutung zuschreibst.

So, ich mach jetzt mal Urlaub. --Pyrrhocorax (Diskussion) 11:07, 17. Aug. 2013 (CEST)

Schwingungen, Zeiger, Phasenwinkel

• Schwingungen sind ein abstraktes Konzept, das nichts mit einem "rotierenden Ding" zu tun hat. Die Schwingung einer elektrischen Spannung oder einer Temperatur hat nicht das Geringste mit rotierenden Dingen oder irgendwelchen anderen mechanischen Bewegungen irgendwelcher Körper zu tun.
• Komplexe Zeiger sind ein abstraktes mathematisches Konzept für die einfache Beschreibung und Berechnung von Schwingungen. Komplexe Zeiger zur Behandlung von Schwingungen haben nicht das Geringste mit "rotierenden Dingen" zu tun. Dass Schüler noch nicht mit komplexen Zeigern rechnen können ist bedauerlich, ändert aber nichts an der Tatsache, dass in der Schwingungslehre mit komplexen Zeigern gerechnet wird.
• Phasenwinkel sind ein abstraktes Konzept bei komplexen Zeigern zur Beschreibung und Berechnung von Schwingungen. Auch Phasenwinkel haben nicht das Geringste mit einem "rotierenden Ding" zu tun.

Offenbar führt es zu sehr vielen Verständnisproblemen bei der abstrakten Beschreibung von Schwingungen, dass dieser notwendige Abstraktionsschritt von "rotierenden Dingen" zur abstrakten Behandlung von Schwingungen, wegen fehlender mathematischer Voraussetzungen, in der Schule nicht durchgeführt und nicht einmal erklärt wird. -- Pewa (Diskussion) 09:25, 23. Aug. 2013 (CEST)

Phasenwinkel sind ein abstraktes Konzept bei komplexen Zeigern zur Beschreibung und Berechnung von Schwingungen. Und warum steht das so nicht gleich als erster Satz im Artikel? Das IST allgemeinverständlich, und erklärt dem Leser, worum es in diesem Lemma geht. --92.202.115.112 08:10, 24. Aug. 2013 (CEST)