Fenchel-Nielsen-Koordinaten

In der Mathematik dienen Fenchel-Nielsen-Koordinaten zur Parametrisierung des Raums hyperbolischer Metriken auf einer Fläche.

Markierte hyperbolische Flächen

Eine Fläche heißt hyperbolisch, wenn sie eine Riemannsche Metrik von konstanter Schnittkrümmung $-1$ mit totalgeodätischem Rand hat. Eine Fläche vom Geschlecht $g$ mit $n$ Randkomponenten ist genau dann hyperbolisch, wenn die Euler-Charakteristik $2-2g-n$ negativ ist.

Wir fixieren jetzt eine hyperbolische Fläche $\Sigma$. Eine Markierung einer hyperbolischen Fläche $S$ (vom selben Geschlecht mit derselben Anzahl von Randkomponenten) ist ein Homöomorphismus $\phi \colon \Sigma \to S$. Zwei Markierungen heißen äquivalent, wenn die Homöomorphismen homotop sind. Eine markierte hyperbolische Fläche (von gegebenem $g$ und $n$) ist dann ein Paar aus einer hyperbolischen Metrik und einer Äquivalenzklasse von Markierungen. Zwei isometrische hyperbolische Metriken entsprechen also unterschiedlichen markierten hyperbolischen Flächen, wenn die Isometrie nicht homotop zur Identität ist.

Der Fricke-Raum, häufig auch als Teichmüller-Raum ${\mathcal {T}}(S_{g,n})$ bezeichnet (womit eigentlich der Modulraum Riemannscher Flächen gemeint ist), ist der Modulraum markierter hyperbolischer Flächen zu gegebenem $g$ und $n$. Die Fenchel-Nielsen-Koordinaten sollen eine Parametrisierung dieses Raumes geben.

Fenchel-Nielsen-Koordinaten für Hosen

Eine Hose wird von 3 geschlossenen Kurven berandet.

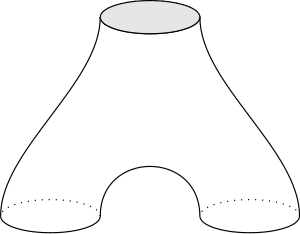
Sei $H$ eine Hose, also eine Fläche vom Geschlecht 0 mit drei Randkomponenten $\gamma _{1},\gamma _{2},\gamma _{3}$. Man erhält eine Hose aus zwei Sechsecken durch Identifizieren von drei (paarweise nicht-benachbarten) Kantenpaaren.

Aus zwei solchen Sechsecken setzt sich eine Hose zusammen.

Sei $(l_{1},l_{2},l_{3})$ ein Tripel positiver reeller Zahlen. Da es ein bis auf Kongruenz eindeutiges rechtwinkliges hyperbolisches Sechseck mit $l_{1}/2,l_{2}/2,l_{3}/2$ als Längen der rechts blau eingezeichneten Kanten gibt, erhält man eine eindeutige hyperbolische Metrik auf der Hose, so dass die drei Randkomponenten geschlossene Geodäten der Längen $l_{1},l_{2},l_{3}$ sind.

Man kann also den Raum der hyperbolischen Metriken auf der Hose parametrisieren durch

${\mathcal {T}}(H)\to \mathbb {R} _{+}^{3}$

$g\to (l_{g}(\gamma _{1}),l_{g}(\gamma _{2}),l_{g}(\gamma _{3}))$,

wobei $g$ die hyperbolische Metrik und $l_{g}(\gamma )$ die Länge der Kurve $\gamma$ in der Metrik $g$ bezeichnet.

Hosenzerlegung

Die Fläche vom Geschlecht 2 mit 4 Randkomponenten kann in 6 Hosen zerlegt werden.

Man kann mehrere Hosen entlang einiger ihrer Randkomponenten verkleben, wodurch man kompliziertere Flächen erhält. Die entsprechende Zerlegung der resultierenden Fläche wird als Hosenzerlegung bezeichnet.

Eine Fläche vom Geschlecht $g$ mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n} Randkomponenten besitzt genau dann eine Hosenzerlegung, wenn

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2(g-1)+n>0} ,

also wenn entweder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g\ge 2} oder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g=1,n\ge 1} oder Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle g=0,n\ge 3} ist. Eine Fläche kann im Allgemeinen mehrere unterschiedliche Hosenzerlegungen haben. Die Anzahl der Hosen in jeder Hosenzerlegung ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2(g-1)+n} . Die Anzahl der zerlegenden Kurven ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 3(g-1)+n} .

Twist-Parameter

Für zwei Randkomponenten einer hyperbolischen Hose gibt es eine eindeutige, sie verbindende kürzeste Geodäte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta} . Sei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta} eine andere die beiden Randkomponenten verbindende Kurve, und seien Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_1,N_2} Umgebungen der Randkomponenten. Man kann Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta} durch eine Isotopie außerhalb Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_1\cup N_2} mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta} übereinstimmen lassen. Die Twistzahlen von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \delta} bezüglich der beiden Randkomponenten sind dann definiert als die horizontale Verschiebung des Endpunkts innerhalb der Umgebungen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_1} bzw. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle N_2} .

Für eine markierte hyperbolische Fläche definiert man dann den Twist-Parameter Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \theta_i} bzgl. der geschlossenen Kurve Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \gamma_i} unter Zuhilfenahme einer Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \gamma_i} schneidenden geschlossenen Geodäte Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta_i\subset\Sigma} als Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \theta_g(\gamma_i)=2\pi\frac{t-t^\prime}{l_g(\gamma_i)}} , wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle t^\prime} die Twistzahlen bzgl. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \gamma_i} der als Durchschnitt von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \beta_i} mit den beiden von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \gamma_i} berandeten Hosen entstehenden Bögen sind.

Man beachte, dass die Twist-Parameter Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \alpha+2\pi} zwar isometrischen Flächen, aber unterschiedlichen markierten hyperbolischen Flächen entsprechen: der Dehn-Twist an Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \gamma_i} ist nicht homotop zur Identität.

Fenchel-Nielsen-Koordinaten

Als Fenchel-Nielsen-Koordinaten einer markierten hyperbolischen Fläche Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle X} (zu einer gewählten Hosenzerlegung aus geschlossenen Kurven Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \gamma_1,\ldots,\gamma_{3g-3+n}} ) bezeichnet man das Tupel

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (l_X(\gamma_1),\ldots,l_X(\gamma_{3g-3+n},\theta_X(\gamma_1),\ldots,\theta_X(\gamma_{3g-3+n}))\in\R_+^{3g-3+n}\times\R^{3g-3+n},}

wobei Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l_X(\gamma_i)} die Länge der geschlossenen Geodäte und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \theta_X(\gamma_i)} ihren Twist-Parameter bezeichnet.

Die Fenchel-Nielsen-Koordinaten geben einen Homöomorphismus Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle {\mathcal T}(S_{g,n})\simeq \R_+^{3g-3+n}\times\R^{3g-3+n}.}

Literatur

• W. Fenchel, J. Nielsen: Discontinuous groups of isometries in the hyperbolic plane. Edited by Asmus L. Schmidt. de Gruyter Studies in Mathematics 29, Berlin: Walter de Gruyter, 2003
• R. Benedetti, C. Petronio: Lectures on hyperbolic geometry. Universitext. Springer-Verlag, Berlin 1992, ISBN 3-540-55534-X.
• B. Farb, D. Margalit: A primer on mapping class groups. (= Princeton Mathematical Series. 49). Princeton University Press, Princeton, NJ 2012, ISBN 978-0-691-14794-9. (online archiviert via archive.org; pdf)

Weblinks

• U. Hamenstädt: Teichmüller theory