Hertzscher Dipol

Entdeckung der elektromagnetischen Wellen durch Heinrich Hertz: Briefmarke von 1983

Der Hertz'sche Dipol (nach Heinrich Hertz), auch Elementardipol genannt, ist die Idealisierung eines Senders elektromagnetischer Strahlung (die auch Dipolstrahlung oder Dipolwelle genannt wird) und dient der Berechnung der Abstrahlung realer Antennen sowie als Bezugsantenne, um die Richtwirkung einer Antenne als Gewinn zahlenmäßig zu erfassen. Eine Verallgemeinerung ergibt die (hier mitbehandelte) Multipolstrahlung.

Der Hertz'sche Dipol als Modell

Betrag der elektrischen Feldstärke $E=|{\vec {E}}|$ (farbig) und der Poynting-Vektor (schwarze Pfeile) im Nahfeld des vertikal in der Bildebene liegenden Dipols. Blaue/rote Farben bedeuten ein nach unten/oben orientiertes elektrisches Feld.

Datei:Animation Hertzscher Dipol.ogv

Dem Hertz'schen Dipol als Modell liegt ein elektrisches Dipolmoment ${\vec {p}}$, das sinusförmig mit der Kreisfrequenz $\omega$ variiert, zugrunde, dargestellt in komplexer Schreibweise

${\vec {p}}(t)\ ={\vec {p}}_{0}\mathrm {e} ^{-\mathrm {i} \omega t}$.

Ein solches reines Dipolmoment ohne räumliche Ausdehnung (Punktdipol) entsteht im Grenzübergang oszillierender Ladungsträger mit verschwindender Schwingungsamplitude (${\vec {l}}\to 0$) und divergierender Ladungsmenge ($q\to \infty$).

Exakte Gleichungen

Für das magnetische und elektrische Feld am durch Abstand $r$ und Richtung ${\vec {n}}$ gegebenen Ort gilt:

${\vec {H}}={\frac {\omega ^{3}}{4\pi c^{2}}}({\vec {n}}\times {\vec {p}})\left({\frac {1}{\rho }}+{\frac {\mathrm {i} }{\rho ^{2}}}\right)\mathrm {e} ^{\mathrm {i} (\rho -\omega t)}\quad$ (azimutal, verläuft in Breitenkreisen um die Dipolachse)

${\vec {E}}={\frac {\omega ^{3}}{4\pi \varepsilon c^{3}}}\left[({\vec {n}}\times {\vec {p}})\times {\vec {n}}\,{\frac {1}{\rho }}+\left(3{\vec {n}}({\vec {n}}\cdot {\vec {p}})-{\vec {p}}\right)\left({\frac {1}{\rho ^{3}}}-{\frac {\mathrm {i} }{\rho ^{2}}}\right)\right]\mathrm {e} ^{\mathrm {i} (\rho -\omega t)}\quad$ (Meridionalebene bzw. meridional „Richtung Süden“ und radial)

Darin ist

• $c$ die Lichtgeschwindigkeit
• $\rho ={\tfrac {\omega r}{c}}={\tfrac {2\pi r}{\lambda }},$ mit der Wellenlänge $\lambda$ der Strahlung.
• $\varepsilon$ die absolute Permittivität, im Vakuum also $\varepsilon _{0}$. Es wird an dieser Stelle also das Internationale Einheitensystem (SI) benutzt, obwohl das äquivalente cgs-System manche Formeln vereinfacht

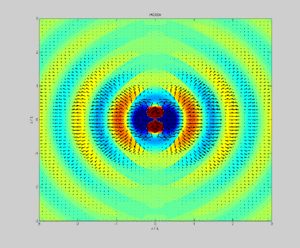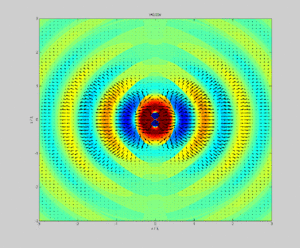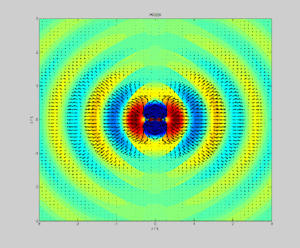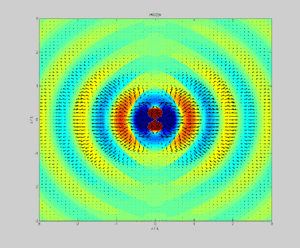
Aus diesen Gleichungen für den Hertz'schen Dipol lassen sich, im Gegensatz zu allen anderen Antennentypen, die Ausbreitungsgeschwindigkeiten der Wellenfronten analytisch berechnen. Insgesamt ergibt sich ein Strahlungsfeld, das zu jedem Zeitpunkt geschlossene Feldlinien hat, mit einer in allen Lehrbüchern wiedergegebenen charakteristischen Nierenform (siehe z. B. das Außenfeld in Bild 1). Betont man zusätzlich die Zeitabhängigkeit, so erhält man obige Animation, welche in realistischer Weise u. a. die Phasengeschwindigkeit $v_{p}$, die Gruppengeschwindigkeit $v_{g}$ und die Ausbreitungsgeschwindigkeit der Energie $v_{e}$ in Einheiten der Lichtgeschwindigkeit $c$ als Funktion der Entfernung zur Quelle in Einheiten der Kreis-Wellenzahl $k={\tfrac {\omega }{c}}={\tfrac {2\pi }{\lambda }}$ ergibt. Für große Abstände nähern sich alle diese Geschwindigkeiten der Lichtgeschwindigkeit. Im Nahfeld gibt nur $v_{e}$ die Geschwindigkeit der Signalausbreitung richtig wieder.

Kugelkoordinaten mit zugehöriger vom Ort abhängigen Orthogonalbasis

Durch Zerlegen der Felder in die Komponenten der Kugelkoordinaten ergibt sich die zweite besonders in den Ingenieurswissenschaften gängige Darstellung. Hier wird auch die Ausrichtung des Feldes schnell deutlich.

Radial	$H_{\text{r}}=0$	$E_{\text{r}}={\vec {e}}_{\text{r}}\cdot {\vec {E}}=2|{\vec {p}}|\cos \theta \,{\frac {\omega ^{3}}{4\pi \varepsilon c^{3}}}\left({\frac {1}{\rho ^{3}}}-{\frac {\mathrm {i} }{\rho ^{2}}}\right)\mathrm {e} ^{\mathrm {i} (\rho -\omega t)}$
Meridional	$H_{\theta }=0$	$E_{\theta }={\vec {e}}_{\theta }\cdot {\vec {E}}=|{\vec {E}}-{\vec {E}}_{\text{r}}|=-\sin \theta \,|{\vec {p}}|{\frac {\omega ^{3}}{4\pi \varepsilon c^{3}}}\left({\frac {1}{\rho }}-{\frac {1}{\rho ^{3}}}+{\frac {\mathrm {i} }{\rho ^{2}}}\right)\mathrm {e} ^{\mathrm {i} (\rho -\omega t)}$
Azimutal	$H_{\varphi }={\vec {e}}_{\varphi }\cdot {\vec {H}}=-|{\vec {p}}|\,\sin \theta \,{\frac {\omega ^{3}}{4\pi c^{2}}}\left({\frac {1}{\rho }}+{\frac {\mathrm {i} }{\rho ^{2}}}\right)\mathrm {e} ^{\mathrm {i} (\rho -\omega t)}$	$E_{\varphi }=0$

Nah- und Fernbereich

Im Nahbereich, $r\ll \lambda$, dominiert wegen des Terms $\propto \rho ^{-3}$ das elektrische Feld, während das Magnetfeld vernachlässigt werden kann: Es ist etwa im Verhältnis (r/λ) schwächer und in Gegenphase zum elektrischen Feld (d. h. wenn das eine Feld maximal ist, hat das andere ein Minimum).  ${\vec {E}}$ verhält sich hier wie ein quasistatisches (d. h. langsam oszillierendes) Dipolfeld, und das Magnetfeld ist, analog zu einer schwachen induktiven Impedanz im Verhältnis zum starken Ohmschen Widerstand, vernachlässigbar. Das Magnetfeld steht senkrecht auf dem Radiusvektor und dem elektrischen Feld.

Die elektrische Feldstärke ist hier $\propto \rho ^{-3}$, Winkel- und Frequenzabhängigkeit entsprechen dem langsam oszillierenden Dipolmoment.

Im Fernbereich, $r\gg \lambda$, stehen zusätzlich Radiusvektor und elektrisches Feld nahezu orthogonal zueinander. Magnetfeld und elektrisches Feld schwingen in Gleichphase. Bis auf im SI-System willkürlich gewählte Konstanten haben sie dieselbe funktionale Abhängigkeit von den Variablen. Im cgs-System, wo diese Konstanten gleich Eins gesetzt werden, gilt $|{\vec {E}}|=|{\vec {H}}|\ \propto |{\vec {p}}|\ \omega ^{2}/r$ (bzw. Strahlungsintensität  $\propto |{\vec {p}}|^{2}\omega ^{4}$).

Damit sich die Feldlinien des elektrischen Feldes schließen, gibt es noch eine radiale Komponente. Im Nahbereich gilt dafür ein Term $\propto \rho ^{-3}$ und im Fernbereich dominiert der Term $\propto \rho ^{-2}$.

Konsequenzen

Die letzte Formel hat viele Konsequenzen, u. a. für die gesamte Radio- und Fernsehtechnik. Die blaue Färbung des Himmels entsteht dadurch, dass die Strahlung der Sonne die Luftmoleküle zu Dipolstrahlung anregt (ein Beispiel für Rayleigh-Streuung). Obwohl das Sonnenspektrum sein Maximum bei $f=(\omega /2\pi )\sim 550\cdot 10^{12}~\mathrm {Hz}$ im grünen Spektralbereich hat, dominiert in der Abstrahlung blaues Licht (Frequenzen um den höheren Wert $f^{\prime }:=(\omega ^{\prime }/2\pi )\sim 650\cdot 10^{12}~\mathrm {Hz}$). Das ungefähre Verhältnis $(\omega ^{\prime }/\omega )^{4}\cong (6{,}5/5{,}5)^{4}$ entspricht nahezu einer Verdoppelung der Strahlungsintensität beim Übergang von einer grünen zu einer blauen Frequenz bei festem Dipolmoment. Ferner ist die angegebene Formel auch für die heute alltäglich gewordene Mobiltelefonie relevant. Dabei erfolgt die Kommunikation über die vom Mobiltelefon zu den nächstgelegenen Vermittlungsknoten ausgehende Dipolstrahlung, deren Frequenzbereich (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \sim 10^9~\mathrm{Hz}}  ) genügend hoch ist, dass trotz minimalen Energieverbrauchs der Mobiltelefone die Signalintensität für die Informationsübertragung ausreicht. Zugleich liegen die Frequenzen der Mobiltelefonie noch im biologisch unschädlichen Bereich, im Gegensatz etwa zur Röntgenstrahlung.

Von der Fernfeldnäherung zum Antennendiagramm

Im Fernfeld sind die Terme mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \rho^{-2}} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \rho^{-3}} vernachlässigbar. Schreibt man nur die dominierenden Terme auf, so folgt:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \vec H &\cong \frac{\omega^2}{4\pi c r}(\vec n \times \vec p)\,\mathrm{e}^{\mathrm{i} (\rho-\omega t)}\\ \vec E &\cong \frac{\omega^2}{4\pi \varepsilon c^2 r} (\vec n\times\vec p)\times\vec n\,\mathrm{e}^{\mathrm{i} (\rho-\omega t)} \end{align}}

Betrag der Feldstärke im Fernfeld eines vertikalen Hertz'schen Dipols in Kugelkoordinaten

Der Betrag des gemeinsamen Faktors Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec n \times \vec p} enthält die Richtungsabhängigkeit der Feldstärke. Sie variiert wie Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \cos\varphi} mit dem Winkel Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varphi} zur Äquatorebene und ist unabhängig vom Azimut (siehe nebenstehendes Antennendiagramm).

Der Poynting-Vektor Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{S}=\vec{E}\times\vec{H}} gibt die Energieflussdichte an. Sein Betrag, zeitlich gemittelt, ist im Fernfeld

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \langle|\vec{S}(\theta ,r)|\rangle =\frac{1}{2}\,\frac{\omega^2|\vec p|}{4\pi \varepsilon c^2 r}\,\frac{\omega^2|\vec p|}{4\pi c r}\,(1-\cos^2\theta )}

und bis auf einen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 1/r^2} -Faktor gleich der Strahlungsintensität

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle I(\theta )=\frac{\omega^4|\vec p|^2}{32\pi^2\varepsilon c^3}\,(1-\cos^2\theta ).}

Dabei ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \theta} der von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec p} aus gemessene Polarwinkel des Vektors Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec r.} Vom Azimutalwinkel Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varphi} hängt das Ergebnis dagegen nicht ab. Die Ausstrahlung erreicht also ihr Maximum in den Richtungen senkrecht zu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec p,} also senkrecht zur Antenne. In Antennenrichtung selbst verschwindet sie.

Integriert man über alle Richtungen, so ergibt sich die insgesamt ins Fernfeld abgestrahlte Leistung zu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle P = \tfrac{\omega^4|\vec p|^2}{12 \pi \varepsilon c^3} } . Dieses Ergebnis stammt von der Integration über den Raumwinkel. Bei isotroper Verteilung ergäbe sich stattdessen eine Strahlungsintensität von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \bar{I} = \tfrac{\omega^4|\vec p|^2}{48 \pi^2 \varepsilon c^3}. } Das als Antennengewinn bezeichnete Verhältnis Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \tfrac{I(0)}{\bar{I}}} beträgt im Vakuum also 1,5 (etwa 1,76 dBi).

Verallgemeinerung: Multipolstrahlung

Definitionen

Die Zuführung eines Wechselstroms der Kreisfrequenz Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \omega} zu einer Antenne der Länge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle l} erzeugt also einen periodisch oszillierenden elektrischen Dipolvektor mit der Antennenrichtung (z-Richtung) als Dipolrichtung. (Das elektrische Dipolmoment ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \propto Q(t)\cdot l,} wobei Q(t) die periodisch oszillierende elektrische Ladung ist.)

Ebenso wird durch ein in der (x,y)-Ebene auf einem Kreis mit Radius Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta R} umlaufendes Teilchen mit der konstanten Ladung Q₀ ein magnetischer Dipolvektor erzeugt, der per Konvention ebenfalls die z-Richtung hat und entsprechend dem Umlaufsinn zirkular polarisiert ist. (Das magnetische Dipolmoment ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \propto\pi (\Delta R)^2\cdot Q_0 \ ;} die Kreisfrequenz des Umlaufs ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \omega} .)

Magnetische Dipolstrahlung ist also wegen der quadratischen Abhängigkeit des Momentes von der (im Vergleich zu λ) kleinen Länge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \Delta R} von vornherein eine Größenordnung schwächer als elektrische Dipolstrahlung. Für diese gilt dagegen die schon bekannte lineare Beziehung.

Zwei geringfügig gegeneinander verschobene entgegensetzt-gleiche Dipolvektoren ergeben einen sog. „Quadrupoltensor“, zwei geringfügig gegeneinander verschobene entgegengesetzt-gleiche Quadrupole einen „Oktupol“ usw. Die Zahl der Freiheitsgrade erhöht sich dabei jedes Mal um zwei, nicht um drei, weil bei der Richtung der Verschiebung nur die beiden Winkelkoordinaten senkrecht zur z-Achse involviert sind.

Anstelle der kartesischen Koordinaten (x, y, z) werden im Folgenden Kugelkoordinaten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (r,\theta ,\varphi )} benutzt, die in der üblichen Weise miteinander zusammenhängen.

Formel

Die zugehörige Verallgemeinerung der Hertzschen Dipolstrahlung ist die sogenannte Multipolstrahlung. Anstelle des Dipolvektors treten elektrische plus magnetische Multipolmomente Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_{\ell m}^{(E)}} bzw. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_{\ell m}^{(M)}} auf, wobei die Indizes Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ell} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m} sich auf die polaren bzw. azimutalen Winkelvariablen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \theta} bzw. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \varphi} der Kugelkoordinaten beziehen. Die allgemeine Formel ist nach John David Jackson

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} \vec{E}(\vec{x},t) &= \sum_{\ell=1}^\infty \sum_{m=-\ell}^\ell \left[a_{\ell m}^{(M)} h_\ell^{(1)}(kr) \vec{X}_{\ell m}(\theta, \varphi)+\frac{\mathrm iZ_0}{k}a_{\ell m}^{(E)}\vec{\nabla}\times(h_\ell^{(1)}(kr)\vec{X}_{\ell m}(\theta, \varphi))\right]\mathrm{e}^{-\mathrm i\omega t}\\ \vec{H}(\vec{x},t) &= \sum_{\ell=1}^\infty \sum_{m=-\ell}^\ell \left[a_{\ell m}^{(E)} h_\ell^{(1)}(kr) \vec{X}_{\ell m}(\theta, \varphi)-\frac{\mathrm i}{kZ_0}a_{\ell m}^{(M)}\vec{\nabla}\times(h_\ell^{(1)}(kr)\vec{X}_{\ell m}(\theta, \varphi))\right]\mathrm{e}^{-\mathrm i\omega t} \end{align}}

Dies entspricht ungefähr der Vertauschung von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec E} und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec H} unter Berücksichtigung des Vorzeichens ( +iZ₀ → -i/Z₀), analog zur formalen Vertauschungssymmetrie der freien Maxwellschen Gleichungen im cgs-System (Vakuum, Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{B}=\vec{H}} , Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec{D}=\vec{E}} ):

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \operatorname{rot}\vec E + \frac{1}{c}\frac{\partial \vec H}{\partial t} =0, \quad \operatorname{rot}\vec H -\frac{1}{c}\frac{\partial \vec E}{\partial t} =0. }

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Z_0} ist die Vakuumimpedanz Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \textstyle\sqrt{\mu_0/\varepsilon_0}.} Die Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec X_{\ell m}} sind wie folgt definiert:

Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec X_{\ell m} = \frac{1}{\sqrt{\ell(\ell+1)}} \vec L Y_{\ell m}}

mit den Kugelflächenfunktionen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y_{\ell m}} und dem Drehimpulsoperator Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec L = - \mathrm i \vec r \times \vec \nabla} .

Die Gewichtsfaktoren Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_{\ell m}^{(E)}} bzw. Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle a_{\ell m}^{(M)}} beschreiben für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ell=1} elektrische bzw. magnetische Dipolstrahlung bzw. für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ell=2} Quadrupolstrahlung, jeweils mit Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 2\ell+1} verschiedenen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m} -Werten. Man hat also für die aufeinander folgenden Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ell} -Werte drei bzw. fünf Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle m} -Werte. Im Fernbereich kann die Radialfunktion Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle h_\ell^{(1)}(kr),} eine sphärische Besselfunktion, vereinfacht werden zu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \textstyle h_\ell^{(1)}(kr)\cong (-\mathrm i)^{\ell+1}\frac{\exp(\mathrm i k r)}{k r},} in Übereinstimmung mit den obigen Formeln. Die Größe k schließlich ist gleich ω/c.

Nah- und Fernfeld

Im Nahbereich sind die Feldkomponenten jetzt – bei komplizierter Richtungsabhängigkeit, gegeben durch die Kugelflächenfunktionen Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle Y_{\ell m}(\theta ,\varphi )}  –  proportional zu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle r^{-(\ell+2)}.}  Im Fernbereich sind dagegen nach wie vor alle Komponenten Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \propto 1/r \ ,} und die elektrischen bzw. magnetischen Felder sowie der Radiusvektor sind wie bei ebenen elektromagnetischen Wellen paarweise orthogonal zueinander.

Monopolstrahlung würde Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \ell=0} entsprechen. Diese kann nicht auftreten, da das Außenfeld einer kleinen geladenen Kugel unabhängig vom oszillierenden Kugelradius nach dem Satz von Gauß nur durch die konstante Gesamtladung gegeben ist. Dies muss nicht als zusätzliche Annahme gefordert werden, denn insbesondere ist Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \vec X_{00} = 0} .

Siehe auch

• Hertzscher Oszillator

Literatur

• John D. Jackson: Klassische Elektrodynamik. 3. Auflage. de Gruyter, 2002, ISBN 3-11-016502-3.
• Klaus Kark: Antennen und Strahlungsfelder : elektromagnetische Wellen auf Leitungen, im Freiraum und ihre Abstrahlung. Vieweg, Wiesbaden 2006, ISBN 3-8348-0216-6.

Weblinks

• Berechnungen und Animationen zum Hertz'schen Dipol
• Animationen zur Abstrahlung vom Hertz'schen Dipol (LMU München, Physikdidaktik)