Starke Wechselwirkung

Die starke Wechselwirkung (auch starke Kraft, Gluonenkraft, Farbkraft) ist eine der vier Grundkräfte der Physik. Mit ihr wird die Bindung zwischen den Quarks in den Hadronen erklärt. Ihre Austauschteilchen sind die Gluonen.

Vor der Einführung des Quark-Modells wurde als starke Wechselwirkung lediglich die Anziehungskraft zwischen den Nukleonen des Atomkerns bezeichnet, d. h. Protonen und Neutronen. Auch heute noch ist mit der starken Wechselwirkung oft nur diese Restwechselwirkung gemeint, aus historischen Gründen auch Kernkraft oder starke Kernkraft genannt.

Feynman-Diagramme zu den fundamentalen Kopplungsmöglichkeiten der starken Wechselwirkung, a) Abstrahlung eines Gluons, b) Aufspaltung eines Gluons c) ,d) „Selbstkopplung“ der Gluonen.

Bindung zwischen Quarks

Wechselwirkung innerhalb eines Neutrons (Beispiel). Die Gluonen sind dargestellt als Punkte mit der Farbladung im Zentrum und der Antifarbe am Rand.

Nach der Quantenchromodynamik (im Folgenden: QCD) wird die starke Wechselwirkung – wie die elektromagnetische und die schwache Wechselwirkung – durch den Austausch von Eichbosonen beschrieben. Die Austauschteilchen der starken Wechselwirkung werden als Gluonen bezeichnet, von denen es acht Sorten (unterschiedliche Farbladungszustände) gibt. Die Gluonen übertragen eine Farbladung zwischen den Quarks. Ein Gluon kann dabei mit anderen Gluonen interagieren und Farbladungen austauschen.

Potential zwischen zwei Quarks in Abhängigkeit ihres Abstands. Zusätzlich sind die mittleren Radien verschiedener Quark-Antiquark-Zustände gekennzeichnet.

Die Anziehungskraft zwischen Quarks bleibt auch bei steigender Entfernung konstant, anders als z. B. bei der Coulombkraft, bei der es mit steigendem Abstand immer leichter wird, zwei sich anziehende Teilchen zu trennen. Sie ist damit grob vergleichbar mit einem Gummiseil oder einer Zugfeder. Wird der Abstand zu groß, „reißt“ das Seil in dieser Analogie und es wird ein Meson gebildet durch Erzeugung eines Quark-Antiquark-Paares aus dem Vakuum. Bei kleinem Abstand können die Quarks wie freie Teilchen betrachtet werden (asymptotische Freiheit). Mit größerem Abstand bewirkt die zunehmende Wechselwirkungsenergie, dass die Quarks den Charakter selbstständiger Teilchen verlieren, weswegen sie nicht als freie Teilchen beobachtet werden können (Confinement).

Bindung zwischen Nukleonen

Obwohl Nukleonen immer die Farbladung null haben, gibt es zwischen ihnen eine Restwechselwirkung oder Kernkraft (entfernt vergleichbar den Van-der-Waals-Kräften, die man als elektromagnetische Restwechselwirkungen zwischen elektrisch neutralen Atomen und/oder Molekülen ansehen kann).

Die Reichweite der Anziehung durch die Restwechselwirkung liegt bei etwa 2,5 Femtometern (fm). Bei diesem Wert des Abstands $r$ ist sie vergleichbar stark wie die elektrische Abstoßung (Coulombkraft) zwischen den Protonen und bei kürzeren Abständen ist sie stärker als die Coulombkraft. Oberhalb dieses Abstandes dagegen nimmt die Anziehung schneller ab als die Coulombkraft, die proportional zu $1/r^{2}$ sinkt. Dieses Zusammenspiel der beiden Grundkräfte erklärt den Zusammenhalt und die Größenordnung der Atomkerne, aber z. B. auch die Spaltung schwerer Kerne.

Auf sehr kurze Abstände wirkt die Kernkraft abstoßend, entsprechend einem harten Kern (Hard Core) von 0,4 bis 0,5 fm. Außerdem ist sie Spin-abhängig: sie ist stärker bei parallelen Spins als bei antiparallelen, so dass das Deuteron (bestehend aus einem Neutron und einem Proton) nur für parallele Spins (Gesamtspin 1) gebunden ist, und Diproton und Dineutron (mit antiparallelen Spins aufgrund des Pauli-Prinzips) nicht gebunden sind. Neben dem Zentralpotential-Anteil und dem Spin-Spin-Wechselwirkungsanteil hat sie auch einen Tensoranteil und einen Spin-Bahn-Anteil.

Vor der Einführung des Quark-Modells wurden die Restwechselwirkung und ihre geringe Reichweite mit einer effektiven Theorie erklärt: durch eine Yukawa-Wechselwirkung zwischen Nukleonen und Pionen (Pion-Austauschmodell). Die geringe Reichweite wird durch die von Null verschiedene Masse der Pionen erklärt, die im Yukawa-Potential zu einer exponentiellen Abschwächung auf größeren Abständen führt. Außerdem wurde in den Nukleon-Nukleon-Potential-Modellen der Austausch weiterer Mesonen berücksichtigt (wie dem Rho-Meson). Da Berechnungen der Kernkraft mit der QCD bisher nicht möglich sind, benutzt man zum Beispiel in der Beschreibung der Nukleon-Nukleon-Streuung verschiedene phänomenologisch angepasste Potentiale, die auf Mesonenaustauschmodellen basieren (wie das Bonn-Potential).

Erklärung der Restwechselwirkung

Feynman-Diagramm einer starken Proton-Neutron-Wechselwirkung vermittelt durch ein neutrales Pion. Die Zeit-Achse verläuft von links nach rechts.

Dasselbe Diagramm mit den einzelnen Konstituenten-Quarks gezeigt, um darzustellen, wie die fundamentale starke Wechselwirkung eine „Kernkraft“ erzeugt. Gerade Linien sind Quarks, vielfarbige Schleifen Gluonen (Träger der Grundkraft). Andere Gluonen, welche Proton, Neutron und Pion (im „Flug“) zusammenhalten, sind nicht dargestellt.

Eine Animation der Wechselwirkung, die zwei kleinen farbigen Punkte sind Gluonen. Anti-Farben können diesem Diagramm entnommen werden. (größere Version)

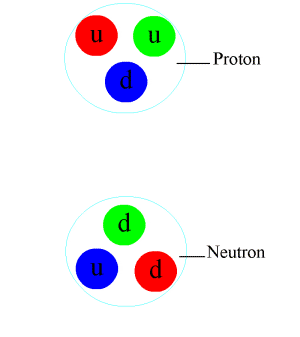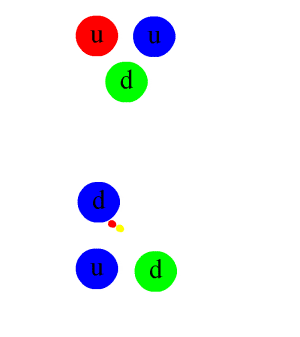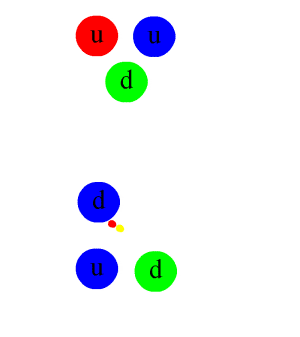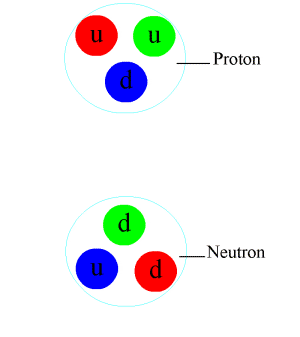
Zwischen Atomen ist das abstoßende Potential bei kleinen Abständen eine Folge des Pauli-Prinzips für die Elektronenzustände. Bei Annäherung zweier Nukleonen mit sechs Quarks hat jedes Quark aber erheblich mehr Freiheitsgrade im niedrigsten Zustand (Bahndrehimpuls l=0): neben Spin (2 Zustände) noch eine Farbladung (3 Zustände) und Isospin (2 Zustände), zusammen also 12, auf die sich die sechs Quarks nach dem Pauli-Prinzip verteilen können. Das Pauli-Prinzip ist hier nicht unmittelbar für die Abstoßung verantwortlich, die sich unterhalb etwa 0,8 fm bemerkbar macht. Der Grund liegt vielmehr in der starken Spin-Spin-Wechselwirkung der Quarks, die sich augenfällig darin ausdrückt, dass die Delta-Resonanz (mit parallelen Spins der drei Quarks) eine um etwa ein Drittel höhere Masse als das Proton hat. Stehen also die Spins der Quarks parallel zueinander, so nimmt die potentielle Energie des Systems zu. Dies gilt auch bei sich überlappenden Nukleonen, und zwar umso stärker, je geringer der Abstand der Nukleonen voneinander ist. Versuchen die Quarks durch Umkehrung des Spins ihre chromomagnetische Energie zu minimieren, gelingt dies nur durch Übergang in einen energetisch höheren Bahndrehimpulszustand (l=1).

Mit noch größerem Abstand voneinander gelangen die Nukleonen in den anziehenden Teil der starken Wechselwirkung. Hierbei spielt weniger der Quark-Quark-Austausch (zwei Quarks sind gleichzeitig beiden beteiligten Nukleonen zugeordnet), den man in Analogie zur kovalenten Bindung erwartet, eine Rolle, als vielmehr der von farbneutralen Quark-Antiquark-Paaren (Mesonen) aus dem Seequark-Anteil der Nukleonwellenfunktion in der QCD.

Eine vollständige Beschreibung der Kernkraft aus der Quantenchromodynamik ist jedoch bisher nicht möglich.

Einordnung der starken Wechselwirkung

Fundamentale Wechselwirkungen und ihre Beschreibungen (Theorien in frühem Stadium der Entwicklung sind grau hinterlegt.)
	Starke Wechselwirkung	Elektromagnetische Wechselwirkung		Schwache Wechselwirkung	Gravitation
klassisch		Elektrostatik	Magnetostatik		Newtonsches Gravitationsgesetz
		Elektrodynamik			Allgemeine Relativitätstheorie
quanten- theoretisch	Quanten­chromodynamik (Standardmodell)	Quanten­elektrodynamik		Fermi-Theorie	Quanten­gravitation (?)
		Elektroschwache Wechselwirkung (Standardmodell)
	Große vereinheitlichte Theorie (?)
	Weltformel („Theorie von Allem“) (?)

Literatur

• Manfred Böhm, Ansgar Denner, Hans Joos: Gauge theories of the strong and electroweak interaction, Teubner-Verlag, Stuttgart 2001, ISBN 978-3-519-23045-8 (deutsches Original: Becher-Böhm-Joos, Eichtheorien der starken und elektroschwachen Wechselwirkung) – ein Standardwerk für die Theorie
• Bogdan Povh, Klaus Rith, Christoph Scholz, Frank Zetsche Teilchen und Kerne, 8. Auflage, Springer Verlag 2009
• Wolfgang Wild Kernkräfte und Kernstruktur, Teil 1,2, Physikalische Blätter 1977, S. 298, 356, Teil 1, Teil 2

Weblinks

• Marc Gänsler: Die starke Wechselwirkung. In: Einführung: Die 4 Grundkräfte der Physik, abgerufen 30. Januar 2009.
• Gluonen und die starke Kraft. DESYs Kwork Quark, »Teilchenphysik für alle«

Einzelnachweise

Die vier Grundkräfte der Physik

Starke Wechselwirkung | Elektromagnetische Wechselwirkung | Schwache Wechselwirkung | Gravitation