Kryptographie

Kryptographie bzw. Kryptografie (altgriechisch κρυπτός kryptós, deutsch ‚verborgen‘, ‚geheim‘ und

γράφειν

) ist ursprünglich die Wissenschaft der Verschlüsselung von Informationen. Heute befasst sie sich auch allgemein mit dem Thema Informationssicherheit, also der Konzeption, Definition und Konstruktion von Informationssystemen, die widerstandsfähig gegen Manipulation und unbefugtes Lesen sind.

Terminologie

Der Begriff Kryptographie bedeutet Geheimschrift. Die Kryptographie befasste sich historisch mit der Erzeugung, Betrachtung und Beschreibung von Verfahren, um „geheim zu schreiben“, also mit Verschlüsselungsverfahren. Seit Ende des 20. Jahrhunderts werden sie zur sicheren Kommunikation und für sichere Berechnungen eingesetzt.

Kryptoanalyse (auch Kryptanalyse) bezeichnet hingegen die Erforschung und Anwendung von Methoden, mit denen kryptographische Verfahren gebrochen („geknackt“) werden können.

Ein Kryptosystem dient zur Geheimhaltung von übertragenen oder gespeicherten Informationen gegenüber Dritten.

Oft werden die Begriffe Kryptographie und Kryptologie gleichwertig benutzt, während sich z. B. beim US-Militär Kryptographie meist auf kryptographische Techniken bezieht und Kryptologie als Oberbegriff für Kryptographie und Kryptoanalyse verwendet wird. Die Kryptographie kann also auch als Teilgebiet der Kryptologie gesehen werden.

Das Untersuchen von Merkmalen einer Sprache, die Anwendung in der Kryptographie finden (z. B. Buchstabenkombinationen), wird Kryptolinguistik genannt.

Abgrenzung zur Steganographie

Sowohl Kryptographie als auch Steganographie haben zum Ziel, die Vertraulichkeit einer Nachricht zu schützen. Allerdings unterscheiden sie sich im Ansatzpunkt der Verfahren:

• Kryptographie verschlüsselt die Nachricht. Somit sorgt sie dafür, dass eine unbeteiligte dritte Person, die die (verschlüsselten) Daten zu Gesicht bekommt, die Bedeutung nicht erfassen kann.
• Steganographische Verfahren verbergen den Kanal, über den kommuniziert wird. Eine unbeteiligte dritte Person bleibt dadurch in Unkenntnis der Kommunikation.

Kryptographische und steganographische Verfahren können kombiniert werden. Beispielsweise führt eine Verschlüsselung (Kryptographie) einer Nachricht, die über einen verdeckten Kanal kommuniziert wird (Steganographie), dazu, dass selbst nach dem Entdecken und erfolgreichen Auslesen des Kanals der Inhalt der Nachricht geheim bleibt.

Ziele der Kryptographie

Die moderne Kryptographie hat vier Hauptziele zum Schutz von Datenbeständen, Nachrichten und/oder Übertragungskanälen:

1. Vertraulichkeit/Zugriffsschutz: Nur dazu berechtigte Personen sollen in der Lage sein, die Daten oder die Nachricht zu lesen oder Informationen über ihren Inhalt zu erlangen.
2. Integrität/Änderungsschutz: Die Daten müssen nachweislich vollständig und unverändert sein.
3. Authentizität/Fälschungsschutz: Der Urheber der Daten oder der Absender der Nachricht soll eindeutig identifizierbar sein, und seine Urheberschaft sollte nachprüfbar sein.
4. Verbindlichkeit/Nichtabstreitbarkeit: Der Urheber der Daten oder Absender einer Nachricht soll nicht in der Lage sein, seine Urheberschaft zu bestreiten, d. h., sie sollte sich gegenüber Dritten nachweisen lassen.

Kryptographische Verfahren und Systeme dienen nicht notwendigerweise gleichzeitig allen der hier aufgelisteten Ziele.

Methoden der Kryptographie

Kryptographische Verfahren werden unterteilt in die klassischen und modernen Verfahren.

• Methoden der klassischen Kryptographie: Solange für die Kryptographie noch keine elektronischen Rechner eingesetzt wurden, ersetzte man bei der Verschlüsselung (zu dieser Zeit die einzige Anwendung der Kryptographie) immer vollständige Buchstaben oder Buchstabengruppen. Solche Verfahren sind heute veraltet und unsicher.
  • Transposition: Die Buchstaben der Botschaft werden einfach anders angeordnet. Beispiel: Gartenzaunmethode oder Skytale.
  • Substitution: Die Buchstaben der Botschaft werden durch jeweils einen anderen Buchstaben oder ein Symbol ersetzt; siehe Monoalphabetische Substitution und Polyalphabetische Substitution. Beispiele dafür sind die Caesar-Verschlüsselung und die Vigenère-Verschlüsselung.
• Codebuch, ebenfalls ein klassisches Verfahren.
• Methoden der modernen Kryptographie: Entsprechend der Arbeitsweise von Computern arbeiten moderne kryptographische Verfahren nicht mehr mit ganzen Buchstaben, sondern mit den einzelnen Bits der Daten. Dies vergrößert die Anzahl der möglichen Transformationen erheblich und ermöglicht außerdem die Verarbeitung von Daten, die keinen Text repräsentieren. Moderne Krypto-Verfahren lassen sich in zwei Klassen einteilen: Symmetrische Verfahren verwenden wie klassische kryptographische Verfahren einen geheimen Schlüssel pro Kommunikationsbeziehung und für alle Operationen (z. B. Ver- und Entschlüsselung) des Verfahrens; asymmetrische Verfahren verwenden pro Teilnehmer einen privaten (d. h. geheimen) und einen öffentlichen Schlüssel. Fast alle asymmetrischen kryptographischen Verfahren basieren auf Operationen in diskreten mathematischen Strukturen, wie z. B. endlichen Körpern, Ringen, elliptischen Kurven oder Gittern. Ihre Sicherheit basiert dann auf der Schwierigkeit bestimmter Berechnungsprobleme in diesen Strukturen. Viele symmetrische Verfahren und (kryptologische) Hashfunktionen sind dagegen eher Ad-hoc-Konstruktionen auf Basis von Bit-Verknüpfungen (z. B. XOR) und Substitutions-Tabellen für Bitfolgen. Einige symmetrische Verfahren, wie z. B. Advanced Encryption Standard, Secret-Sharing oder Verfahren zur Stromverschlüsselung auf Basis linear rückgekoppelter Schieberegister, verwenden aber auch mathematische Strukturen oder lassen sich in diesen auf einfache Weise beschreiben.

Geschichte der Kryptographie

→ Hauptartikel: Geschichte der Kryptographie

Klassische Kryptographie

Der früheste belegte Einsatz von Kryptographie findet sich im dritten Jahrtausend v. Chr. in der altägyptischen Kryptographie des Alten Reiches. Hebräische Gelehrte benutzten im Mittelalter einfache Zeichentausch-Algorithmen (wie beispielsweise die Atbasch-Verschlüsselung). Im Mittelalter waren in ganz Europa vielfältige Geheimschriften zum Schutz des diplomatischen Briefverkehrs in Gebrauch, so etwa das Alphabetum Kaldeorum. Auch für heilkundliche Texte waren Geheimschriften in Gebrauch, etwa zur Niederschrift von Rezepten gegen die ab 1495 sich ausbreitende Syphilis.

Ende des 19. Jahrhunderts kam es aufgrund der weiten Verbreitung des Telegrafen (den man auf einfache Weise anzapfen und abhören konnte) zu neuen Überlegungen in der Kryptographie. So formulierte Auguste Kerckhoffs von Nieuwenhof mit Kerckhoffs’ Prinzip einen Grundsatz der Kryptographie, wonach die Sicherheit eines kryptographischen Verfahrens nur von der Geheimhaltung des Schlüssels und nicht von der des Verfahrens abhängen soll. Das Verfahren selbst kann vielmehr veröffentlicht und von Experten auf seine Tauglichkeit untersucht werden.

Kryptographie im Zweiten Weltkrieg

Markenschild der deutschen ENIGMA

Im Zweiten Weltkrieg wurden mechanische und elektromechanische Schlüsselmaschinen, wie T52 oder SZ 42, zahlreich eingesetzt, auch wenn in Bereichen, wo dies nicht möglich war, weiterhin Handschlüssel wie der Doppelkastenschlüssel verwendet wurden. In dieser Zeit wurden große Fortschritte in der mathematischen Kryptographie gemacht. Notwendigerweise geschah dies jedoch nur im Geheimen. Die deutschen Militärs machten regen Gebrauch von einer als ENIGMA bekannten Maschine, die ab 1932 durch polnische und ab 1939 durch britische Codeknacker gebrochen wurde.

Moderne Kryptographie

Beginn moderner Kryptographie

Das Zeitalter moderner Kryptographie begann mit Claude Shannon, möglicherweise dem Vater der mathematischen Kryptographie. 1949 veröffentlichte er den Artikel Communication Theory of Secrecy Systems. Dieser Artikel, zusammen mit seinen anderen Arbeiten über Informations- und Kommunikationstheorie, begründete eine starke mathematische Basis der Kryptographie. Hiermit endete auch eine Phase der Kryptographie, die auf die Geheimhaltung des Verfahrens setzte, um eine Entschlüsselung durch Dritte zu verhindern oder zu erschweren. Statt dieser – auch Security by obscurity genannten – Taktik müssen sich kryptografische Verfahren nun dem offenen wissenschaftlichen Diskurs stellen.

Data Encryption Standard (DES)

Die Feistelstruktur von DES

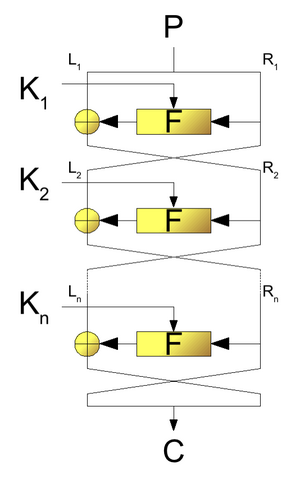
1976 gab es zwei wichtige Fortschritte. Erstens war dies der DES (Data Encryption Standard)-Algorithmus, entwickelt von IBM und der National Security Agency (NSA), um einen sicheren einheitlichen Standard für die behördenübergreifende Verschlüsselung zu schaffen (DES wurde 1977 unter dem Namen FIPS 46-2 (Federal Information Processing Standard) veröffentlicht). DES und sicherere Varianten davon (3DES) werden bis heute z. B. für Bankdienstleistungen eingesetzt. DES wurde 2001 durch den neuen FIPS-197-Standard AES ersetzt.

Asymmetrische Kryptosysteme (Public-Key-Kryptographie)

→ Hauptartikel: Asymmetrisches Kryptosystem

Der zweite und wichtigere Fortschritt war die Veröffentlichung des Artikels New Directions in Cryptography von Whitfield Diffie und Martin Hellman im Jahr 1976. Dieser Aufsatz stellte eine radikal neue Methode der Schlüsselverteilung vor und gab den Anstoß zur Entwicklung von asymmetrischen Kryptosystemen (Public-Key-Verfahren). Der Schlüsselaustausch war bis dato eines der fundamentalen Probleme der Kryptographie.

Vor dieser Entdeckung waren die Schlüssel symmetrisch, und der Besitz eines Schlüssels erlaubte sowohl das Verschlüsseln als auch das Entschlüsseln einer Nachricht. Daher musste der Schlüssel zwischen den Kommunikationspartnern über einen sicheren Weg ausgetauscht werden, wie beispielsweise durch einen vertrauenswürdigen Kurier oder beim direkten Treffen der Kommunikationspartner. Diese Situation wurde schnell unüberschaubar, wenn die Anzahl der beteiligten Personen anstieg. Auch wurde ein jeweils neuer Schlüssel für jeden Kommunikationspartner benötigt, wenn die anderen Teilnehmer nicht in der Lage sein sollten, die Nachrichten zu entschlüsseln. Ein solches Verfahren wird als symmetrisch oder auch als ein Geheimschlüssel-Verfahren (Secret-Key) oder Geteiltschlüssel-Verfahren (Shared-Secret) bezeichnet.

Bei einem asymmetrischen Kryptosystem wird ein Paar zusammenpassender Schlüssel eingesetzt. Der eine ist ein öffentlicher Schlüssel, der – im Falle eines Verschlüsselungsverfahrens – zum Verschlüsseln von Nachrichten für den Schlüsselinhaber benutzt wird. Der andere ist ein privater Schlüssel, der vom Schlüsselinhaber geheim gehalten werden muss und zur Entschlüsselung eingesetzt wird. Ein solches System wird als asymmetrisch bezeichnet, da für Ver- und Entschlüsselung unterschiedliche Schlüssel verwendet werden. Mit dieser Methode wird nur ein einziges Schlüsselpaar für jeden Teilnehmer benötigt, da der Besitz des öffentlichen Schlüssels die Sicherheit des privaten Schlüssels nicht aufs Spiel setzt. Ein solches System kann auch zur Erstellung einer digitalen Signatur genutzt werden. Die digitale Signatur wird aus den zu signierenden Daten oder ihrem Hashwert und dem privaten Schlüssel berechnet. Die Korrektheit der Signatur – und damit die Integrität und Authentizität der Daten – kann durch entsprechende Operationen mit dem öffentlichen Schlüssel überprüft werden. Public-Key-Verfahren können auch zur Authentifizierung in einer interaktiven Kommunikation verwendet werden.

Am 17. Dezember 1997 veröffentlichten die britischen Government Communications Headquarters (GCHQ) ein Dokument, in welchem sie angaben, dass sie bereits vor der Veröffentlichung des Artikels von Diffie und Hellman ein Public-Key-Verfahren gefunden hätten. Verschiedene als geheim eingestufte Dokumente wurden in den 1960er- und 1970er-Jahren u. a. von James H. Ellis, Clifford Cocks und Malcolm Williamson verfasst, die zu Entwürfen ähnlich denen von RSA und Diffie-Hellman führten.

Homomorphe Verschlüsselung

Ein homomorphes Verschlüsselungsverfahren erlaubt es, Berechnungen auf verschlüsselten Daten durchzuführen. Dem Kryptologen Craig Gentry gelang es 2009 nachzuweisen, dass ein Verschlüsselungsverfahren existiert, das beliebige Berechnungen auf verschlüsselten Daten zulässt. Eine homomorphe Verschlüsselung spielt eine wichtige Rolle beim Cloud-Computing. Um Datenmissbrauch bei der Verarbeitung sensibler Daten zu vermeiden, ist es wünschenswert, dass der Dienstleister nur auf den verschlüsselten Daten rechnet und die Klartexte nie zu Gesicht bekommt.

Kryptographie und Mathematik

Die Sicherheit der meisten asymmetrischen Kryptosysteme beruht auf der Schwierigkeit von Problemen, die in der algorithmischen Zahlentheorie untersucht werden. Die bekanntesten dieser Probleme sind die Primfaktorzerlegung und das Finden diskreter Logarithmen.

Faktorisierung

Die Sicherheit der faktorisierungsbasierten Public-Key-Kryptographie liegt in der Verwendung eines Produkts aus großen Primzahlen, welches als öffentlicher Schlüssel dient. Der private Schlüssel besteht aus den dazugehörenden Primfaktoren bzw. davon abgeleiteten Werten. Die Zerlegung einer hinreichend großen Zahl gilt aufgrund der sehr aufwendigen Faktorisierung als nicht praktikabel.

Beispiel zur Faktorisierung
Anschaulich gesprochen ist es trotz ausgefeilter Faktorisierungsverfahren schwierig, zu einer gegebenen Zahl, die das Produkt zweier großer Primfaktoren ist, z. B. der Zahl 805963, einen dieser Faktoren zu finden. Der Berechnungsaufwand zum Finden eines Faktors wächst dabei mit zunehmender Länge der Zahl sehr schnell, was bei genügend großen Zahlen dazu führt, dass die Faktorisierung auch auf einem Supercomputer tausende Jahre dauern würde. In der Praxis werden daher Zahlen mit mehreren hundert Dezimalstellen verwendet. Für die Multiplikation großer Zahlen existieren hingegen effiziente Algorithmen; es ist also leicht, aus zwei Faktoren (919 und 877) das Produkt (805963) zu berechnen. Diese Asymmetrie im Aufwand von Multiplikation und Faktorisierung macht man sich in bei faktorisierungsbasierten Public-Key-Verfahren zu Nutze. Kryptographisch sichere Verfahren sind dann solche, für die es keine bessere Methode zum Brechen der Sicherheit als das Faktorisieren einer großen Zahl gibt, insbesondere kann der private nicht aus dem öffentlichen Schlüssel errechnet werden.

Weitere Anwendungen der Zahlentheorie

Außer dem Faktorisierungsproblem finden sowohl das Problem des Diskreten Logarithmus (Elgamal-Kryptosystem) als auch fortgeschrittene Methoden der algebraischen Zahlentheorie, wie etwa die Verschlüsselung über elliptische Kurven (ECC) breite Anwendung.

Ein weiteres Anwendungsgebiet ist die Kodierungstheorie, die sich in ihrer modernen Form auf die Theorie der algebraischen Funktionenkörper stützt.

Zukünftige Entwicklungen

Siehe auch: Post-Quanten-Kryptographie

Die derzeit wichtigsten Public-Key-Verfahren (RSA), Verfahren, die auf dem Diskreten Logarithmus in endlichen Körpern beruhen (z. B. DSA oder Diffie-Hellman), und Elliptic Curve Cryptography könnten theoretisch durch so genannte Quantencomputer in Polynomialzeit gebrochen werden und somit ihre Sicherheit verlieren.

Kryptographie und Gesellschaft

In Zeiten des Internets wurde der Ruf auch nach privater Verschlüsselung laut. Bislang waren es Regierungen und globale Großunternehmen, die die RSA-Verschlüsselung aufgrund notwendiger, leistungsstarker Computer einsetzen konnten. Der amerikanische Physiker Phil Zimmermann entwickelte daraufhin eine RSA-Verschlüsselung für die breite Öffentlichkeit, die er Pretty Good Privacy (PGP) nannte und im Juni 1991 im Usenet veröffentlichte. Neu bei diesem Verfahren war die Möglichkeit, eine E-Mail mit einer digitalen Unterschrift zu unterzeichnen, die den Urheber der Nachricht eindeutig ausweist.

Kryptographie und Recht

Da es moderne, computergestützte Verfahren jedem möglich machen, Informationen sicher zu verschlüsseln, besteht seitens der Regierungen ein Bedürfnis, diese Informationen entschlüsseln zu können. Die US-Regierung prüfte im Jahr 1996, ob ein Verfahren gegen den Erfinder von PGP, Phil Zimmermann, wegen illegalen Waffenexports eingeleitet werden könne. Sie stellte das Verfahren jedoch nach öffentlichen Protesten ein. In den USA unterliegt Kryptographie, wie auch in vielen anderen Ländern, einem Exportbeschränkungsgesetz. In den USA regelt der Arms Export Control Act und die International Traffic in Arms Regulations den Export von Kryptographietechniken.

Oft gelingt Untersuchungsbehörden die Entschlüsselung eines Beweisstücks nur mit Hilfe des privaten Schlüssels. Es gibt in verschiedenen Ländern Mitwirkungspflichten bei der Entschlüsselung von Beweismaterial. Teilweise wird dabei auch vom Verdächtigten verlangt, den Schlüssel preiszugeben. In Großbritannien wurden Zuwiderhandlungen schon mit langen Haftstrafen geahndet. Nach Ansicht von Kritikern widerspricht dies dem Aussageverweigerungsrecht.

In Frankreich gab es von 1990 bis 1996 ein Gesetz, das zum Deponieren dieses Schlüssels bei einer „vertrauenswürdigen Behörde“ verpflichtete. Damit verbunden war ein Verbot anderer Verfahren und Schlüssel. Einem Journalisten, der dies praktizieren wollte, ist es allerdings nicht gelungen, eine dafür zuständige Behörde zu finden. Nach einer Lockerung des Gesetzes 1996 ist die Verwendung bestimmter Kryptographieverfahren genehmigungspflichtig. Auch in Deutschland und in der EU gibt es seit Jahren Debatten über gesetzliche Kontrolle der Kryptographie. Ein Verbot der Kryptographie ist nicht praktikabel, da die Algorithmen bekannt sind und jeder mit den notwendigen Programmierkenntnissen ein entsprechendes Programm selbst schreiben könnte. Web-Anwendungen wie z. B. elektronisches Banking oder Shopping sind ohne Kryptographie nicht denkbar.

Im Rahmen der digitalen Rechteverwaltung werden Kryptographieverfahren eingesetzt, deren Umgehung (mittels Kryptoanalyse) unter Strafe gestellt ist.

Siehe auch

• CrypTool – Lernsoftware zum Thema Kryptographie und Kryptoanalyse, Open-Source
• Kleptographie
• Molekularer Schlüssel

Literatur

• Friedrich L. Bauer: Entzifferte Geheimnisse. Methoden und Maximen der Kryptologie. Dritte, überarbeitete Auflage, Springer, Berlin 2000, ISBN 3-540-67931-6
• Albrecht Beutelspacher, Jörg Schwenk, Klaus-Dieter Wolfenstetter: Moderne Verfahren der Kryptographie. Vieweg 2004, ISBN 3-528-36590-0
• Albrecht Beutelspacher: Geheimsprachen, C.H. Beck, München 2005, ISBN 3-406-49046-8
• Johannes Buchmann: Einführung in die Kryptographie. Springer 2003, ISBN 3-540-40508-9
• Wolfgang Ertel: Angewandte Kryptographie. Hanser 2003, ISBN 3-446-22304-5
• Niels Ferguson, Bruce Schneier, Tadayoshi Kohno: Cryptography Engineering: Design Principles and Practical Applications. John Wiley & Sons 2010, ISBN 978-0-470-47424-2
• David Kahn: The Codebreakers: The Comprehensive History of Secret Communication from Ancient Times to the Internet. Scribner, New York, Auflage Rev Sub, 1996. ISBN 978-0-684-83130-5
• Christian Karpfinger, Hubert Kiechle: Kryptologie – Algebraische Methoden und Algorithmen. Vieweg+Teubner 2010, ISBN 978-3-8348-0884-4
• Heiko Knospe: A Course in Cryptography. American Mathematical Society, Pure and Applied Undergraduate Texts, Volume: 40, 2019. ISBN 978-1-4704-5055-7
• Jörn Müller-Quade: Hieroglyphen, Enigma, RSA – Eine Geschichte der Kryptographie. Fakultät für Informatik der Universität Karlsruhe. Abgerufen: 28. Mai 2008. ira.uka.de (PDF; 2,1 MB)
• Christof Paar, Jan Pelzl: Understanding Cryptography: A Textbook for Students and Practitioners. Springer, 2009, ISBN 978-3-642-04100-6
• Para: Geheimschriften, Otto Maier Verlag GmbH, Ravensburg 1994, ISBN 978-3-473-51662-9.
• Norbert Pohlmann: Cyber-Sicherheit: Das Lehrbuch für Konzepte, Prinzipien, Mechanismen, Architekturen und Eigenschaften von Cyber-Sicherheitssystemen in der Digitalisierung. Springer Vieweg, September 2019, ISBN 3658253975
• Klaus Schmeh: Codeknacker gegen Codemacher. Die faszinierende Geschichte der Verschlüsselung. 2. Auflage. Verlag: W3l, 2007, ISBN 978-3-937137-89-6
• Klaus Schmeh: Kryptografie – Verfahren, Protokolle, Infrastrukturen. 5. Auflage. dpunkt, 2013, ISBN 978-3-86490-015-0
• Bruce Schneier: Angewandte Kryptographie. Addison-Wesley 1996, ISBN 3-89319-854-7
• Bruce Schneier, Niels Ferguson: Practical Cryptography. Wiley, Indianapolis 2003. ISBN 0-471-22357-3
• Simon Singh: Geheime Botschaften. Die Kunst der Verschlüsselung von der Antike bis in die Zeiten des Internet. dtv 2001, ISBN 3-423-33071-6
• Fred B. Wrixon: Codes, Chiffren & andere Geheimsprachen. Könemann 2001, ISBN 3-8290-3888-7
• Kryptographie. Spektrum der Wissenschaft, Dossier 4/2001
• Wenbo Mao: Modern Cryptography. Theory and Practice. Prentice Hall 2004, ISBN 0-13-066943-1
• Andreas Pfitzmann: Scriptum „Sicherheit in Rechnernetzen: Mehrseitige Sicherheit in verteilten und durch verteilte Systeme“ (Memento vom 29. Juni 2007 im Internet Archive), englische Version (Memento vom 25. März 2009 im Internet Archive)
• Christian Reder: Wörter und Zahlen. Das Alphabet als Code, Springer 2000, ISBN 3-211-83406-0
• B. L.: Etwas über Geheimschrift. In: Die Gartenlaube. Heft 14, 1882, S. 234–236 (Volltext [Wikisource]). 

Weblinks

Commons: Kryptographie – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Kryptografie – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Reinhard Wobst: „Harte Nüsse – Verschlüsselungsverfahren und ihre Anwendungen“, Heise Security 2003
• Interessante Einführung in die Materie (auch Bauanleitungen für Chiffriergeräte) (Memento vom 7. Oktober 2010 im Internet Archive)
• Eine Einführung in die Anwendung der Verschlüsselung
• Überblick und Geschichte der Kryptologie
• Allgemeinverständlicher Podcast zu den Grundlagen der Kryptographie
• Videos einer zweisemestrigen Vorlesung Einführung in die Kryptographie von Christof Paar, Uni Bochum (Videos sind in Deutsch)
• Information Security Encyclopedia intypedia
• Lucia Schaub: Geheimschrift. In: ZEITmagazin. Rubrik Wundertüte. Nr. 10/2016, 18. März 2016, abgerufen am 20. Mai 2016 (für Kinder).
• Geheimschriften und Sprachen für Kinder: 1337 Leet, Winkelschrift, Lefu-Sprache, Hieroglyphen u. a. In: labbe.de/zzzebra, abgerufen am 20. Mai 2016.