Metcalfesches Gesetz
Das Metcalfesche Gesetz (englisch Metcalfe's law) gehört zur Netzwerkökonomie und beschreibt in Netzwerken einen positiven Netzwerkeffekt, wonach sich der Nutzwert insbesondere sozialer Netzwerke im Vergleich zur Anzahl seiner Benutzer verdoppele, während die Kosten nur linear zur Teilnehmerzahl steigen.
Allgemeines
Außerhalb der Rechtswissenschaft (formales Gesetz) spricht man in den Wissenschaften von einem Gesetz, wenn aus Beobachtungen orts- und zeitunabhängige allgemeingültige Aussagen abgeleitet und zu einer Theorie verdichtet werden, die weltweit dauerhaft, aber nicht immer ausnahmslos, gilt. Naturgesetze sind in der Naturwissenschaft dagegen ausnahmslos geltende Regeln für den Ablauf des Geschehens.[1] Das Metcalfesche Gesetz beruht auf Beobachtungen, die durch Induktion verallgemeinert wurden und deshalb nicht ausnahmslos gelten können; es gehört damit zu den empirischen Gesetzen.
Entstehung
Das Metcalfesche Gesetz ist benannt nach dem Erfinder des Ethernet, Robert Metcalfe. Er erkannte 1980, dass der Wert eines Telekommunikationsnetzes sich proportional zum Quadrat der Anzahl verbundener Endgeräte entwickele, veröffentlichte diese Erkenntnis jedoch nicht.[2] Diese blieb deshalb unbeachtet, so dass erst George Gilder im Jahre 1993 hierauf hinwies,[3] die Formulierung Metcalfe zuschrieb und die Endgeräte durch Benutzer ersetzte.[4]
Mathematische Darstellung
Das Metcalfesche Gesetz geht davon aus, dass jede Art von Netzwerk (wie Internet, Rechnernetzwerk oder soziales Netzwerk) einen Nutzwert aufweist, welcher der Quadratzahl der Anzahl seiner Mitglieder entspricht. Für jede Anzahl von Netzteilnehmern kann der potenzielle Nutzwert des Netzwerks mit
beschrieben werden.[5] Jeder Teilnehmer kann Verbindungen aufbauen, so dass das gesamte Netzwerk einen Wert von , also knapp aufweist.
Das Gesetz besagt, dass der Nutzen eines Netzwerks gleich entspricht, allerdings wird dieser Term zu bei großen Netzwerken approximiert, so dass der Wert eines Netzwerks quadratisch mit der Anzahl der Nutzer steigt.[6]
- (für große n).
Während der Nutzen proportional zum Quadrat der Anzahl der möglichen Verbindungen wächst, steigen die Kosten proportional zur Teilnehmerzahl an. Das Metcalfesche Gesetz erklärt einige der Netzwerkeffekte von Kommunikationstechniken wie z. B. im Bereich des Internets, Telefons oder Faxgeräts. Ein einzelnes Faxgerät ist nutzlos. Mit jedem weiteren Gerät im Netzwerk steigt die Möglichkeit der Interaktion und damit auch der Nutzen dieser Kommunikationstechnologie.
Vergleich
Geht man von Benutzern eines Netzwerks aus, so wird sein Wachstum – je nach dem zugrunde gelegten Gesetz – zwischen einem Benutzer () und sechs Benutzern zu folgenden Wertentwicklungen führen:[7]
| Gesetz | Wert ( Teilnehmer) | 1 | 2 | 3 | 4 | 5 | 6 | Beispiele |
|---|---|---|---|---|---|---|---|---|
| Sarnoff-Gesetz | N | 1 | 2 | 3 | 4 | 5 | 5 | Radio, Fernsehen |
| Metcalfesches Gesetz | N2 | 1 | 4 | 9 | 16 | 25 | 36 | Telefonnetz, E-mail |
| Reedsches Gesetz | 2N | 0 | 1 | 4 | 11 | 26 | 57 | soziale Netzwerke, Chat-Foren |
| n*log(n) | n*log(n) | 0 | 0,602059991 | 1,431363764 | 2,408239965 | 3,494850022 | 4,668907502 |
Sarnoffs Gesetz entstand 1920 und ist benannt nach David Sarnoff, dem damaligen Chef der Radio Corporation of America (RCA). Er ging davon aus, dass sich der Unternehmenswert einer Rundfunkanstalt proportional zur Anzahl ihrer Hörer oder Zuschauer entwickele, weil Rundfunk eine einseitige Kommunikation ermögliche (von einem Sender an viele Empfänger; englisch one-to-many) und somit einen Wert von besitzt. Das Reedsche Gesetz aus 1999 stellt eine Erweiterung des Metcalfeschen Gesetzes dar. Beide sind Netzwerke, wo viele mit vielen Teilnehmern verbunden sind (englisch many-to-many).
Anwendungsgebiete
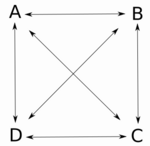
Bei zwei Teilnehmern eines Kommunikationsnetzes ( und Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle B} ) bestehen zwei Verbindungen, von Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle A} nach Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle B} und umgekehrt. Kommt ein weiterer Nutzer Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle C} hinzu, steigt die Anzahl der Verbindungen auf sechs an für Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n=3} gilt Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle 3(3-1)=6} . Bei einem Netzwerk mit 3 Teilnehmern (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle n = 3} ) steigt der Nutzwert auf (Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle U = 9} ), weil jeder Teilnehmer mit jedem anderen Teilnehmer in Verbindung treten kann. Der Nutzwert des Netzwerks erhöht sich mit quadratischem Wachstum bei lediglich linear wachsender Mitgliederzahl.
Seit den 1990er Jahren, in denen mehrere westliche Armeen eine Transformation einläuteten, hat das Gesetz in deren kommunikationstechnische Vernetzung Einzug gehalten. Bei der in dieser Hinsicht führenden Armee, den US-Streitkräften, findet das Gesetz in der netzwerkorientierten Kriegsführung Eingang.
Wirtschaftliche Aspekte
Das Metcalfesche Gesetz beschreibt einen Teilbereich des positiven, direkten Netzwerkeffekts, bei dem große Netzwerke attraktiver für Benutzer sind und somit einen Wettbewerbsvorteil gegenüber kleineren Netzwerken darstellen. Metcalfe selbst hat die Auswirkung dieses Netzwerkeffektes stark eingeschränkt. Für ihn gilt dieses „Gesetz“ nur solange, bis die kritische Masse (englisch Tipping-Point) im Netzwerk erreicht ist. Diese Klarstellung erschien im Jahre 2006.[8] Nur dann gilt in der Netzwerkökonomie, dass der Nutzen die Kosten des Netzwerks übersteigt. Allerdings bezweifeln die zitierten Autoren die entscheidende Annahme, dass der Nutzen tatsächlich proportional zum Quadrat der Anzahl der Teilnehmer wächst. Konkurrieren zwei oder mehr Wettbewerber in einem Netzmarkt mit starken positiven Feedback-Effekten, wird einer als Marktführer aufsteigen, während die anderen wahrscheinlich nicht überleben werden.[9]
Wird dagegen die kritische Masse überschritten, ergeben sich durch eine überhöhte Netzlast negative Netzwerkeffekte. Wenn beispielsweise das Rechnernetz mit zu hohen Datenmengen belastet wird, kommt es zur Überlastung der Server mit der Folge längerer Antwortzeiten. Wird das Straßennetz durch steigende Verkehrsdichte stark beansprucht (etwa zur Hauptverkehrszeit), gibt es Verkehrsstaus, die unter anderem Verspätungen zur Folge haben.
Das Metcalfsche Gesetz zeigt ein überproportionales Wachstum, wenn die Benutzer-Zahlen steigen. Autoren gingen deshalb davon aus, dass die im März 2000 geplatzte Internetblase zurückzuführen war auf vorgenommene Erweiterungsinvestitionen im Hinblick auf die Vergrößerung eines Netzwerks, die nicht den Gewinnchancen entsprachen (beispielsweise bei AOL). Der fundamentale Fehler im Metcalfeschen Gesetz ist die Grundannahme, dass sowohl jegliche Verbindung als auch jegliche Gruppe denselben maximalen Wert besitzt.[10] Denn manche Kommunikationsverbindungen werden häufiger benutzt als andere, so dass diese Annahme nicht der Realität entspricht.
Einzelnachweise
- ↑ Max Apel/Peter Ludz, Philosophisches Wörterbuch, 1958, S. 110; ISBN 9783110067293
- ↑ Bob Metcalfe, Metcalfe's Law Recurses Down the Long Tail of Social Networks, in: VCMike's Blog, 2006, S. 1
- ↑ George Gilder, Metcalfe's Law and Legacy, in: Forbes ASAP, September 1993, S. 158
- ↑ Roberto Moro Visconti, The Valuation of Digital Intangibles, 2020, S. 185
- ↑ Frank S. Backa, Markteinführungsstrategie für Virtual-Reality-Brillen: Erfolg durch die Nutzung von Netzwerkeffekten, 2017, S. 36 ff.
- ↑ Carl Shapiro/Hal R. Varian, Information Rules: A Strategic Guide to the Network Economy, in: Harvard Business School Press, 1999, S. 184: englisch „[…] the value of a network goes up as a square of the number of users“.
- ↑ Frank S. Backa, Markteinführungsstrategie für Virtual-Reality-Brillen: Erfolg durch die Nutzung von Netzwerkeffekten, 2017, S. 39
- ↑ Bob Briscoe/Andrew Odlyzko/Benjamin Tilly, Metcalfe's law is wrong, in: IEEE Spectrum Magazine vol. 43, Juli 2006, S. 34 – 39
- ↑ Carl Shapiro/Hal R. Varian, Information Rules: A Strategic Guide to the Network Economy, in: Harvard Business School Press, 1999, S. 184
- ↑ Frank S. Backa, Markteinführungsstrategie für Virtual-Reality-Brillen: Erfolg durch die Nutzung von Netzwerkeffekten, 2017, S. 40