Polygenie

aus Wikipedia, der freien Enzyklopädie
(Weitergeleitet von Multifaktorieller Erbgang)

Polygenie (aus dem Altgriechischen abgeleitet für vielfache Abstammung, englisch polygene meist als polygenic nur als Adjektiv gebraucht) ist ein Begriff aus der Genetik. Er wird für Fälle verwendet, in denen die im jeweiligen Interesse stehende Ausprägung eines Merkmals des Phänotyps, zum Beispiel eine Erbkrankheit, von mehr als einem einzelnen Gen abhängt. Kann die beobachtete Merkmalsverteilung durch genetische Unterschiede, genannt verschiedene Allele, an einem einzelnen Genlocus erklärt werden, spricht man im Gegensatz dazu von Monogenie.

Wie ein einzelnes Merkmal sehr oft von verschiedenen Genen abhängen kann, kommt es verbreitet ebenso vor, dass ein einzelnes Gen (eigentlich: ein Allel eines Gens) verschiedene Merkmale gleichzeitig beeinflusst, dies wird dann auf das Gen bezogen Pleiotropie oder, bezogen auf das Merkmal selbst, Polyphänie genannt. Vereinfacht kann daher gesagt werden: Polygenie: ein Merkmal, verschiedene Gene; Polyphänie (oder Pleiotropie): ein Gen, verschiedene Merkmale.

In der klassischen formalen Genetik (auch mendelsche Genetik) sind Erbgänge, die durch die Interaktion verschiedener Gene geprägt sind, schwierig zu untersuchen, weil die Merkmalsverteilung bei ihnen nicht der dritten Mendelschen Regel (Unabhängigkeitsregel) folgt. Sind nur wenige Gene betroffen, lässt sich die Merkmalsverteilung in Kreuzungsexperimenten meist noch auf eine zwar größere, aber überschaubare Reihe ergänzender Regeln zurückführen, die die Form dieser Interaktionen berücksichtigt. Sind – wie bei den meisten realen Merkmalen – viele oder sehr viele Gene an der Merkmalsausprägung beteiligt, versagt dieser Forschungsansatz ganz. Diese Merkmale werden „quantitative“ (auch komplexe oder additive) Merkmale genannt. Nach einem auf Ronald Aylmer Fisher zurückgehenden Forschungsansatz erfolgt ihre Untersuchung mit statistischen Methoden, die Forschungsrichtung wird quantitative Genetik genannt. Die Untersuchung polygener Merkmale entspricht also in etwa dem Bereich der quantitativen Genetik, diejenige monogener Merkmale der mendelschen Genetik. Merkmale, die von einer überschaubaren Anzahl von Genen beeinflusst werden, fallen in eine Grauzone, in der beide Ansätze konkurrierend eingesetzt werden können. Diese wurden klassisch ebenfalls polygen genannt, heute hat sich dafür stattdessen der Ausdruck „oligogen“ durchgesetzt.[1] Genetiker sprechen heute also, im Gegensatz zu den Pioniertagen der Genetik, von Polygenie meist nur noch für quantitative Merkmale, die von einer großen (oft nicht abzählbaren) Zahl von Genen abhängen.[2]

Abgrenzung

Polygenie liegt dann vor, wenn ein einzelnes Merkmal von mehreren Genen beeinflusst wird. Dieser Einfluss kann sich in verschiedener Art äußern.

Epistase

In seinen klassischen Experimenten an Erbsen hatte Gregor Mendel für die von ihm untersuchten sieben Merkmale (der Wuchsform, der Farbe und Oberflächengestalt der Samen und der Blütenfarbe) bei der Erbse herausgefunden, dass die Merkmalsausprägungen voneinander unabhängig vererbt werden. Für jedes dieser Merkmale postulierte er eine später Gen genannte Erbanlage, von der jeweils ein Satz vom Vater bzw. von der Mutter an die Nachkommen weitergegeben (vererbt) wird.[3] Der Variabilität der Merkmale in seinen Versuchen, bei denen jedes Merkmal in zwei, qualitativ unterschiedlichen, Ausprägungen auftrat, lag also pro Merkmal jeweils nur ein einzelnes Gen zugrunde. Interaktionen dieser Gene traten nicht auf, oder waren zumindest vernachlässigbar klein. Die meisten für Forscher interessanten Merkmale, und ihre Gene, verhalten sich allerdings anders (so dass anzunehmen ist, dass Mendel seine Versuchsobjekte sorgfältig und nach entsprechenden Vorversuchen auswählte). Solche Wechselwirkungen zwischen Genen werden allgemein Epistase genannt. (Zu beachten ist dabei unbedingt: Der Ausdruck wurde in der Mendelschen Genetik ursprünglich durch William Bateson ausschließlich für Fälle definiert, bei denen der Einfluss eines Genlocus auf den Phänotyp durch den Einfluss eines zweiten völlig überdeckt (maskiert) wurde; heute wird er auch für alle anderen Fälle verwendet, bei denen irgendeine Beziehung zwischen zwei Genloci sich auf den Phänotyp auswirkt.[4]) Liegt Epistase vor, hängt der Einfluss eines Gens auf das untersuchte Merkmal also neben dem Vorliegen des jeweils betrachteten Allels an diesem Genlocus, also von dem genetischen Polymorphismus, auch von einem (oder mehreren) anderen Genen ab.

Kopplung, Haplotypen, Linkage Disequilibrium

Betrachtet man die Vererbung von Merkmalen, die polygen vererbt werden, zeigt es sich häufig, dass bestimmte Merkmale häufiger gemeinsam auftreten, als es bei zufälliger, unabhängiger Vererbung zu erwarten wäre (wie sie etwa die dritte Mendelsche Regel unterstellt). In der Genetik wird hier von Kopplung dieser Merkmale, bzw. der sie hervorrufenden Gene, gesprochen. In den frühen Tagen der Genetik gelang es Forschern durch geduldiges Protokollieren vieler Kreuzungsexperimente, Gruppen von Genen herauszufinden, die häufig miteinander gekoppelt vererbt werden. Solche „Kopplungsgruppen“ entsprechen in der Regel den verschiedenen Chromosomen. Kopplung kann durch Crossing-over während der Meiose aufgebrochen werden, in dem homologe DNA-Abschnitte zwischen väterlichen und mütterlichen Chromosomen des diploiden Chromosomensatzes ausgetauscht werden. Dies geschieht, für einzelne Genpaare betrachtet, aber nur sehr selten. Mittels Kopplungsanalyse können Genetiker die Genkopplung anhand der phänotypischen Merkmalsverteilung untersuchen.[5] Heute werden aber in vielen Fällen unbekannte Gene mittels in Genbanken hinterlegter bekannter Sequenzen direkt zugeordnet, die Technik wird Genomweite Assoziationsstudie, abgekürzt GWAS, genannt. Genkopplung bei polygen vererbten Merkmalen wirkt sich überhaupt nicht auf den einzelnen Phänotyp aus. Lediglich dessen Verteilung und Häufigkeit ist anders als erwartet.

Allele von Genen, die auf demselben Chromosomen sitzen, sind also miteinander gekoppelt und werden im Regelfall gemeinsam vererbt, da ja bei der Meiose, ohne Crossing-over-Effekte, nur die haploiden Chromosomensätze neu verteilt werden. Sitzen die Allele hingegen auf verschiedenen Chromosomen, besitzt ihre gemeinsame Vererbung nur eine Wahrscheinlichkeit von 50 Prozent. Wegen dieser Bedeutung wurde für die gemeinsam vorkommenden Gene ein neuer Fachausdruck eingefügt: Haplotyp. Beim menschlichen Genom ist inzwischen bekannt, das große Abschnitte innerhalb eines Chromosoms fast immer blockweise vererbt werden, es kommt hier innerhalb der Blöcke fast nie zum Crossing-over. Durch diese Haplotyp-Blöcke bleiben Haplotypen oft über viele Generationen unverändert erhalten. Ihre Analyse besitzt große Bedeutung, unter anderem für die Enträtselung der individuellen Abstammung von Einzelpersonen und Populationen.

Der Ausdruck Linkage disequilibrium (übersetzt in etwa „Genkopplungs-Ungleichgewicht“, wird aber meist als Fachterminus nicht mehr übersetzt) geht auf die Ergebnisse von Kopplungsanalysen zurück. Heute wird dieser Ausdruck allerdings in einem erweiterten Sinne für alle Assoziationen verschiedener Allele im Genom miteinander gebraucht, deren Verteilung von der Zufallsverteilung abweicht, wobei es gleichgültig ist, ob diese auf Kopplung zurückgeht oder nicht; die Verwendung des Ausdrucks dafür hat nur noch historische Gründe.[6] Linkage disequilibrium, also das nicht-zufällige gemeinsame Auftreten verschiedener Allele, kann innerhalb von Populationen und zwischen Populationen berechnet werden. Es ist zunächst unabhängig davon, ob die so gekoppelten Sequenzabschnitte oder Gene tatsächlich auf ein bestimmtes Merkmal gemeinsam einwirken, also Polygenie vorliegt. Dies ist aber häufig der Fall und stellt einen wichtigen Forschungsansatz dar, um das herauszufinden.

Auch Linkage disequilibrium und Epistase stehen in keinem direkten sachlichen Zusammenhang, linkage disequilibrium beeinflusst lediglich die Häufigkeitsverteilung eines polygenen Merkmals in einer untersuchten Population, nicht die genetische Basis dieses Merkmals selbst.

Additive Polygenie

Bei der additiven Polygenie wirken verschiedene Gene bei der Ausbildung eines Merkmals zusammen und addieren sich in ihrer Wirkung. Sind viele Gene an der Ausprägung des interessierenden Merkmals beteiligt, ergibt sich für dieses eine lückenlose Abfolge (keine Segregation der Merkmale), zum Beispiel beim Merkmal Körpergröße nicht zwei, drei oder mehr diskrete Größenklassen, sondern ein stufenlos variierendes Spektrum vom kleinsten bis zum größten Individuum. Dieses folgt in der Gesamtverteilung einer Gauß-Kurve. Die Gesamtvarianz ergibt sich ebenfalls additiv aus den Teilvarianzen der jeweiligen Einzelgene. Merkmale, die diesem Profil entsprechen, werden von den Genetikern „quantitative“ Merkmale genannt. Meist wird der Begriff Polygenie heute ausschließlich auf diese bezogen. Obwohl die verschiedenen Allele an den unterschiedlichen, an der Merkmalsausprägung beteiligten Genloci, jedes für sich betrachtet, in ihrer Verteilung den Mendelschen Regeln folgend ausgeprägt sein können, ergibt sich für viele Gene insgesamt eine stufenlose und kontinuierliche Verteilung. Auch Epistase zwischen einzelnen Genen ändert normalerweise nichts an der Verteilung, da sich der Nettoeffekt der Epistase in den meisten Zusammenhängen genauso auswirkt wie ein entsprechendes Gen mit tatsächlich additiver Wirkung („apparente“ additive Varianz).[4] Bei quantitativen Merkmalen geht immer der klare Zusammenhang zwischen Gen und Merkmal verloren. Im Bezugsrahmen der formalen Genetik spricht man von unvollständiger Penetranz, d. h. auch bei einem dominanten Gen zeigen nicht alle Individuen, die Träger des entsprechenden Allels sind, das phänotypische Merkmal. Im Falle von Krankheiten kann nicht mehr der Ausbruch der Krankheit vorhergesagt werden, sondern nur ein, mehr oder weniger großes, Risiko (medizinisch: eine Disposition) dafür. Außerdem kann derselbe Phänotyp (also hier: die Krankheit) bei verschiedenen Patienten auf ganz unterschiedliche Kombinationen von Genen zurückgehen.

Die einzelnen Komponenten der additiven Polygenie werden mit dem englischsprachigen Fachausdruck Quantitative Trait Locus, meist abgekürzt als QTL, bezeichnet. Typischerweise addieren sich allerdings die bei der QTL-Analyse gefundenen Komponenten oft nicht zur Gesamt-Heritabilität (Erblichkeit) auf. Worauf diese Diskrepanz beruht, ist wissenschaftlich immer noch umstritten. Eine plausible Antwort wäre auch hier ein epistatischer Effekt, der sich aus der Interaktion von Gen-Netzwerken ergibt, darauf deuten Studien an Modellorganismen hin.

Die additive Polygenie (der Ausdruck geht auf englische biometrische Forscher wie Kenneth Mather zurück) wurde in den deutschsprachigen Ländern lange Zeit mit dem synonymen Ausdruck Polymerie bezeichnet. Einige differenzierten weiter und bezeichneten mit Homomerie die additive Wirkung gleich stark wirkender, mit Heteromerie (oder auch Polymerie im engeren Sinne) das Zusammenwirken von Faktoren verschiedener Stärke.[7][8] Grundlage waren vor allem die 1909 publizierten klassischen Experimente zur Körnerfarbe von Hafer und Weizen, des Pflanzengenetikers Herman Nilsson-Ehle (1873–1949)[9]

Polygenie und Umwelteinflüsse (multifaktorielle Vererbung)

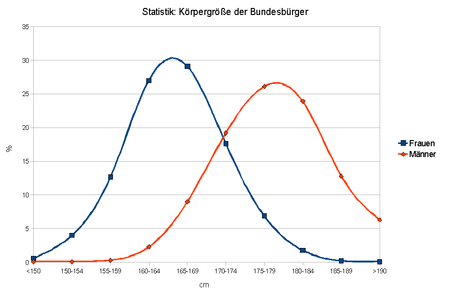
Statistik der Körpergrößen als Diagramm. Die tatsächliche Körpergröße einer Person wird sowohl von den Genen als auch der Umwelt beeinflusst. Nimmt man alle Personen einer Population, so zeigt sich ein regelmäßiges Muster: die Normalverteilung.

Ist ein Merkmal sowohl von mehreren Genen als auch von Umweltfaktoren abhängig, spricht man von multifaktorieller Vererbung.[10] Viele Genetiker wollen den Begriff polygene Vererbung auf Fälle beschränken, bei denen die Merkmalsvarianz ausschließlich genetisch determiniert ist, also Einflüsse der Umwelt sollen ausgeschlossen werden; dies wird aber im tatsächlichen Sprachgebrauch oft nicht beachtet.[11]

Bei Betrachtung einer ganzen Population im Hinblick auf ein quantitatives Merkmal führt das Zusammenspiel von Polygenie und Umweltfaktoren zu einer kontinuierlichen Varianz des Phänotyps (innerhalb eines bestimmten Rahmens). Je mehr Gene beteiligt sind, desto kontinuierlicher wird die Kurve. Die kontinuierliche Variabilität (sowohl einzeln durch Polygenie bzw. Umweltfaktoren beeinflusst, als auch im Zusammenspiel dieser entstanden) führt zu einem Verteilungsmuster, das dem der Gauß-Kurve entspricht. Insgesamt folgen viele menschliche Eigenschaften (IQ, Körpergröße, Gewicht) der Normalverteilung.[12]

Beispiele

Die Hautfarbe. An der Ausprägung der Hautpigmentierung des Menschen sind zahlreiche, möglicherweise Hunderte, Gene, beteiligt.[13] Das ermöglicht eine sehr weite Abstufung zwischen sehr dunkler und sehr heller Hautfarbe. Umwelteinflüsse wie die UV-Strahlung verändern den Phänotyp der Haut zusätzlich. Dabei wird in der Haut die Produktion von Melanin innerhalb genetisch festgelegter Grenzen zusätzlich angeregt und die Haut erscheint dunkler. Auch diese Reaktionsnorm besitzt eine genetische Basis.

Die Körpergröße. Zunächst wird sie in einem gewissen Rahmen vererbt. Das heißt, große Eltern bekommen in der Regel große Kinder. Die tatsächlich erreichte Größe hängt aber zusätzlich von der Qualität der Ernährung des Menschen ab; vor allem von der reichlichen Zufuhr von Eiweiß ab. Dabei begrenzt die individuelle genetische Konstitution jedoch die Größe auf ein Höchstmaß.

Komplementäre Polygenie

In einem klassischen Experiment im Jahr 1905 fanden William Bateson und Reginald Punnett, dass bei der Kreuzung zweier rein weiß blühender Sorten der Duftenden Platterbse (Lathyrus odoratus) auch violett blühende Nachkommen auftraten.[14] Die Segregation der Merkmale weicht dabei von den nach der dritten Mendelschen Regel zu erwartenden Verhältnissen ab. Sie konnten zeigen, dass das Ergebnis durch das Zusammenspiel zweier Gene erklärt werden kann, bei der das Merkmal nur dann auftritt, wenn ein bestimmtes, dominantes Allel bei beiden Genen ausgeprägt ist. Wenn die Allele A und B der beiden Gene für violett blühende und ihre Mutanten a und b für weiß blühende Blüten kodieren, wird violett nur ausgeprägt, wenn zumindest ein Allel A und ein B im Erbgut vorhanden sind (Kombination A_B_, z. B. AaBb, AABb, AaBB usw.). In den ursprünglichen Sorten kann die Ausprägung AAbb und aaBB rekonstruiert werden, die beide weiße Blüten ergeben. Betrachtet man alle möglichen Kombinationen, ergibt sich ein Verhältnis von 9 zu 7 für die violett blühende Variante, d. h. sieben Kombinationen ergeben violette, neun weiße Blüten.[15] Für solche Verhältnisse, bei denen ein Phänotyp von der Interaktion von zwei Genen abhängt, die einander ergänzen, wurde der Ausdruck komplementäre Polygenie eingeführt. Heute weiß man, dass die genetische Grundlage dafür meist Ketten oder Kaskaden hintereinander geschalteter Gene sind, die versagen, wenn ein beliebiges Glied der Kette ausfällt.[16] Nach dem „Dobzhansky-Muller-Modell“ (tatsächlich zuerst vorgeschlagen von Bateson) können komplementäre Gene eine wichtige Rolle bei der Artbildung spielen, in dem sie die, ansonsten unplausible, Entstehung der Sterilität von Hybriden zwischen den neu entstandenen Arten ermöglichen.[17]

Komplementäre Gene gelten heute als ein Beispiel für Epistase. Sie werden, im Gegensatz zum früheren Sprachgebrauch, nicht mehr unter den Begriff Polygenie gefasst. Der frühere Sprachgebrauch ist in vielen älteren Werken, darunter auch Schulbücher und Prüfungsunterlagen, aber noch zu finden.

Einzelnachweise

  1. ↑ R. Rieger,A. Michaelis,M.M. Green: Glossary of Genetics and Cytogenetics: Classical and Molecular. Springer Verlag, 4. Auflage 2012. ISBN 978-3-642-96327-8. auf Seite 74.
  2. ↑ vgl. „polygene: one of a group of genes that together control a quantative character.“ (Eines einer Gruppe von Genen, die gemeinsam ein quantitatives Merkmal kontrollieren). in: Robert C. King, William D. Stansfield, Pamela K. Mulligan: A Dictionary of Genetics. Oxford University Press, siebte Auflage 2006. ISBN 978-0-19-530762-7.
  3. ↑ zur molekularen Identität der klassischen Mendelschen Gene vgl. James B. Reid & John J. Ross (2011): Mendel’s Genes: Toward a Full Molecular Characterization. Genetics 189 (1): 3-10. doi:10.1534/genetics.111.132118
  4. ↑ a b Trudy F. C. Mackay (2014): Epistasis and quantitative traits: using model organisms to study gene–gene interactions. Nature Reviews Genetics 15: 22-33. doi:10.1038/nrg3627
  5. ↑ Jurg Ott, Jing Wang, Suzanne M. Leal (2015): Genetic linkage analysis in the age of whole-genome sequencing. Nature Reviews Genetics 16(5): 275–284. doi:10.1038/nrg3908
  6. ↑ Montgomery Slatkin (2008): Linkage disequilibrium — understanding the evolutionary past and mapping the medical future. Nature Reviews Genetics 9: 477-485. doi:10.1038/nrg2361
  7. ↑ Julius Bauer: Vorlesungen über allgemeine Konstitutions- und Vererbungslehre für Studierende und Ärzte. Julius Springer Verlag, Berlin, zweite Auflage 1923. darin sechste Vorlesung: Die experimentell-biologischen (Mendelschen) Vererbungsgesetze.
  8. ↑ Margarete Weninger (1976): Zur polygenen und multifaktoriellen Vererbung. Anthropologischer Anzeiger 35 (4): 236-239. JSTOR 29538872
  9. ↑ Jochen Graw, Wolfgang Hennig: Genetik. 5., vollst. überarb. Auflage. Springer, Berlin/ Heidelberg 2010, ISBN 978-3-642-04998-9, S. 456–459.
  10. ↑ Multifaktorielle (polygene) Vererbung. In: Werner Buselmaier, Gholamali Tariverdian: Humangenetik. 3., aktualis. und neu bearb. Auflage. Springer, 2004, ISBN 3-540-00873-X, S. 226.
  11. ↑ Robert Elston, Jaya Satagopan, Shuying Sun (2012): Genetic Terminology. Methods of Molecular Biology 850: 1–9. doi:10.1007/978-1-61779-555-8_1
  12. ↑ Arnold Lohaus, Marc Vierhaus, Asja Maass: Entwicklungspsychologie des Kindes- und Jugendalters für Bachelor. 1. Auflage. Springer, Berlin/ Heidelberg 2010, ISBN 978-3-642-03935-5, S. 126.
  13. ↑ A.K. Kalla (2007): Human Skin Colour, Its Genetics, Variation and Adaptation: A Review. Anthropologist Special Issue No. 3: 209-214. PDF
  14. ↑ Genetik und Immunbiologie. (Natura). Klett, Stuttgart 1997, ISBN 3-12-042939-2. (Lehrerband)
  15. ↑ vgl. Y.S. Demin: Mendel´s Laws. FAO Corporate Document Repository, abgerufen am 17. Juin 2017.
  16. ↑ Patrick C. Phillips (2008): Epistasis — the essential role of gene interactions in the structure and evolution of genetic systems. Nature Reviews Genetics 9: 855-867. doi:10.1038/nrg2452
  17. ↑ H. Allen Orr (1996): Dobzhansky, Bateson and the Genetics of Speciation. Genetics 144: 1331–1335.

Literatur

  • Jochen Graw, Wolfgang Hennig: Genetik. 5. Auflage. vollst. überarb. Auflage. Springer, Berlin/ Heidelberg 2010, ISBN 978-3-642-04998-9, S. 456–459.
  • Multifaktorielle (polygene) Vererbung. In: Werner Buselmaier, Gholamali Tariverdian: Humangenetik. 3., aktualis. und neu bearb. Auflage. Springer, 2004, ISBN 3-540-00873-X, Kapitel 6.

Weblinks

Abgerufen von „https://de.wikiup.org/index.php?title=Polygenie&oldid=218163802“